The discontinuous nature of dislocation movement

A significant experiment performed by Johnston and Gilman simply involved etching a LiF crystal while it was under a load. This produced the result, shown schematically in Fig.1.3, where an array of etch pits reveals the movement of a small dislocation loop. This loop interested the surface at its two ends. The two largest etch pits with square flat bottoms, at the center of the array, mark the locations of the two ends of the loop at the start of the test. The final positions of these ends correspond to the two small pits with sharp pointed bottoms at the ends of the array. Note that in this array between the starting and final position of the ends of the loop, there are a series of flat-bottomed etch pits that decrease in size as one approaches the final positions of the loop ends. This suggests that the pits were etched for a shorter and shorter time as one moves from the original positions of the loop ends toward their final positions. These pits are easily interpreted as marking stopping points for the dislocation as it moved during the time of application of the load. Accordingly, this experiment demonstrates that the movement of a dislocation is not smooth and continuous, but rather it occurs in steps. In brief, a dislocation moves rapidly for a short distance; it stops and waits at an obstacle which eventually it passes; then it moves rapidly again to the next obstacle. It is now generally believed that thermal vibrations aid the applied stress to overcome these obstacles to dislocation motion. Consequently, the dislocation velocity is better considered as

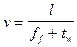1.11

where l is the average distance between obstacles, t_f the time of flight between obstacles, and t_w the average time the dislocation waits at an obstacle for the thermal energy to become large enough to allow the dislocation to penetrate the obstacle.

Fig.1.3. Schematic of Johnston and Gilman’s result obtained by etching during a stress pulse.

Empirical observation strongly support the conclusion that t_w is much longer than t_f so that one may ignore the latter and write

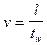1.12

In general t_w depends not only on the temperature but also on the stress. This is in excellent agreement with both the stress dependence of the dislocation velocity expressed in Eq.1.7 and the temperature dependence of the velocity in Eq.1.9.