The dislocation velocity

The work of Johnston and Gilman [9 ] on LiF single crystals added much to our knowledge about the movement of dislocations. The principal advantage of working with LiF crystals was that they were able to introduce controlled, small numbers of dislocations into these crystals and then to observe quantitatively the movements of both screw and edge components of their dislocations. Metal crystals are normally much more difficult to work with, in this regard, because even very small deformations can produce relatively high dislocation densities, thus making it difficult to observe the motions of individual dislocations. The dislocation velocity could be measured by diving the distance moves by the time of application of a stress pulse, i.e. v=d/t, where v is dislocation velocity, d the distance between the each pits marking the original and dislocation positions, and t the time of application of the stress pulse. For a given set of conditions (i.e. temperature, stress level, and time of application of the stress pulse), the distance moved by a statistically significant number of the same type of dislocation were measured and averaged to obtain the dislocation velocity for these conditions.

An interesting observation made by these authors was that in their LiF crystals, a dislocation with an edge orientation would normally move 50 times faster than one with a screw orientation, other things being equal. Johnston and Gilman investigated the dependence of the dislocation velocity on the magnitude of the stress at constant temperature and found that for velocities slower than about 0,1

lnv µ lnt 1.6

which implied the existence of a power law between shear stress and dislocation velocity. Johnston and Gilman expressed this power law in the form

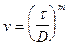1.7

where v is the dislocation velocity, t the applied shear stress, m the dislocation velocity stress exponent, and D the stress that yields a dislocation velocity of 1 cm/s (0,01 m/s).

For some of the LiF crystals tested at room temperature, Johnston and Gilman observed that D=540 gm/mm² (5,3 MPa) and m=16,5. Thus, as an example, a shear stress t of 2,65 MPa should yield a room temperature (300 K) velocity in these crystals of

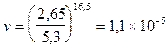cm/s 1.8

The variation of the dislocation velocity with the absolute temperature, at a constant stress, was also investigated by these authors. In this case it was observed that the logarithm of the velocity was proportional to the reciprocal of the absolute temperature or

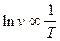1.9

where v is the dislocation velocity and T the absolute temperature. At the time of these observations, Johnston and Gilman proposed that one could write a single expression relating v to both stress and temperature in the form

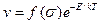(+25⁰C>T>-50⁰C) 1.10

where v is the dislocation velocity, f(s) a factor representing the stress dependence of the dislocation velocity, k Boltzmann’s constant, E an activation energy, and T the absolute temperature.