The relation between dislocation density and the stress

With the development of the transmission electron microscope technique, it has been possible to make direct studies of the dislocation structure in deformed metals. These investigations have indicated that for a very wide range of metals there exists a rather simple relationship between the dislocation density and the flow-stress of a metal. Thus, let us assume that Fig.1.1 represents the general shape of the stress-strain curve of a metal and that a series of specimens are deformed to different strains, as indicated by the marked points along the curve.

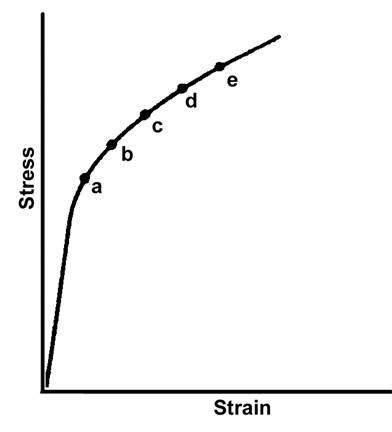Fig.1.1. To determine the variation of the dislocation density with strain during a tensile test, a set of tensile specimens are strained to a number of different positions along the stress-strain curve, such as points a to f in this diagram. These specimens are then sectioned to obtain transmission electron microscope foils.

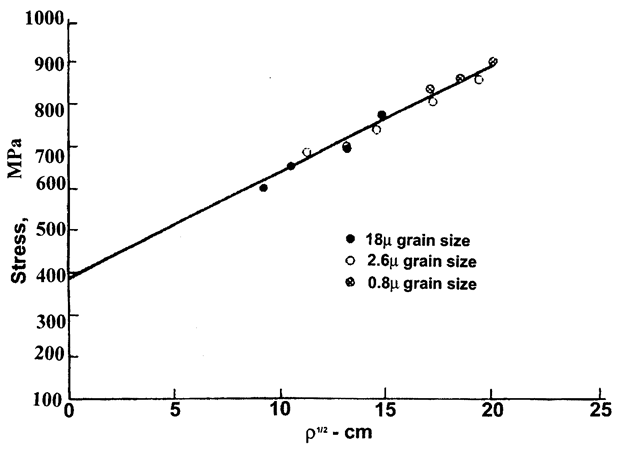Furthermore, let us assume that on reaching the specified strains, they are unloaded, sectioned for observation in the electron microscope, and that dislocation density measurements are made on the foils. Fig.1.2 shows the actual experimental results obtained using a set of titanium specimens.

Fig.1.2. The variation of the flow-stress s with the square root of the dislocation density r^1/2 for titanium specimens deformed at root temperature and at a strain rate of 10^-4 s^-1 [6].

This data corresponds to specimens of three different sizes. Note that all of the data plots on the same straight line. Data such as this supports the assumption that the stress varies directly as the square root of the dislocation density, or

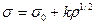1.1

where r is the measured dislocation density in centimeters of dislocation per unit volume, k is a constant, and s₀ is the stress obtained when r^1/2 is extrapolated to zero. This result is good evidence that the work hardening in metals is directly associated with the build-up of the dislocation density in the metal. While the above relationship to data from polycrystalline specimens, the relationship has also been observed in single-crystal specimens. In this case, it is more proper to express the relationship in perms of the resolved stress on the active slip plane t.

This gives us

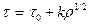1.2

where t₀ is the extrapolated shear stress corresponding to a zero dislocation density. Actually, if the dislocation density were zero, then the metal could not be deformed. As a consequence, s₀ or t₀ are best considered as convenient constants rather than as simple physical properties.

Taylor’s relation

In 1934, Taylor [7] proposed a theoretical relationship that is basically equivalent to the experimentally observed functional relationship between the flow stress and the dislocation density. In the model that he used, it was assumed that all the dislocations moved on parallel slip planes and the dislocations were parallel to each other. This model has since been elaborated by Seeger [8] and his collaborators. In brief, this approach assumes that if the dislocation density is expressed in numbers of dislocations intersecting a unit area, then the average distance between dislocations is proportional to r^1/2 . The stress field of a dislocation varies as 1/r, or in general we may write

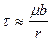1.3

where m is the shear modulus, b is the Burgers vector, and r is the distance from the dislocation. Now consider two edge dislocations on parallel slip planes. If they are of the same sign, they will exert a repulsive force on each other. If they are of opposite sign, the force will be attractive. In either case, this interaction must be overcome in order to allow the dislocations to continue to glide on their respective slip planes. Since, as shows above, the average distance between dislocations is proportional to r^1/2, we have

t = ambr^1/2 1.4

or

t = kr^1/2 1.5

where k is a constant of proportionality equal to amb.