Удаление вершины из Б-дерева

Пусть имеется Б-дерево порядка m, из которого требуется удалить элемент с ключом х. Прежде всего, организуется поиск удаляемого элемента последовательным просмотром страниц, начиная с корневой. Пусть удаляемый элемент найден на некоторой странице. При этом возможны следующие две ситуации:

· если найденная страница является терминальной, то элемент просто удаляется с нее с последующей проверкой количества оставшихся на этой странице элементов; если после удаления на странице остается слишком мало элементов, предпринимаются некоторые дополнительные действия, описываемые немного позже

· если страница нетерминальная, то на место удаляемого элемента надо поставить элемент-заменитель, который находится также, как и в обычном дереве: входим в левое (правое) поддерево и спускаемся как можно ниже, придерживаясь максимально правых (левых) поддеревьев; после этого надо проверить страницу, с которой был взят элемент-заменитель и при необходимости предпринять корректирующие действия для восстановления структуры Б-дерева

Например, пусть в простейшем Б-дереве порядка 2 на рисунке ниже требуется удалить элемент с ключом х = 40. Левое поддерево для ключа 40 определяется ссылкой, связанной с его левым соседом, т.е. элементом 20. Просматриваем новую страницу (26, 35), выбираем самый правый элемент 35 и по его ссылке выходим на страницу (36, 37, 38). На этой странице крайний правый элемент 38 не имеет потомка и поэтому именно он должен быть элементом-заменителем. Ясно, что он является ближайшим меньшим элементом по отношению к удаляемому. Путь к элементу-заменителю показан жирной линией.

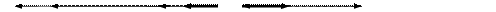
В обоих случаях после удаления элемента с некоторой страницы надо эту страницу проверить на число оставшихся элементов. По правилам построения Б-деревьев на каждой странице (кроме корневой) не может быть меньше m элементов. Если это условие после удаления не выполняется, т.е. на странице остается лишь m-1 элемент, необходима ее корректировка за счет привлечения одной из соседних страниц. Для этого с помощью родительской страницы определяется адрес соседней страницы и выполняется ее загрузка в ОП. Совместная обработка двух соседних страниц выполняется следующим образом.

1. Если на соседней странице имеется более m элементов (хотя бы m+1), то выполняется перераспределение элементов: с более “богатой” соседней страницы некоторое число элементов передается на “бедную” текущую страницу. В простейшем случае достаточно передать один элемент, но на практике чаще всего передается столько элементов, чтобы на этих двух страницах их было почти поровну. Здесь есть один тонкий момент – элементы с одной страницы на другую передаются не прямо, а через родительскую страницу, т.е. происходит как бы перетекание элементов с дочерней страницы на родительскую с вытеснением с нее элементов на текущую страницу.

2. Если соседняя страница сама является “небогатой”, т.е. содержит ровно m элементов, используется другой прием. В этом случае происходит объединение двух “бедных” страниц с созданием одной полной страницы. Полная страница создается следующим образом: m-1 элемент берется с текущей страницы, m - с соседней и один элемент - с родительской страницы. Интересно, что этот прием заимствования одного элемента с родительской страницы позволяет сохранить необходимую структуру Б-дерева, т.к. синхронно на 1 уменьшается число элементов на родительской странице и число страниц-потомков.

Поскольку число элементов на родительской странице уменьшилось, то надо и эту страницу проверить на “бедность”, и, при необходимости, выполнить ее корректировку. Это, в свою очередь, может привести к заимствованию элемента с еще более верхней страницы и т.д. В худшем случае этот процесс распространится до корневой страницы, что может потребовать корректировки самой корневой страницы. Правда, эта корректировка выполняется чуть по-другому, т.к. корневая страница может содержать и меньше m элементов. Особенность возникает лишь тогда, когда до удаления на корневой странице был лишь один элемент, и после удаления она становится пустой. В этом случае эта пустая страница просто удаляется, и тем самым на 1 уменьшается высота Б-дерева.

Пример. Пусть в простейшем Б-дереве порядка 2 удаляется вершина 12 и страница становится “бедной”. Соседняя страница (22, 25, 28) может отдать один элемент, и поэтому ключ 22 передается на родительскую страницу, вытесняя с нее ключ 20.

Если в этом дереве удалить, например, вершину 7, то придется объединять две страницы (5) и (10, 20) вместе и добавлять элемент 8 с родительской страницы для создания одной полной страницы.

Программная реализация удаления имеет те же особенности, что и добавление, т.е. необходимо запоминать траекторию движения от корневой странице к текущей. Для этого можно ввести рекурсивную подпрограмму Delete с тремя параметрами:

· x – ключ удаляемого элемента (параметр-значение)

· pCurrent – ссылка на текущую страницу (параметр-значение)

· IsPure – признак того, что текущая страница после удаления содержит слишком мало элементов (параметр-переменная).

Псевдокод подпрограммы Delete:

procedure Delete (x : <тип ключа>; pCurrent : pPage; var IsPure : boolean);

Begin

if pCurrent = nil then “элемента x в дереве нет”

Else begin

“поиск x на странице pCurrent”;

if “x найден” then

Begin

if “страница pCurrent^ терминальная”

Then begin

“удалить элемент”;

“уменьшить счетчик числа элементов”;

“установить признак IsPure”;

End

Else begin

“найти элемент-заменитель”;

“вставить элемент-заменитель на место удаленного x”;

“уменьшить счетчик числа элементов”;

“установить признак IsPure”;

End

End

Else begin

Delete (x, “адрес дочерней страницы”, IsPure);

if IsPure then “вызов вспом. подпрограммы Pager( )”;

end;

end;

end;

Здесь используется вспомогательная подпрограмма Pager, выполняющая корректировку страницы после удаления с нее элемента x в случае ее “обеднения”. Эта подпрограмма имеет 4 параметра:

· адрес текущей “бедной” страницы (pCurrent)

· адрес родительской страницы (pParent)

· номер элемента на родительской странице, который является непосредственным предком “бедной” страницы (nParent)

· логический признак (IsPure)

Псевдокод подпрограммы Pager:

procedure Pager (pCurrent, pParent : pPage; nParent : integer; var IsPure : boolean);

var pTemp : pPage; {адрес соседней страницы}

Begin

“определение адреса pTemp соседней вершины”;

“определение числа элементов, удаляемых с соседней страницы”;

“пересылка одного элемента с родительской страницы на текущую”;

if “со страницы pTemp пересылается более одного элемента” then

Begin

“пересылка элементов со страницы pTemp на pCurrent”;

“пересылка одного элемента на родительскую страницу”;

“сдвиг влево элементов в массиве на странице pTemp”;

“установка счетчиков числа элементов на соседних страницах”;

IsPure := false;

End

else begin {объединение страниц}

“пересылка всех эл-тов со страницы pTemp на страницу pCurrent”;

“сдвиг влево элементов в массиве на родительской странице”;

“изменение счетчиков числа эл-тов на тек. странице и ее родителе”;

“удаление пустой страницы pTemp”;

“установка признака IsPure для родительской страницы”;

end;

end;

Главная программа должна вызвать подпрограмму Delete, а после возврата из цепочки рекурсивных вызовов – удалить опустевшую корневую страницу.

Внешняя сортировка

Пусть требуется выполнить сортировку сверхбольшого набора данных, который целиком в ОП не помещается. В этом случае рассмотренные ранее методы сортировки массивов не работают и приходится использовать внешние файлы. Исходный набор данных хранится во внешнем файле и, очевидно, многократно должен считываться в ОП. В каждый момент времени в ОП находится лишь часть полного набора. Главным критерием при разработке методов сортировки становится минимизация числа обращений к внешней памяти.

Основой большинства алгоритмов внешней сортировки является принцип слияния двух упорядоченных последовательностей в единый упорядоченный набор.

Например, пусть имеются две упорядоченные числовые последовательности: (5, 11, 17) и (8, 9, 19, 25)

Их слияние выполняется следующим образом:

· сравниваются первые числа 5 и 8, наименьшее (5) помещается в выходной набор: (5)

· сравниваются 11 и 8, наименьшее (8) – в выходной набор: (5, 8)

· сравниваются 11 и 9, наименьшее (9) – в выходной набор: (5, 8, 9)

· сравниваются 11 и 19, наименьшее (11) – в выходной набор: (5, 8, 9, 11)

· сравниваются 17 и 19, наименьшее (17) – в вых. набор: (5, 8, 9, 11, 17)

· остаток второй последовательности (19, 25) просто копируется в выходной набор с получением окончательного результата: (5, 8, 9, 11, 17, 19, 25)

В общем виде алгоритм слияния можно представить следующим образом. Пусть А={a_i} и B={b_j} – две исходные упорядоченные последовательности, R – результирующая последовательность.

1. сравниваем а₁ и b₁, если а₁ < b₁, то записываем а₁ в R, иначе - b₁ в R

2. если в уменьшившемся наборе остались числа, то сравниваем его минимальный элемент с минимальным элементом другого набора и записываем наименьший из них в R

3. повторяем шаг 2 до тех пор, пока не закончится какой-нибудь из наборов

4. как только заканчивается какой-нибудь набор, все оставшиеся элементы другой последовательности копируются в результирующий набор

Алгоритм слияния можно использовать и для сортировки массивов, если последовательно применить его несколько раз ко все более длинным упорядоченным последовательностям. Для этого:

1. в исходном наборе выделяются две подряд идущие возрастающие подпоследовательности (серии)

2. эти подпоследовательности (серии) сливаются в одну более длинную упорядоченную последовательность так, как описано выше

3. шаги 1 и 2 повторяются до тех пор, пока не будет достигнут конец входного набора

4. шаги 1 –3 применяются к новому полученному набору, т.е. выделяются пары серий, которые сливаются в еще более длинные наборы, и.т.д. до тех пор, пока не будет получена единая упорядоченная последовательность.

Пример. Пусть имеется входной неупорядоченный набор чисел:

24, 08, 13, 17, 06, 19, 20, 11, 07, 55, 33, 22, 18, 02, 40

Этап 1. Выделяем в нем серии (показаны скобками) и попарно сливаем их:

(24), (08, 13, 17), (06, 19, 20), (11), (07, 55), (33), (22), (18), (02, 40)

(24) + (08, 13, 17) = (08, 13, 17, 24)

(06, 19, 20) + (11) = (06, 11, 19, 20)

(07, 55) + (33) = (07, 33, 55)

(22) + (18) = (18, 22)

Новый набор чисел:

08, 13, 17, 24, 06, 11, 19, 20, 07, 33, 55, 18, 22, 02, 40

Этап 2. Выделяем в новом наборе серии и попарно сливаем их (число серий уменьшилось):

(08, 13, 17, 24), (06, 11, 19, 20), (07, 33, 55), (18, 22), (02, 40)

(08, 13, 17, 24) + (06, 11, 19, 20) = (06, 08, 11, 13, 17, 19, 20, 24)

(07, 33, 55) + (18, 22) = (07, 18, 22, 33, 55)

Новый набор:

06, 08, 11, 13, 17, 19, 20, 24, 07, 18, 22, 33, 55, 02, 40

Этап 3. Выделяем в новом наборе серии (всего три) и сливаем их:

(06, 08, 11, 13, 17, 19, 20, 24), (07, 18, 22, 33, 55), (02, 40)

(06, 08, 11, 13, 17, 19, 20, 24) + (07, 18, 22, 33, 55) = (06, 07, 08, 11, 13, 17, 18, 19, 20, 22, 24, 33, 55)

Новый набор и его две серии:

(06, 07, 08, 11, 13, 17, 18, 19, 20, 22, 24, 33, 55), (02, 40)

Этап 4. После слияния этих двух серий получим полностью упорядоченный набор:

02, 06, 07, 08, 11, 13, 17, 18, 19, 20, 22, 24, 33, 40, 55

Данный метод сортировки называется естественным слиянием. Его особенностью является то, что для его реализации на каждом шаге достаточно сравнивать только два элемента. Именно это позволяет хранить все основные элементы в дисковых файлах, загружая в ОП только небольшое число элементов из каждой серии.

Алгоритм слияния эффективно работает на длинных сериях и неэффективно на коротких. Поэтому его нецелесообразно применять с самого начала сортировки, поскольку для случайного входного набора на первых шагах будут получаться очень короткие серии, что приведет к неоправданно большому числу обращений к дисковой памяти.

Для устранения этого недостатка можно поступить следующим образом:

· исходный сверхбольшой набор данных разделяется на отдельные фрагменты такого размера, чтобы каждый фрагмент мог целиком разместиться в ОП

· каждый фрагмент отдельно загружается в ОП и сортируется каким-нибудь классическим улучшенным методом (например – алгоритмом быстрой сортировки)

· каждый отсортированный фрагмент рассматривается как серия и сохраняется во вспомогательном файле; в простейшем случае достаточно двух вспомогательных файлов, в которые серии сбрасываются поочередно (нечетные серии – в один файл (A), четные – в другой (B)).

Эти действия носят подготовительный характер.

После этого начинается 2-ой этап сортировки:

· выполняется объединение первых серий из разных файлов, т.е. серий 1 и 2, и результат записывается в третий вспомогательный файл С

· выполняется объединение вторых серий из разных файлов, т.е. серий 3 и 4, и результат записывается во вспомогательный файл D

· выполняется объединение третьих серий из разных файлов, т.е. серий 5 и 6, и результат записывается опять в файл С

· серии 7 и 8 после объединения записываются в файл D и т.д.

В итоге, в файлах С и D получатся объединенные серии, которые потом между собой начинают попарно объединяться с записью результата во вспомогательные файлы А и В и т. д. Процесс укрупнения серий продолжается до тех пор, пока не будет получена одна единственная серия, представляющая полученный результат.

Для программной реализации данного метода сортировки необходимы:

· достаточно большой массив в ОП для реализации 1-го этапа

· пять файлов, из которых один исходный и 4 вспомогательных.

Если необходимой для четырех вспомогательных файлов дисковой памяти не хватает, то можно обойтись двумя вспомогательными файлами, но за счет замедления процесса сортировки. В этом случае объединенные серии из А и В помещаются в исходный файл, а потом распределяются опять в А и В. Тем самым появляется дополнительный шаг распределения серий из исходного файла по двум вспомогательным.

Наоборот, если требуется ускорить сортировку за счет дополнительной дисковой памяти, то вместо 4-х вспомогательных файлов можно использовать 6,8,10 и т.д. Ускорение работы происходит за счет того, что объединяются не 2 серии, а 3, 4 или 5 и т.д.