Оптимізація необхідної і достатньої сукупності параметрів та програми оцінки технічного стану електронного обладнання під час функціонально-логічного моделювання

План лекції

1. Методика визначення необхідної і достатньої сукупності контрольних параметрів.

2. Методологія побудови матриці множин станів об’єкту контролю.

3. Методика визначення сукупності параметрів, які складають мінімальний контрольний тест.

Рівень ефективності процесу оцінки технічного стану електронної апаратури залежить від ступеня оптимального вирішення двох задач: визначення необхідної і достатньої сукупності параметрів контролю та розроблення раціональної програми оцінки технічного стану. Вирішення поставлених завдань здійснюється за допомогою функціонально-логічної моделі ЕА як об’єкта оцінки технічного стану [7]. Методика побудови ФЛМ викладена в матеріалах лекції 11.

Для вирішення цих завдань введемо початкові умови. Нехай ФЛМ об’єкта оцінки технічного стану складається із 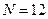структурних елементів. Формуємо обмежувальні умови: в об’єкті одночасно відмовляє тільки один блок (елемент ФЛМ) і ця така відмова елемента призводить до відмови об’єкта в цілому.

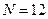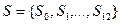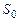Оскільки , то маємо , де – справний стан об’єкта; 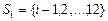– несправні стани, кожний з яких містить у собі одинарну відмову, тобто відмову тільки одного з елементів об’єкта. Враховуючи зазначене, представимо матрицю множини станів об’єкта (таблиця 12.1).

В табл. 11.1 наведено: 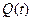– імовірність виникнення стану 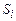у разі відмови відповідного елемента (блоку) об’єкта; 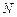– порядковий номер станів.

Під елементарною перевіркою 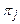будемо розуміти процедуру вимірювання вхідних і вихідних сигналів тільки одного із елементів ФЛМ.

Позначимо результат перевірки 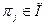( 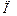– множина всіх елементарних перевірок) через 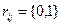. Тоді, 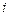-й рядок табл. 12.1 можна подати у вигляді попарного набору

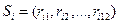, (12.1)

де .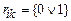

Таблиця 12.1

Матриця множини станів об’єкта

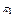
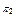
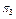
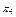
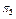
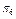
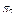
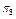
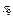
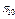
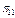
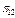
S													Q(t)
S0
S1													0,12
S2													0,51
S3													0,50
S4													0,72
S5													0,62
S6													0,43
S7													0,38
S8													0,81
S9													0,70
S10													0,67
S11													0,24
S12													0,32

Стани 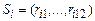та 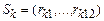називають попарно відмінними за множиною 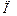, якщо результати хоча б однієї перевірки цих станів не співпадають (наприклад, 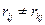). Відмінність станів позначається як 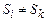. Позначимо через 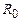множину невпорядкованих пар виду 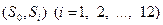, а через 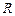– множину невпорядкованих пар виду 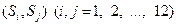, до того ж пари 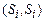вилучаються з розгляду.

Використовуючи матрицю множини станів об’єкта (табл. 12.1), можна визначити оптимальну сукупність перевірок 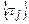як для контролю працездатності (контролюючий тест 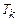), так і для локалізації відмов (діагностичний тест 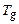). Визначення параметрів 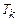і 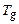можна здійснити двома засобами: аналітичним, використовуючи метод булевих перетворень Мак-Класки, або експериментальним, використовуючи алгоритм булевих спрощень Яблонського. У процесі викладення матеріалу основну увагу буде приділено застосуванню алгоритму Яблонського.

Множина перевірок 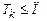називається контролюючим тестом, за умови, якщо, які б не були пари 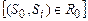,то буде мати місце сукупність різних станів 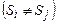на множині 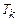. Проведення перевірок, які входять до тесту 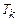, дозволяє виявити справний або несправний стан будь-якого блоку системи, тому такий тест носить назву контролюючий.

Множина перевірок 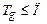називається діагностичним тестом, якщо які б не були пари 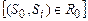, можна розпізнати будь-який стан із множини несправних станів, до яких привели відмови в об’єкті контролю. За допомогою перевірок, які входять в діагностичний тест, можна здійснити локалізацію ФЕ, який відмовив.

Тести 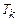і 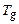, які вміщують мінімальну кількість перевірок називаються мінімальними. Визначити мінімальний тест – це означає знайти мінімальну кількість параметрів (виходів блоків), достатніх для здійснення контролю працездатності об’єкта ( 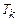) або локалізації відмов ( 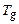), які можуть у ньому виникати.

Зупинимося більш детально на вирішенні завдання визначення і мінімізації контролюючого тесту 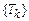. Якщо мінімальний тест виявиться єдиним, то кількість перевірок, яку він містить, буде не тільки достатньою, але й необхідною для оцінки працездатного стану об’єкту контролю.

Для кожної пари 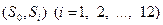визначимо дискретний набір

,

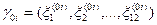де

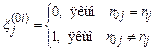. (12.2)

Одиниці в наборі 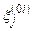характеризують ті перевірки, за яких стани та 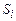відрізняються. На основі інформації із матриці станів (табл. 12.1), а також враховуючи (12.2), побудуємо булеву матрицю 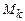(табл. 12.2), рядками якої є набори 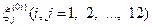, а колонками – сукупність перевірок .

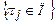Таблиця 12.2

Матриця 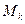працездатності об’єкта

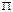S

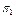
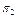
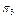
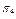
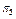
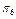
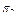
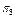
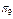
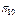
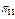
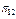
S0 S1

S0 S2

S0 S3

S0 S4

S0 S5

S0 S6

S0 S7

S0 S8

S0 S9

S0 S10

S0 S11

S0 S12

Для визначення оптимальної сукупності перевірок контролюючого тесту із застосуванням методу булевих перетворювань необхідно для матриці 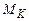описати аналітичний взаємозв’язок між сукупністю перевірок 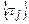і множиною станів 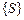. Для цього формується булева функція диз’юнкція-кон’юнкцій станів 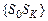і сукупності перевірок :

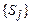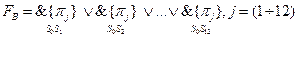. (12.3)

Сутність аналітичного вирішення рівняння (12.3) полягає у булевому перетворенні диз’юнкції-кон’юнкції в кон’юнкцію-диз’юнкцій. В результаті таких перетворень можна отримати мінімальну сукупність 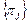, яка утворює оптимальний контролюючий тест 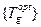. Але процедура аналітичних перетворювань достатньо складна. У зв’язку з цим на практиці застосовують спрощену методику аналізу матриці 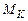з метою отримання раціонального (близькому до мінімального) контрольного тесту .

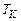Застосовуючи алгоритм булевих спрощень, визначимо мінімальну сукупність перевірок 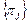, які утворюють раціональний контролюючий тест .

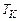Для матриці 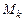застосуємо процедуру спрощення за таким алгоритмом:

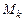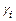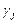а) якщо в матриці є така пара рядків і , що 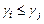, то рядок 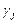з неї вилучається (вважається 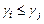, якщо для всіх );

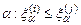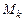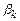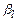б) якщо в матриці є така пара колонок та , що 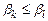, то колонка 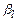з неї вилучається.

в) Якщо в матриці 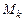є рядок, який вміщує тільки одну одиницю, яка стоїть на перетині 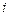-го рядка та 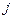-ї колонки, то перевірка 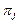, що відповідає 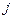-й колонці, входить до мінімального тесту. Якщо після спрощення матриці 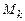за правилами 1 та 2 в ній залишаються тільки перевірки, які входять до мінімального тесту, то сукупність цих перевірок складає мінімальний контрольний тест .

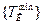В результаті зазначених процедур спрощення із матриці 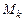утворюється нова матриця 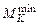(табл. 12.3), стовпці якої вміщують сукупність перевірок мінімального контролюючого тесту .

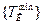Із порівняльного аналізу матриць 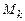і 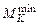випливає, що в результаті застосування методики булевих спрощень із 12 перевірок у мінімальний контролюючий тест увійшло 8 перевірок, необхідних і достатніх для оцінки технічного стану кожного окремого блока системи, яка перевіряється.

Визначивши мінімальну сукупність перевірок 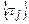, можна розробити ефективний алгоритм (програму) реалізації процесу контролю працездатності на рівні системи, яка складається із певної множини блоків. Необхідно зазначити, що реалізація такої процедури контролю дозволяє на структурному рівні здійснити попереднє діагностування системи (з глибиною до змінного конструктивного блоку).

Таблиця 12.3

Матриця 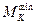програми оцінки технічного стану об’єкта

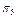
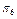
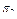
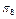
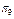
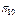
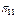
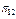
№ п/п									С(грн.)	R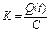
											0,008
											0,063
											0,050
											0,180
											0,088
											0,047
											0,034
											0,405
											0,140
											0,111
											0,017
											0,026

Згідно з табл. 12.3 мінімальна сукупність параметрів визначена як

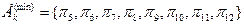. (12.4)

Концептуальні основи побудови зазначеної програми полягають в наступному. З табл. 12.1 використовуються дані щодо імовірності 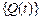появи одного із 12 станів у разі відмови відповідного блока системи. Як відомо, роботи з реалізації кожної із перевірок оцінюються певним рівнем вартості С (табл. 12.3). Для того, щоб з’ясувати, з якого апріорно визначеного стану (табл. 12.3) розпочати процес контролю, із таблиці 1 вибирається стан 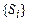з максимальним значенням 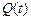(для табл. 12.1 таким станом є 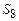), а з таблиць 2 і 3 знаходиться порядковий номер і значення стану 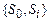, для якого вартість робіт з контролю має найменше значення. В табл. 12.3 найменша вартість має сполучення 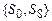. В результаті розраховується значення 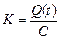. Отже першим кроком R в програмі контролю буде той, для якого значення К максимальне. В цьому прикладі програма контролю повинна починатися зі стану, відповідає 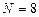. Аналізуючи значення К із табл. 12.3 етапи ефективної програми мають таку послідовність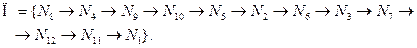

Методика розрахунків значень {С} детально викладена в матеріалах лекції 18.

Контрольні питання

1. Поясніть, в чому полягає сутність оптимізації необхідної і достатньої сукупності параметрів контролю?

2. Розкажіть, яка послідовність (алгоритм) побудови матриці множини станів об’єкту контролю?

3. Поясніть, як використовується алгоритм булевих спрощень під час визначення контрольного тесту?

Література – [7].