Колебание трехмерной решетки

Результаты, полученные для линейной цепочки атомов, могут быть обобщены на случай трехмерного кристалла, который представляет собой систему из большого количества связанных между собой атомов. Из теории колебаний известно, что такая система может быть описана независимыми простыми колебаниями, которые называются нормальными колебаниями или модами системы. Каждая нормальная мода описывает колебание всей кристаллической решетки, то есть всех атомов, но математически выглядит как колебание простого осциллятора.

В случае кристаллов с примитивной решеткой Браве, которая содержат в элементарной ячейке лишь один атом, существуют только акустические колебания, как и для линейной цепочки, состоящей из атомов одного сорта. При этом каждому вектору 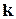отвечает одно продольное и два поперечных колебания, а всего в коллективе из 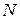атомов может существовать 3 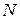колебаний.В трехмерных кристаллах с многоатомным базисом может существовать 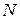продольных акустических колебаний, 2 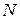поперечных акустических колебаний, 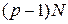продольных оптических и 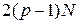поперечных оптических колебаний. Здесь р – число атомов в базисе, 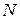– число базисных групп в кристалле. Следовательно, кристаллы с многоатомным базисом имеют очень сложный спектр колебаний.

Определим спектр нормальных колебаний решетки, ограничившись для простоты примитивной решеткой Браве, в которой могут возникать только акустические колебания. Для этого представим кристалл в виде куба с ребром 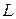. Используя так называемые периодические граничные условия, получим возможные значения составляющих вектора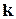

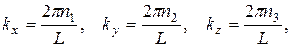(3.12)

где n₁, n₂, n₃ – любые целые числа. Следовательно, на одно состояние в 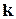– пространстве приходится объем 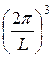. Тогда в шаровом слое толщиной 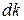будет находиться состояний

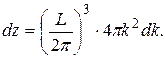(3.13)

Переходя к частотам, получим (без учета дисперсии)

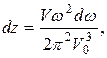(3.14)

где 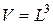– объем кристалла, 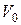– скорость звука.

Необходимо учесть, что на одно продольное колебание приходится два поперечных колебания. Тогда плотность заполнения спектрального участка нормальными колебаниями определится следующим выражением

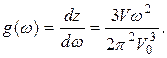(3.15)

Величина 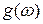называется функцией распределения нормальных колебаний (плотностью состояний).

Так как в кристалле, содержащем 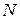атомов, число акустических колебаний равняется 3 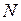, функция 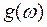должна удовлетворять следующему условию нормировки

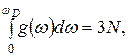(3.16)

где w_D – максимальная частота, которая ограничивает спектр нормальных колебаний сверху.

Подставив (3.15) в (3.16) и проинтегрировав, определим w_D

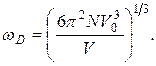(3.17)

Частота w_D называется характеристической дебаевской частотой, а температура

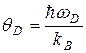(3.18)

называется характеристической температурой Дебая[2]. Здесь k_B – постоянная Больцмана.

Используя выражение (3.17), преобразуем формулу для спектральной плотности (3.15) к следующему удобному виду

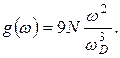(3.19)

Фононы

Каждое нормальное колебание несет с собой порцию энергии и импульса. Полная энергия кристалла, который состоит из атомов, совершающих связанные колебания, может быть представлена в виде энергии независимых нормальных гармонических осцилляторов. Из квантовой механики известно, что энергия квантового осциллятора дискретна. Поэтому должна квантоваться и энергия нормальных колебаний решетки. Такой квант энергии нормального колебания назвали фононом по аналогии со световым квантом – фотоном. Фонон имеет энергию и импульс

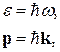(3.20)

а его скорость определяется групповой скоростью распространения колебаний .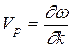

Фононы во многих случаях ведут себя как настоящие частицы: в процессах обмена энергией (рождается и исчезает целое число фононов), при рассеянии на дефектах решетки и т.д. Однако фононы не являются частицами в обычном смысле. Они представляют корпускулярный способ описания коллективных волновых движений в кристалле и существуют лишь постольку, поскольку существует сам упорядоченный коллектив атомов. Фононы не могут быть выведены из кристалла и исчезают вместе с разрушением кристалла.

Фононы играют большую роль в протекании многих явлений в кристалле. Установление равновесной концентрации носителей заряда происходит путем взаимодействия их с фононами. Они определяют электрическое сопротивление беспримесных проводников, будучи эффективными центрами рассеяния электронов. Рассеяние фононов друг на друге определяет тепловое сопротивление решетки.

Определим концентрацию фононов. Для этого предварительно найдем число фононов в интервале 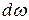. Оно будет равняться произведению числа состояний 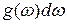на вероятность заполнения этих состояний 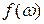. Фононы представляют собой бозе-частицы со спином равным нулю (в единицах 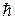), поэтому функция 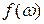является распределением Бозе[3]-Эйнштейна[4]:

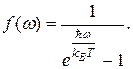(3.21)

Разделив полученное произведение на объем кристалла V, получим число фононов в единице объема в интервале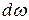

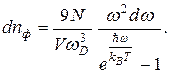(3.22)

Проведя интегрирование по всем возможным частотам от 0 до 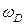, найдем концентрацию фононного газа

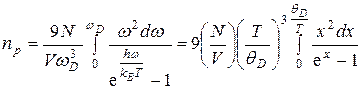, (3.23)

где введена переменная .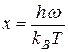

В области низких температур ( 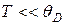) верхнюю границу интегрирования заменяем бесконечностью и, учитывая что

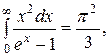(3.24)

получим концентрацию фононов

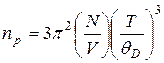. (3.25)

В области высоких температур ( )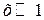

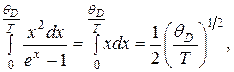(3.26)

и концентрация фононов оказывается пропорциональной температуре

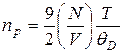. (3.27)

Характеристическая температура Дебая. Тепловые колебания атомов решетки носят качественно различный характер в двух температурных областях, обусловленный соотношением между энергией связи в твердом теле U_св и энергией тепловых колебаний атома k_BT.

В области высоких температур ( 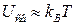) атомы колеблются возле положения равновесия со случайными фазами (не согласовано), что приводит к отсутствию "мгновенной" периодичности кристаллической решетки. Это обстоятельство существенно лишь для быстрых процессов, длительность которых меньше периода колебаний атомов ( 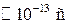). Однако для процессов с характерным временем 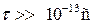происходит усреднение смещения атомов из положения равновесия, и решетку можно рассматривать как периодическую.

По мере снижения температуры устанавливается корреляция между движением отдельных атомов, что приводит к согласованности их колебаний. И в области низких температур ( 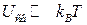) энергия связи атомов настолько велика по сравнению с энергией тепловых колебаний, что атом при своем смещении захватывает в том же направлении соседние атомы и это приводит к согласованности их движения. Эта картина аналогична возникающей при распространении звуковой волны в твердом теле. В этой области температур твердое тело можно рассматривать как непрерывную среду.

Температура, которая условно разделяет две температурные области, качественно различные по характеру тепловых колебаний атомов, называется характеристической температурой Дебая q_D.

Типичные значения q_D для некоторых веществ приведены в таблице 3.1

Таблица 3.1. Температура Дебая некоторых кристаллов

Температура Дебая является очень удобным физическим параметром, так она входит во многие теоретически определяемые физические характеристики различных явлений, в том числе в теплоемкость, теплопроводность, электрическое сопротивление и др.