ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ
Границы участков, площади которых необходимо определить на плане или карте, могут иметь прямолинейное или произвольное очертание.
При прямолинейных очертаниях определение площади возможно двумя способами:
1. Геометрический (графический) - по расчетным формулам конкретных геометрических фигур;
2. Аналитический - по координатам вершин углов многоугольника.
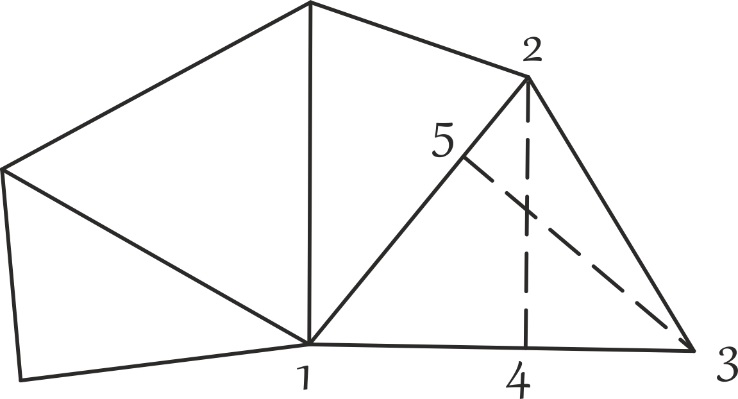
Рис. 21. Геометрический способ определения площадей
В первом случае участок разбивают преимущественно на треугольники, реже на прямоугольники и трапеции (рис. 21). Измеряют линейные элементы (стороны, высоты) и по формулам геометрии вычисляют площади каждой фигуры. Для контроля площади вычисляют дважды, меняя измеряемые элементы. Например, в треугольнике 1–2–3 в одном случае измеряют основание 1–2 и высоту 3–5, в другом – основание 1–3 и высоту 2–4. Расхождение между двумя значениями площадей не должно превосходить 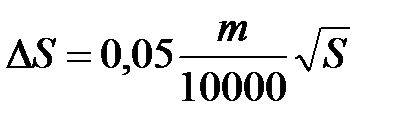 [га], где m – знаменатель численного масштаба. Точность определения площадей примерно
[га], где m – знаменатель численного масштаба. Точность определения площадей примерно 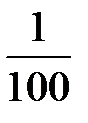 измеряемой величины.
измеряемой величины.
Вычисление площади аналитическим способом, по координатам вершин углов многоугольника, обеспечивает более высокую точность (до 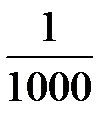 измеряемой величины).
измеряемой величины).
Расчетная формула для определения площади многоугольника (в простейшем случае треугольника – рис. 22):
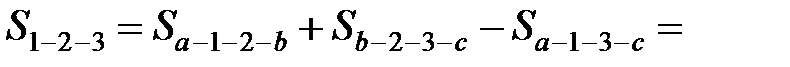
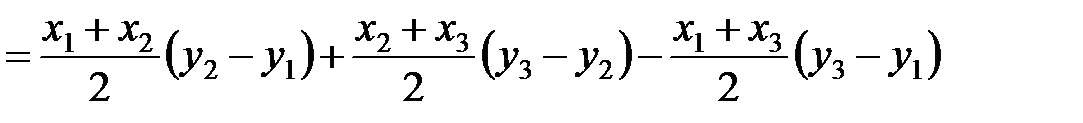 .
.
Произведя соответствующие алгебраические действия и преобразования, получим расчетные формулы:
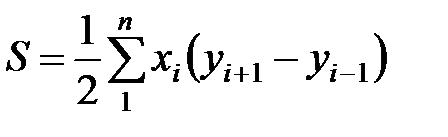 ;
; 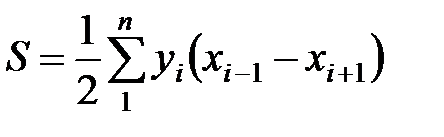 ,
,
где i = 1, 2, 3 ... – номера вершин полигона; 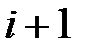 – номер последующей вершины;
– номер последующей вершины; 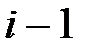 – номер предыдущей вершины.
– номер предыдущей вершины.
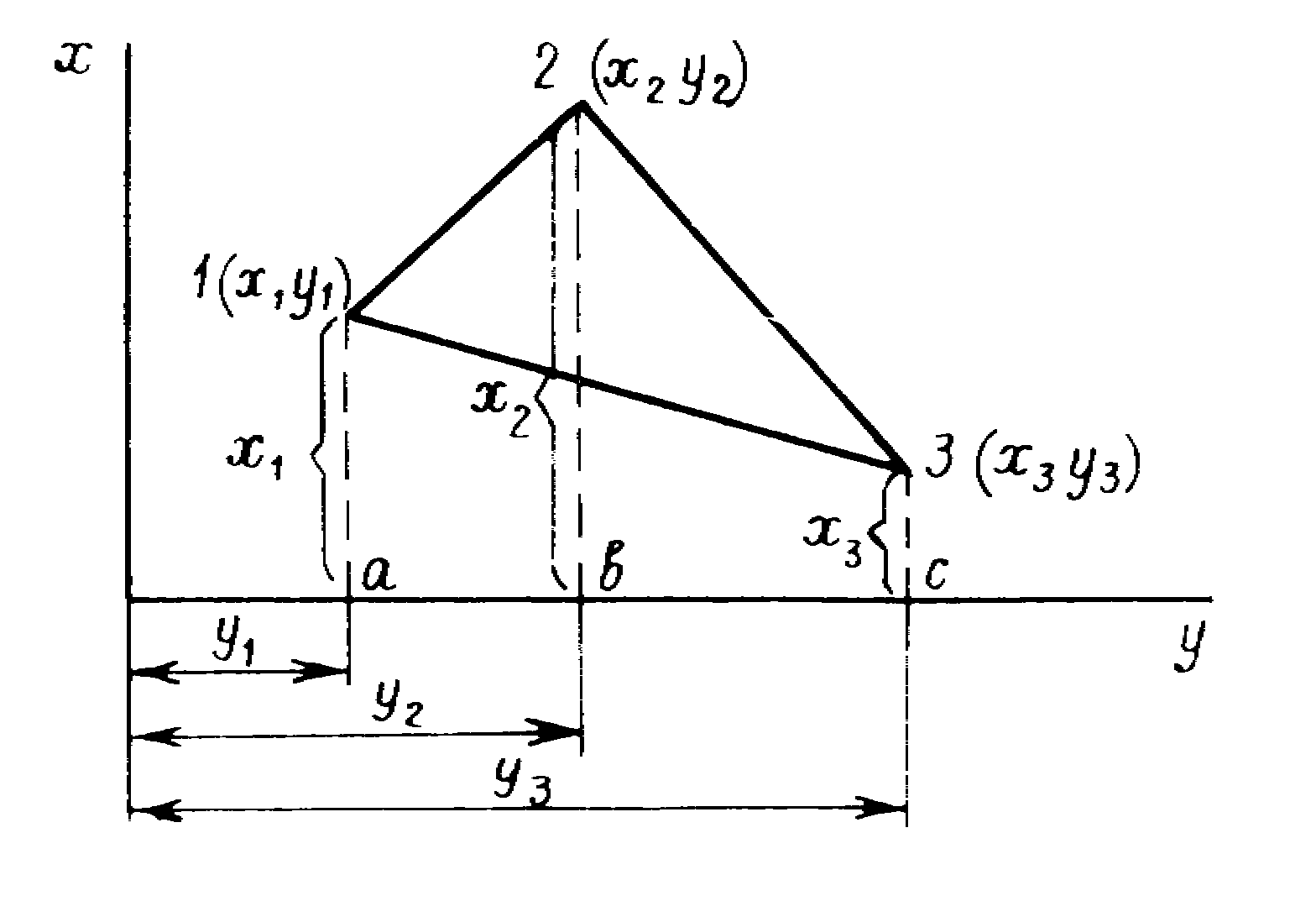
Рис. 22. Аналитический способ
При произвольных очертаниях границ участков определение площади возможно также двумя способами:
- Графический (способ палеток).
Для определения площадей небольших участков с криволинейными контурами (лес, озеро, болото и т.д.) применяют палетки (рис. 23):
– квадратная;
– линейная (параллельная);
– точечная;
– с равностоящими точками.
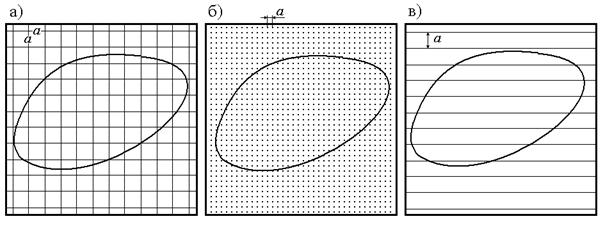
| Рис. 23. а) квадратная палетка, б) точечная палетка, в) линейная палетка |
Палетки изготавливают из кальки размером 15*15 см, расстояние между линиями 2 мм.
Квадратная палетка.Кальку необходимо поделить на квадраты через каждые 2 мм. Квадраты получаются 2х2 мм, т.е. 4 мм2. Затем кальку нужно наложить на топографическую карту, и обвести контур леса. Далее на кальке необходимо сосчитать полные квадраты (например 15) и неполные (например 22, 22: 2= 11 квадратов). х1 = 15 + 11 = 26 мм2.
Эту же кальку повторно накладывают на топографическую карту перевернув и обводят контур леса. Затем считают полные и неполные квадраты (х2).
Далее необходимо определить ошибку (f).
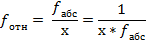
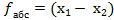
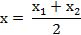
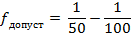
Если полученный результат больше f доп, то необходимо выполнить все измерения и расчеты заново.
Линейная палетка (параллельная).Проводят на кальке параллельные линии через каждые 2 мм. Накладывают кальку на топографическую карту, обводят контур леса таким образом, чтобы границы леса не совпадали с параллельными линиями. Далее необходимо найти сумму внутренних линий. Площадь леса находят по формуле:
S = с*h,
где с – средняя линия (сумма линий внутри контура леса), h – высота.
Эту же кальку повторно накладывают на топографическую карту перевернув и обводят контур леса. Затем находят сумму линий внутри контура леса и по формуле находят х2.
Далее необходимо определить ошибку (f).
Если полученный результат больше f доп, то необходимо выполнить все измерения и расчеты заново.
Точечная палетка.Кальку необходимо поделить на квадраты через каждые 2 мм. Квадраты получаются 2х2 мм, т.е. 4 мм2. В точках пересечения линий обозначить нужно точки. Затем кальку нужно наложить на топографическую карту, и обвести контур леса. Далее на кальке необходимо сосчитать точки, которые находятся внутри контура леса (например 9*4=36 мм2, 4 – вес одной точки).
S = n*с,
где с – вес одной точки, n – количество точек.
Эту же кальку повторно накладывают на топографическую карту перевернув и обводят контур леса. Затем считают точки и находят х2.
Далее необходимо определить ошибку (f).
Палетка с равностоящими точками.Создается на базе квадратной палетки с добавлением еще одной точки на месте пересечения диагоналей.
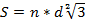 ,
,
где d – расстояние между соседними точками, n – количество точек.
- Механический (с помощью планиметра).
При механическом способе применяют планиметры различных конструкций.
Устройство и поверки планиметра. Полярный планиметр (рис.24) состоит из трех частей: полюсного 1 и обводного 2 рычагов и каретки счетного механизма. Полюсный рычаг с одной стороны имеет груз с иглой 3; перед началом измерений иглу вдавливают в бумагу. С другой стороны полюсный рычаг заканчивается шарниром 6. На конце обводного рычага имеется обводный шпиль 7, которым обводят контур участка, удерживая рычаг за ручку 8. Для того чтобы шпиль не царапал карту, существует штифт 9. На обводном рычаге расположена каретка со счетным механизмом (рис.25). Он состоит из счетного колеса 12, счетчика целых оборотов счетного колеса 13 и верньера 14. При измерении площади участка ободок счетного колеса 15 и ролик 16 должны находиться в пределах листа карты.
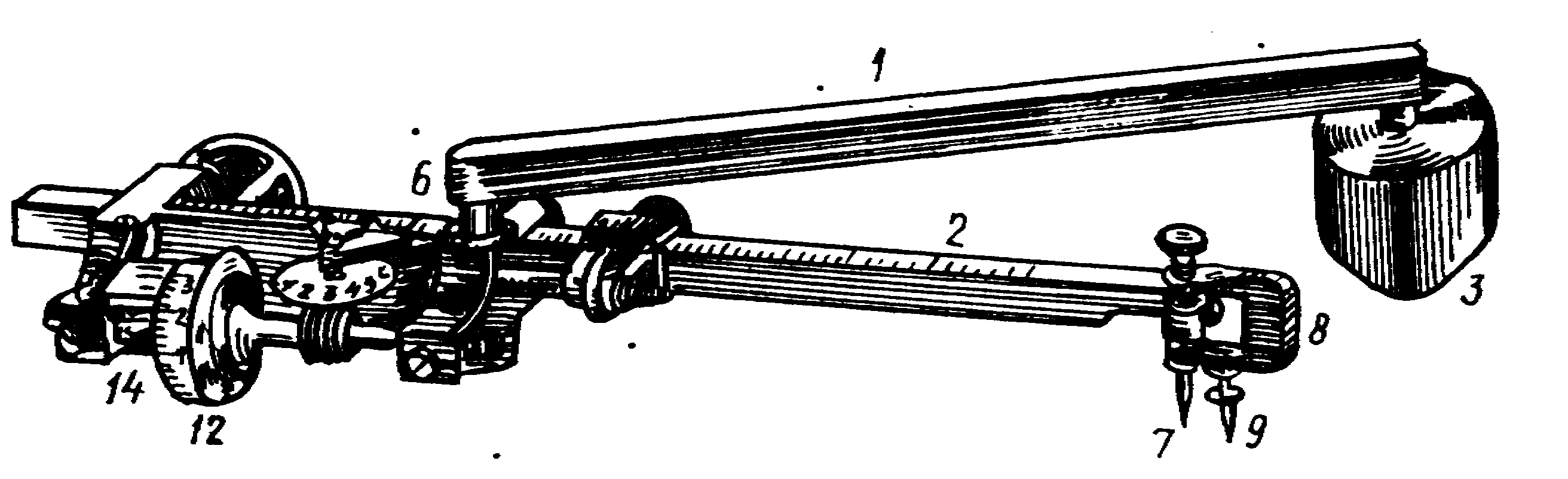
Рис. 24. Полярный планиметр
Счетное колесо разделено на 100 делений, каждые 10 делений оцифрованы. Десятые доли делений счетного колеса определяются по верньеру. Делением планиметра называется одна тысячная часть окружности счетного колеса.
Отсчет по планиметру всегда состоит из четырех цифр. Первая цифра – ближайшая к указателю меньшая цифра счетчика оборотов 13, вторая и третья цифры – сотни и десятки делений на счетном колесе, предшествующих указателю верньера 14 (начальному штриху шкалы верньера, т.е. 0); четвертая цифра – номер штриха верньера, совпадающего с каким-либо штрихом счетного колеса (единицы делений). На рис. 25 отсчет по счетному механизму составляет 3578.
Измерение площадей планиметром. Необходимо знать его цену деления и постоянное значение величины q. Если эти величины неизвестны, то их можно определить.
Цена деления планиметра – это площадь, соответствующая изменению отсчета на одно деление. Геометрически ее можно представить как площадь прямоугольника, одна из сторон которого равна длине обводного рычага, а другая – делению планиметра.
Цену деления можно выразить в мм2, гектарах. Для определения цены деления планиметра берется участок, площадь которого заранее известна, затем производится измерение указанной площади планиметром.
Обводный шпиль сначала устанавливают в центре квадрата, а полюс закрепляют в такой точке, чтобы угол между обводным и полюсным рычагом был равен примерно 90° и чтобы при обводе квадрата ни одна из опорных точек планиметра не выходила за пределы листа карты. Обводный шпиль подводят к одному из углов квадрата и снимают отсчет u1. Далее шпилем обводят стороны квадрата по ходу часовой стрелки. Возвратившись в исходную точку, снимают второй отсчет u2.
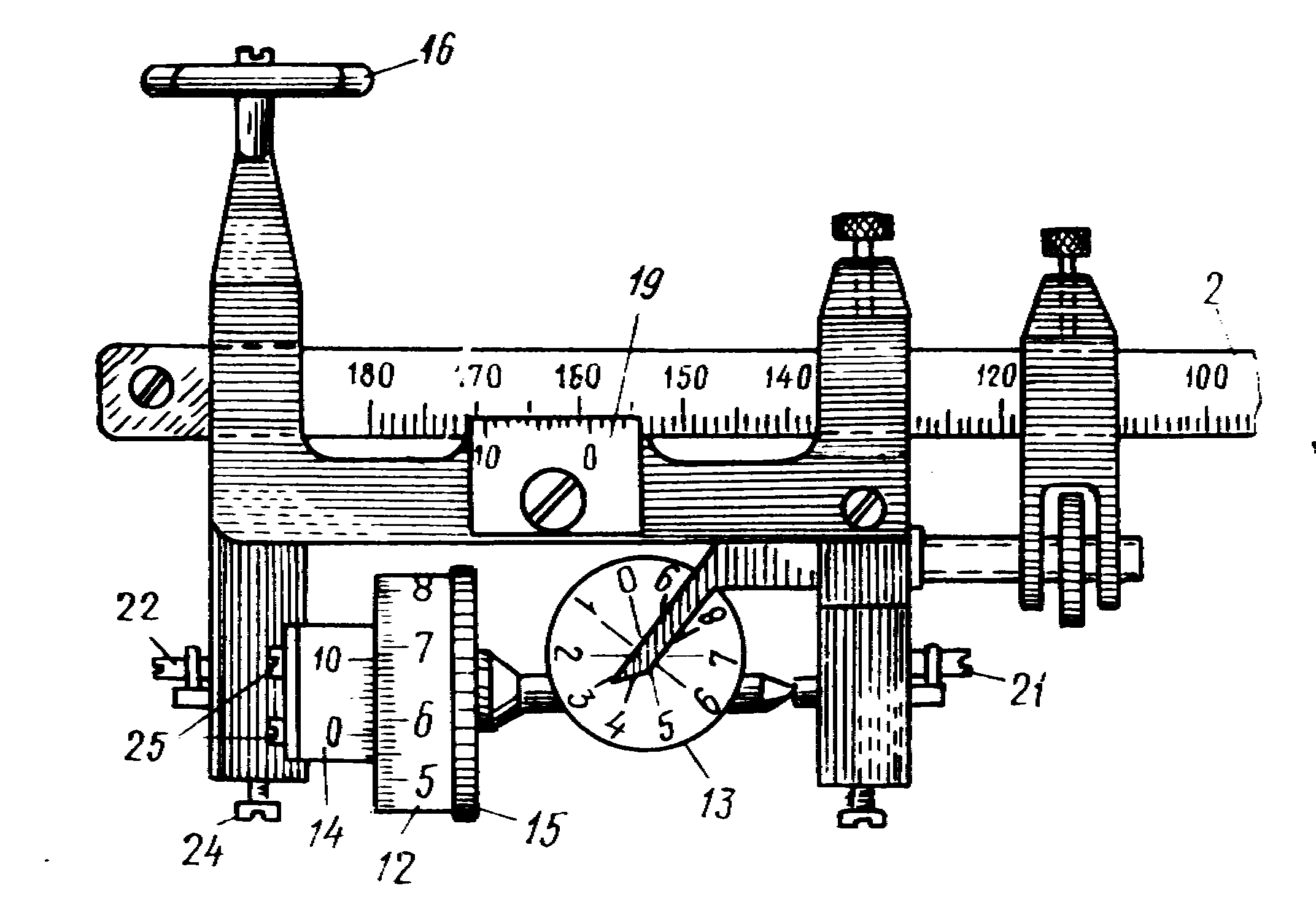
Рис. 25. Взятие отсчета по полярному планиметру
Сместив несколько обводное колесо, вторично производят обвод квадрата против часовой стрелки. При движении по ходу часовой стрелки отсчеты будут возрастать, против часовой стрелки – уменьшаться. Вычитая из большего значения меньшее, находят разности отсчетов, которые не должны отличаться более чем на 5 делений. Проведенные измерения составляют один полуприем. Второй полуприем выполняют в положении полюса с другой стороны обводного рычага и каретки счетного механизма. Расхождение в средних разностях отсчетов при двух полуприемах не должно превышать 5 делений. При наличии сходимости за окончательное значение разности отсчетов принимается среднее из двух результатов.
Цена деления планиметра вычисляется по формуле: 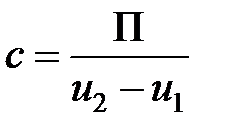 ,
,
где П – площадь измеренного участка; и2 – и1 – средняя разность отсчетов из двух полуприемов.
Измерение площадей относительно небольших участков (в поперечнике не более 15–17 см) производится с полюсом вне контура. Так же, как и при определении с, шпиль располагают примерно в центре участка, а для полюса выбирают такое место, чтобы рычаги планиметра составляли прямой угол (рис. 26 a). Затем производится беглый обвод контура. Угол между рычагами (рис. 26 б, в)должен составлять не менее 30° и не более 150°. Если это условие не выполняется, то подбирается другое, более благоприятное положение полюса. Возможны случаи, когда это не удается, и угол между рычагами выходит за пределы допуска при любом положении полюса. Тогда измерение площадей следует выполнять с полюсом внутри контура (рис. 18,г)или по частям.
Измерение площади участка производится полным приемом, так же как при определении цены деления планиметра.
Расхождения разностей отсчетов в полуприемах допускаются не более 3–4 делений при величине разностей до 1000 делений и 5–6 делений для участков большего размера.
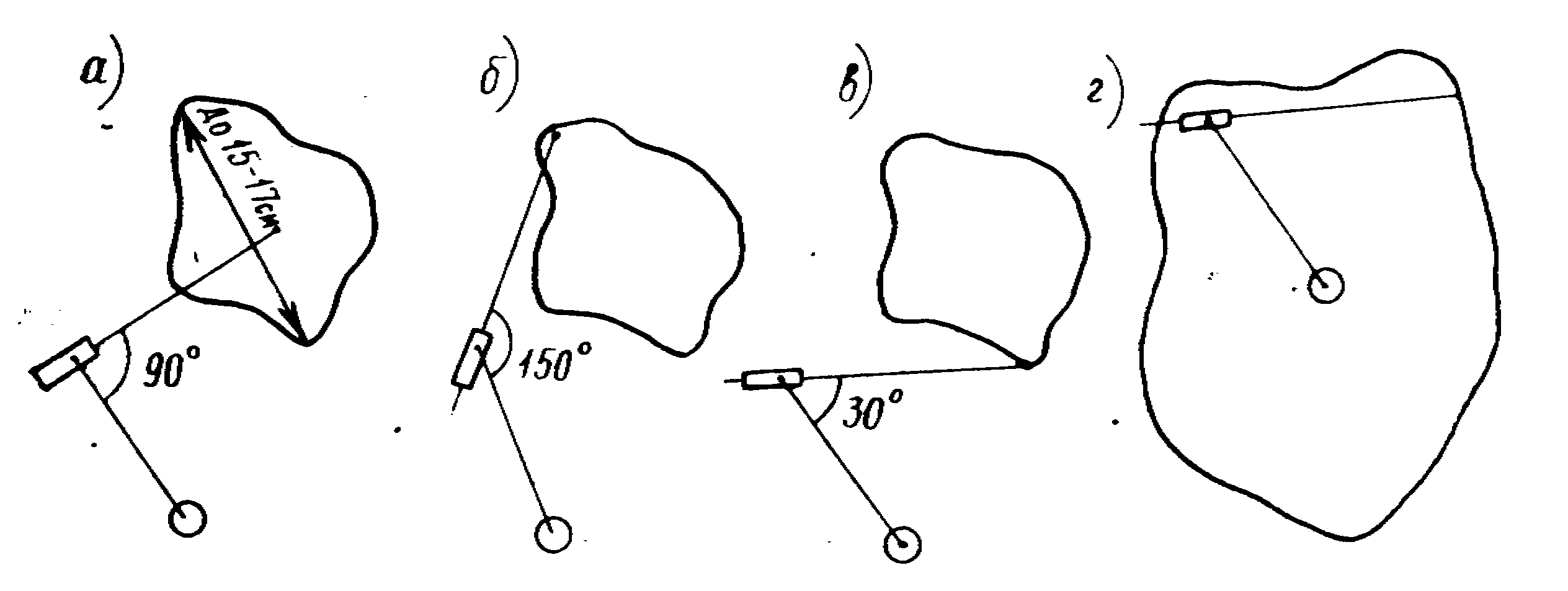
Рис. 26. Измерение площади с помощью полярного планиметра
Площадь участка, измеренная при полюсе вне контура, вычисляется по формуле: 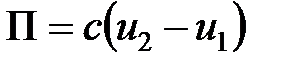 .
.
Значение q планиметра, необходимое при работе с полюсом внутри контура, определяется так же, как и цена деления с,путем обвода контура участка, площадь которого известна. Участок выбирается значительно больших размеров (квадрат 40 ´ 40 см или круг радиусом 30 см). Значение q находится с учетом ранее установленной цены деления с 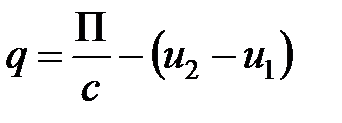 .
.
Площадь с полюсом внутри контура определяется одним приемом и к разности отсчетов добавляется q: П = с(и2 – u1 + q).
Точность результатов измерений планиметром зависит от многих факторов: точности определения постоянных с и q, конфигурации участка, состояния прибора, деформации бумаги и т. д.
Ошибка определения площади находится приближенно по формуле
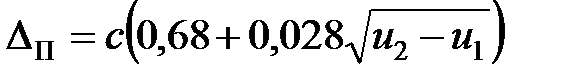 .
.
В настоящее время имеются и электронные планиметры с индикацией результата измерений на экране дисплея.
Планиметр роликового типа PLANIX 7 (рис.27) имеет ролики, обеспечивающие значительное горизонтальное перемещение. Цифровая клавиатура позволяет вводить пользовательский масштаб, в котором вычисляется площадь плана или рисунка.

Рис. 27. Планиметр PLANIX 7
Таблица 5
Основные характеристики планиметра PLANIX 7
| Тип | роликовый |
| Питание | NiCd аккумулятор/блок питания |
| Время работы, ч | |
| Дисплей | 1-строчный 8-ми разрядный ЖК дисплей |
| Точность,% | 0,2 |
| Диапазон измерений | 300 х 30 см |
| Вес, г | |
| Размер, мм | 150 х 240 х 5 |
Дата добавления: 2016-07-11; просмотров: 11780;











