Волновая теория строения атома
Основные положения
Современная теория строения атома была впервые предложена австрийским физиком Э. Шредингером (1925–1926), который объединил в едином волновом уравнении описание движения электрона как частицы с его описанием в виде волны. Уравнение Шредингера – фундаментальное уравнение квантовой механики. Оно описывает движение электронов в атоме с учетом их двойственной природы:
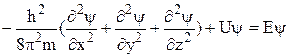 ,
,
где h – постоянная Планка; m – масса электрона; Е – его полная энергия; U – потенциальная энергия, x, y, z – координаты; ψ – волновая функция электрона – амплитуда его волнового движения в трёхмерном пространстве.
При решении уравнения Шредингера находят энергию электрона и его волновую функцию ψ. Точное решение уравнения получается для атома водорода или водородоподобных ионов, а для многоэлектронных систем используются различные приближения. Квадрат волновой функции ψ2 определяет вероятность обнаружения электрона на том или ином расстоянии от ядра атома.
Согласно принципу Гейзенберга невозможно одновременно определить положение частицы в пространстве и её импульс. Следовательно, нельзя рассчитать траекторию движения электрона в поле ядра, можно лишь оценить вероятность его нахождения в атоме с помощью волновой функции ψ, которая заменяет классическое понятие траектории. Волновая функция ψ характеризует амплитуду волны в зависимости от координат электрона, а ее квадрат ψ2 определяет вероятность нахождения электрона в определенной точке пространства.
В связи с новыми представлениями о движении электров в атомах в квантовой механике появляется новое понятие – атомная орбиталь.
Атомная орбиталь (АО) – область атомного пространства, в которой движется электрон. Форму АО характеризуют линиями и поверхностями с одинаковым значением ψ2, которую называют плотностью электронного облака.
Таким образом, атомной орбитали соответствует волновая функция ψ. Атомная орбиталь характеризуется энергией, формой и направлением в пространстве. Все эти характеристики квантованы (изменяются скачками), они описываются с помощью квантовых чисел.
Квантовые числа
Состояние электрона в атоме описывают четыре квантовых числа, которые характеризуют энергию электрона, форму электронного облака, его ориентацию в пространстве и его спин. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.
Главное квантовое число(n) характеризует энергию электрона на данном энергетическом уровне, определяет размеры атомной орбитали, используется как номер энергетического уровня Главное квантовое число имеет значения от 1 до ¥ (n = 1, 2, 3, 4... ¥). Иногда энергетические уровни обозначают буквами K, L, M, N.., которые соответствуют численным значениям 1, 2, 3, 4…. Чем меньше n, тем больше энергия взаимодействия электрона с ядром.
При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном. 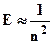
Орбитальное квантовое число (l) определяет форму атомной орбитали и принимает значения от 0 до (n-1), то есть n значений. Орбитальное квантовое число принято обозначать буквенными символами:
| l | = | |||||
| s | p | d | f | g |
Электроны с одинаковым значением l образуют в атоме энергетический подуровень.
Таблица 2.2
Обозначение орбитального квантового числа и подуровней
| n (энергетический уровень) | l (энергетический подуровень) | Обозначение подуровней |
| 1s | ||
| 0, 1 | 2s, 2p | |
| 0, 1, 2 | 3s, 3p, 3d | |
| 0, 1, 2, 3 | 4s, 4p, 4d, 4f |
Каждому значению l соответствует орбиталь определенной формы. Решение уравнения Шредингера показало, что s-орбиталь (l = 0) имеет форму шара, p-орбиталь (l =1) - форму гантели и т. д. (рис. 2.1).
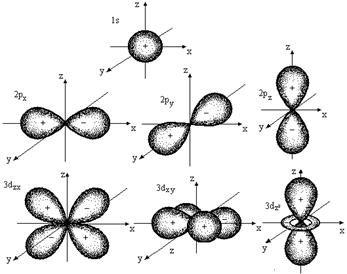
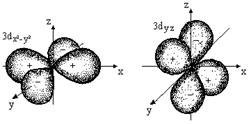
Рис. 2.1. Формы атомных орбиталей
Для электронов первого энергетического уровня (n = 1) возможна только одна форма орбитали (s), для второго (n = 2) - две (s и p) и т. д. Таким образом, энергетические уровни состоят из одного или нескольких энергетических подуровней. Для n = 1 возможен только один подуровень с l = 0, для n = 2 - два с l = 0 и l =1 и т д.
Состояние электрона в атоме обозначают цифрами и буквами. Например, электрон, у которого n = 1 и l = 0, обозначают 1s. Состояние 4p означает, что электрон находится на четвертом энергетическом уровне (n = 4); форма орбитали соответствует гантели (l = 1) и т.д.
Магнитное квантовое число (m) - характеризует пространственную ориентацию орбитали. Оно зависит от орбитального квантового числа и принимает значения от –l до нуля и от нуля до +l. Например, если орбитальное квантовое число равно 0 (s-орбиталь), то магнитное квантовое число имеет одно значение (0), если орбитальное квантовое число равно 1 (р-орбиталь), то магнитное квантовое число имеет три значения: –1, 0 и +1, а если орбитальное квантовое число равно 2 (d-орбиталь), то магнитное квантовое число имеет пять значений: –2, –1, 0, +1 и +2 и т.д. Таким образом, для каждого значения l имеется (2l + 1) значений m.
Все орбитали одного подуровня l обладают одинаковой энергией, но по-разному ориентированы относительно друг друга (рис 2.1).
Такие состояния электронов в квантовой механике называются вырожденными:р-состояние трехкратно вырождено, d-состояние - пятикратно и т.д. (табл. 2.3).
Таблица 2.3
Подуровни и атомные орбитали
| l (подуровень) | m (орбиталь) | Число АО с данным значением l | Графическое обозначение орбиталей |
 0 (s) 0 (s)
| (s) | ||
   1 (p) 1 (p)
| +1, 0, –1 | (p) | |
     2 (d) 2 (d)
| +2, +1, 0, –1, –2 | (d) | |
       3 (f) 3 (f)
| +3, +2, +1, 0, –1, –2, –3, | (f) |
Изучение атомных спектров показало, что трех квантовых чисел недостаточно для описания свойств электронов.

 Дополнительное четвертое квантовое число -спиновое(s) ("spin" - вращение, веретено) - характеризует собственный механический момент движения электрона, которое условно представляют как вращение вокруг собственной оси. Оно может происходить в двух взаимно противоположных направлениях. Поэтому спиновое квантовое число имеет только два значения: +1/2 и - 1/2. Наличие спина у электрона было подтверждено экспериментально. Электроны с разными спинами обозначаются стрелками, направленными вверх
Дополнительное четвертое квантовое число -спиновое(s) ("spin" - вращение, веретено) - характеризует собственный механический момент движения электрона, которое условно представляют как вращение вокруг собственной оси. Оно может происходить в двух взаимно противоположных направлениях. Поэтому спиновое квантовое число имеет только два значения: +1/2 и - 1/2. Наличие спина у электрона было подтверждено экспериментально. Электроны с разными спинами обозначаются стрелками, направленными вверх 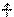 и вниз
и вниз 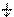 .
.
Дата добавления: 2016-07-05; просмотров: 5675;











