Скорость произвольной точки М плоской фигуры равняется скорости, которую она имеет в относительном вращении вокруг МЦС.
Следовательно:
1. скорость 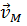 направлена перпендикулярно отрезку РМ в сторону вращения;
направлена перпендикулярно отрезку РМ в сторону вращения;
2. модуль ее в соответствии с формулой (3.3) равен
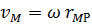 . (3.5)
. (3.5)
Картина распределения скоростей точек движущейся плоской фигуры имеет вид, показанный на рис. 3.7.
Рис. 3.7
3.4.Нахождение мгновенного центра скоростей
Рассмотрим несколько простых приемов, позволяющих в процессе решения задач определить местоположение МЦС.
1. Известна угловая скорость фигуры 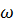 и скорость любой ее точки
и скорость любой ее точки  (рис. 3.8,а).
(рис. 3.8,а).
Для определения МЦС надо:
· Повернув вектор скорости 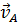 , на 900 в сторону вращения тела, найти направление, на котором лежит МЦС;
, на 900 в сторону вращения тела, найти направление, на котором лежит МЦС;
· На найденном направлении отложить отрезок AР равный 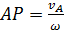 и получить положение точки Р, которая является мгновенным центром скоростей.
и получить положение точки Р, которая является мгновенным центром скоростей.
2. Известны направления скоростей двух точек плоской фигуры 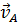 и
и 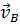 и эти скорости не параллельны друг другу (рис. 3.8, б).
и эти скорости не параллельны друг другу (рис. 3.8, б).
Для определения МЦС надо из точек А и В восстановить перпендикуляры к направлению скоростей до точки их пересечения P, которая и будет точкой МЦС.
При этом  .
.
Рис. 3.8
3. Cкорости двух точек плоской фигуры 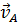 и
и 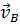 параллельны друг другу и перпендикулярны отрезку АВ.
параллельны друг другу и перпендикулярны отрезку АВ.
МЦС находится из условия, что модули скоростей точек А и В пропорциональны расстояниям от этих точек до МЦС:
 .
.
Возможны два варианта:
· МЦС находится между точками А и В, когда скорости направлены в разные стороны (рис.3.8, в);
· МЦС находится за пределами отрезка АВ, когда скорости не равны и направлены в одну сторону (рис. 3.8, г).
4. Cкорости двух точек плоской фигуры 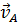 и
и 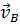 равны по модулю и параллельны друг другу. При этом они могут быть перпендикулярны или неперпендикулярны отрезку АВ.
равны по модулю и параллельны друг другу. При этом они могут быть перпендикулярны или неперпендикулярны отрезку АВ.
МЦС в этом случае располагается в бесконечности. Скорости всех точек тела одинаковы. Движение тела является мгновенно поступательным и 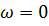 .
.
5. При качении тела по неподвижной поверхности (Рис. 3.9) скорости соприкасающихся точек равны в том случае, если отсутствует проскальзывание между телами. Тогда МЦС находится в точке соприкосновения тела с поверхностью.
Рис. 3.9
3.5.Теорема о сложении ускорений
ТЕОРЕМА
Ускорение точки плоской фигуры равно векторной сумме ускорения полюса и ускорения, которое имеет эта точка в относительном вращении фигуры вокруг полюса:
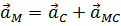 . (3.6)
. (3.6)
Доказательство
По теореме о сложении скоростей имеем:
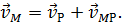
Продифференцируем это равенство по времени. Получим:
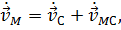
где 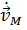 – ускорение точки М,
– ускорение точки М, 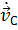 − ускорение точки С,
− ускорение точки С,
 ускорение точки М в системе отсчета, связанной с точкой С, то есть ее ускорение во вращении фигуры вокруг точки С (вокруг полюса).
ускорение точки М в системе отсчета, связанной с точкой С, то есть ее ускорение во вращении фигуры вокруг точки С (вокруг полюса).
Теорема доказана.
Рис. 3.10
Ускорение 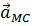 определяется по правилам вращательного движения, то есть равно сумме вращательного и центростремительного ускорений (рис. 3.10):
определяется по правилам вращательного движения, то есть равно сумме вращательного и центростремительного ускорений (рис. 3.10):
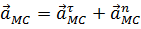 . (3.7)
. (3.7)
Тогда полное ускорение точки М будет равно:
 .
.
3.6. Скорости и ускорения точек колеса
ПРИМЕР
Пусть колесо радиусом R=1м катится без скольжения по горизонтальной плоскости. Скорость центра колеса 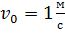 , а ускорение центра колеса по направлению совпадает со скоростью и равно
, а ускорение центра колеса по направлению совпадает со скоростью и равно 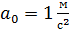 .
.
Определить скорости и ускорения точек А, В, С, Р, расположенных на ободе колеса (рис. 3.11).
Решение
Дата добавления: 2020-06-09; просмотров: 184;










