Приложения производной к исследованию функции

Определение 1.Функция 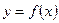называется возрастающей (убывающей) на множестве 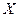, если для любых 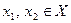из условия 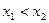следует условие 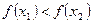( 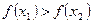), т.е. большему значению аргумента соответствует большее (меньшее) значение функции.

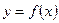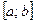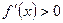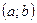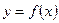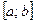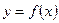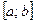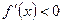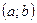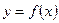Теорема 1.Если функция непрерывна на отрезке и её производная всюду на интервале , то строго возрастает на . Если функция непрерывна на отрезке и её производная всюду на интервале , то строго убывает на .

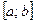Определение 2.Пусть функция 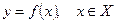, определена в некоторой окрестности точки 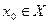и непрерывна в этой точке. Точка 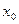называется точкой максимума (минимума) функции, если существует её окрестность, для всех точек которой выполняется неравенство 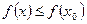( 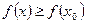), причём знак равенства имеет место лишь в случае .

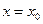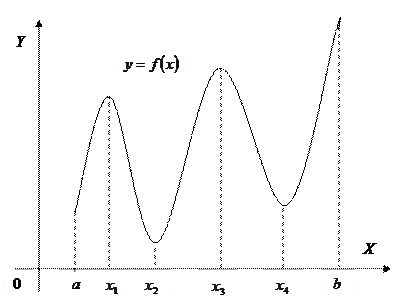Точки максимума и минимума называют точками экстремума.

Теорема 2 (необходимое условие существования экстремума). Если дифференцируемая функция 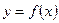имеет в точке 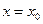максимум или минимум, то её производная обращается в нуль в этой точке, т.е.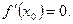

В точках, в которых производная не существует, может быть или максимум, или минимум, но может ни быть, ни того, ни другого.

Значения аргумента, при которых производная равна нулю или не существует, называются критическими точками.

Теорема 3(достаточное условие существования экстремума). Пусть функция 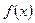непрерывна в некотором интервале, содержащем критическую точку 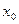, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки 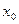). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при 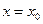функция имеет максимум. Если же при переходе через точку 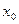слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

Пример 1. Исследуйте на экстремум функцию .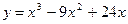

Решение. Имеем:

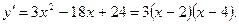
Приравняем производную к нулю и найдем критические точки: 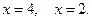При переходе через точку 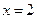производная меняет знак с «+» на «-», значит, в этой точке функция имеет максимум. При переходе через точку 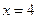производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. Результаты исследования сведены в таблицу:

x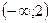
	+		-		+
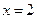
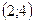
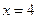
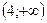
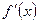
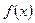
	возрастает		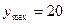убывает		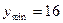возрастает

Ответ: .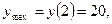

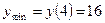Если функция 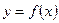непрерывна на отрезке 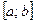, то на этом отрезке данная функция принимает и своё наибольшее, и своё наименьшее значения.

Для того чтобы найти наибольшее (наименьшее) значение функции 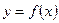на отрезке 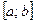, нужно:

1) найти производную данной функции;

2) найти критические точки;

3) вычислить значения функции в найденных точках и на концах отрезка;

4) из всех найденных значений выбрать наибольшее (наименьшее).

Пример 2. Найдите наибольшее и наименьшее значения функции 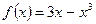на отрезке .

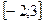Решение. Находим производную 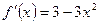и критические точки 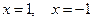. Определяем значения функции в критических точках и на концах отрезка:

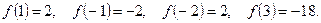
Из полученных значений выбираем наибольшее и наименьшее.

Итак, наибольшее значение функции на данном отрезке равно 2, а наименьшее -18.

Ответ: 2; -18.

Задачи.

1. Сумма целых значений 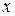, принадлежащих промежутку (или промежуткам) убывания функции 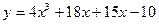равна

1) -2

2) 9

3) 7

4) -5

5) 11

6) -3

7) 8

8) 0

2. Длина интервала возрастания функции 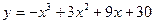равна

1) 1

2) 2

3) 3

4) 4

5) 7

6) 8

7) 10

8) 12

3. Точкой максимума функции 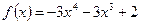является точка 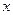, равная

1) 0

2) 1

3) -1

4) 0,5

5) -0,5

6) 0,75

7) -0,75

8) 2

4. Определите точку минимума функции .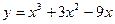

1) 2

2) 7

3) 11

4) 8

5) 9

6) 5

7) 1

8) 0

5. Найдите максимум функции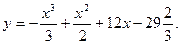

6. Найдите минимум функции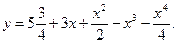

7. Сумма наибольшего и наименьшего значений функции 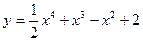на отрезке [-3;1] равна

1) 9,5

2) -5,5

3) 4,5

4) -9,5

5) 5,5

6) 3

7) 0

8) 4

8. Сумма наибольшего и наименьшего значений функции 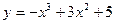на отрезке [1;3] равна

1) 9

2) 14

3) 5

4) 0

5) -5

6) -9

7) 3

8) 4

9. Наименьшее значение функции 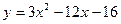на отрезке [-3;8] равно

1) -10

2) 10

3) -25

4) -28

5) 5

6) 1

7) -11

8) -26

9) -5

10) -27

11) -3

12) -1

10. Наибольшее значение функции 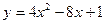на отрезке [0;3] равно

1) 1

2) 12

3) 13

4) 14

5) 15

6) 16

7) 3

8) 2