Принцип стереографического проектирования. Сетка Вульфа.

В кристаллографии для пространственного изобра­жения изучаемых кристаллов, их элементов симметрии и элементов ограничения используются различные про­екции. Наиболее часто применяются стереографическая (от греч. «стерсос» — пространственный, объемный) проекции.

Для построения проекции кристалла последний поме­щается в центр шаровой сферической поверхности. Гра­ни и ребра кристалла продолжаются до пересечения с шаровой поверхностью и изображаются так: грани — в виде дуг, ребра —в виде точек. Такая проекция получи­ла название стереографической. При построении стереографической проекции кри­сталла для его более полного отображения практикует­ся нанесение на проекцию элементов симметрии данного кристалла. Условились элементы симметрии изображать следующими значками

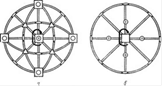
Сетка Вульфа в кристаллографии — стереограмма градусной сетки на сфере при точке зрения на экваторе сферы. Меридианы и параллели сетки Вульфа играют только вспомогательную роль как проекции дуг больших и малых кругов.

Все построения с использованием сетки Вульфа проводятся на кальке, на которой фиксируется центр, совпадающий с истинным полюсом (N) сферы проекций (φ=…, ρ=0), и точка пересечения нулевого меридиана с окружностью сетки Вульфа (φ=0, ρ=90). Погрешность сетки Вульфа составляет 2°.

Метод изобретён кристаллографом Георгием Вульфом.

Примеры примененияС помощью сетки Вульфа можно построить стереографическую проекцию точки, заданной своими сферическими координатами φ и ρ: углы φ отсчитывают по окружности сетки Вульфа по часовой стрелке от нулевого меридиана, а углы ρ — от центра сетки по горизонтальному или вертикальному диаметру, с концом которого, вращая кальку (не нарушая центровку), совмещают точку-зарубку, отвечающую координате φ.

Сетка Вульфа позволяет графически, без дополнительных расчётов решать многие задачи геометрической кристаллографии, связанные с угловыми характеристиками кристаллов.

11. Простые формы. Принцип вывода.Простая форма – совокупность граней, связанных между собой элементами симметрии. Это фигура, состоящая из симметричных граней, ее грани должны быть связаны хотя бы с одним элементом симметрии. L2 – ДИЭДР, ПИНАКОИД, МОНОЭДР. Аналогично относительно осей порядков выше находятся простые формы. При определении простых форм может помочь стереографическая проекция.

12. Закон Вейса (2 закон кристаллографии) стр. 154Любая грань кристалла принадлежит по меньшей мере двум его поясам. Или Плоскость параллельная двум ребрам кристалла, представляет собой возможную грань его, а прямая, параллельная линии пересечении дух граней кристалла, является его возможным ребром.

Согласно этому закону на пересечении двух поясов теоретически всегда возможна грань.

Пояс – это совокупность граней, пересекающихся по параллельным ребрам, а они располагаются параллельно атомным рядам.

13. Закон Гаюи (3 закон кристаллографии)Двойные отношения параметров, отсекаемых двумя другими гранями кристаллов на трех пересекающихся ребрах его, равны отношениям целых сравнительно малых чисел. Нужен для определения символов граней:

A’/a – b’/b – c’/c =h-k-l.

14. Символы граней кристаллов Символ грани Ах, Вх, Сх выражается тремя целыми и взаимно простыми числами, представляющими собой отношения трех дробей, числители которых являются параметрами единичной грани (ОА1, ОВ1, ОС1), а знаменатели соответствуют параметрам заданной грани (ОАх, ОВх, ОСх)

Для получения символов граней необходимо за координатные оси принять три направления, проходящие через одну точку и параллельные трем ребрам кристалла, а также выбрать единичную грань. (Берутся обратные величины от отношений) символ грани (hkl)

15. Скорость роста и ретикулярная плотность граней кристаллов. Скорость роста грани – величина нормали, на которую переместилась данная грань за единицу времени.

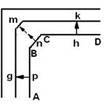AB, BC, CD – грани кристалла pg, mn, hk – скорости роста граней кристалла.

Анизотропия свойств кристаллов проявляется в разных скоростях роста. Например, грани с наибольшей ретикулярной плотностью (т.е. плотностью расположения частиц на плоской сетке решетки) растут с наименьшей скоростью. Поэтому грань ВС со временем исчезает, т.к. скорость ее роста меньше скорости роста граней AB и CD.

В соответствии с теорией роста, образование нового слоя начинается только после завершения формирования последующего. Так создается идеальный кристалл – выпуклый многогранник с плоскими гранями.

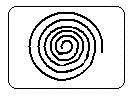Однако грани реальных кристаллов нередко отличаются наличием бугорков, впадин, штриховок – это так называемая скульптура грани. Более того, впервые на кристаллах корунда, а затем и на гематите, кварце, сфалерите были обнаружены на поверхности кристалла тончайшие спирали (рис. 2.3). Оказалось, что именно по этим винтовым лестницам, которые являются проявлением линейных дефектов кристаллических решеток (называемыми дислокациями), и растут кристаллы.