Логические элементы.
Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.
Логические функции отрицания, дизъюнкции (логическое сложение) и конъюнкции (логическое умножение) реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором (рис.1).
Из указанных простейших базовых логических элементов конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др.
Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч элементов.
Это возможно потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые операции).
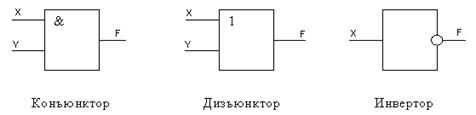
Рисунок 1 – Логические схемы
Принцип действия логических схем принято пояснять таблицами истинности, которые отражают функциональную зависимость выхода (Q) от входов (А, В, С и т.д.). Наличие сигнала отражается 1, его отсутствие 0.
1. Элемент НЕ (инвертор)
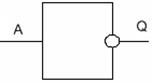
Рисунок 2 – Условное обозначение элемента "НЕ"
Электронный логический элемент НЕ имеет на выходе сигнал логической 1, если на входе 0 и логического 0, если на входе логическая 1. Работу схемы отражает таблица истинности:
| Вход | A | ||
| Выход | Q |
2. Элемент И (конъюнктор)

Рисунок 3 – Условное обозначение элемента "И" с двумя входами.
Электронный логический элемент И имеет на выходе сигнал логической 1, соответствующий значению "истина" только тогда, когда на все его входы (два или более) поданы сигналы логической единицы; в противном случае на выходе этого элемента будет логический 0, соответствующий значению "ложь". Работу схемы отражает таблица истинности:
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
3. Элемент ИЛИ (дизъюнктор).

Рисунок 4 – Условное обозначение элемента "ИЛИ" с двумя входами
Электронный логический элемент, на выходе которого логический 0 (значение "ложь") появляется только тогда, когда на все его выходы (два и более) поданы сигналы логического 0; во всех остальных случаях на выходе появляется логическая 1 (значение "истина"). Этот элемент реализует логическую операцию ИЛИ. Работу схемы отражает таблица истинности:
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
4. Элемент И-НЕ (штрих Шеффера).
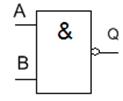
Рисунок 5 – Условное обозначение элемента "И-НЕ" с двумя входами
Электронная логическая схема, в которой выходной сигнал имеет уровень логической 0 (ложь) только тогда, когда на всех ее входах действуют сигналы логической 1. Во всех других случаях на его выходе появляется логическая 1. Работу схемы отражает таблица истинности:
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
5. Элемент ИЛИ-НЕ (стрелка Пирса).
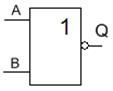
Рисунок 6 – Условное обозначение элемента "ИЛИ-НЕ" с двумя входами
Электронная логическая схема, на выходе у которой появляется логическая 1 только тогда, когда на все ее входы поданы сигналы логического 0, а в любых других случаях на выходе схемы действует уровень логического 0.
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
6. Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ
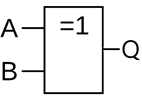
Рисунок 7 – Условное обозначение элемента "ИСКЛЮЧАЮЩЕЕ ИЛИ" с двумя входами
Электронный логический элемент, выходной сигнал которого равен 1 только в тех случаях, когда один из входных сигналов равен логической 1, а остальные - логическому 0. называется элементом отрицания эквивалентности. Его можно использовать, как простой цифровой компаратор, используется как контроль на четность. Элемент выполняет операцию сложения по модулю 2. для суммы по модулю 2 с любым количеством входов на выходе будет:
1- тогда и только тогда, когда на входе действует нечётное количество «1»,
0- тогда и только тогда, когда на входе действует чётное количество «1».
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
7. Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ
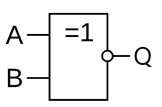
Рисунок 8 – Условное обозначение элемента "ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ" с двумя входами
Электронный логический элемент, выходной сигнал которого равен логическому 0 только в тех случаях, когда один из входных сигналов равен 1, а остальные - логическому 0. В противном случае выходной сигнал равен логической 1. Этот элемент реализует логическую операцию эквивалентности, т.е. на выходе будет:
1 - тогда и только тогда, когда на входе действует чётное количество «1» или «0».
0 - тогда и только тогда, когда на входе действует нечётное количество «1».
| Вход 1 | A | ||||
| Вход 2 | В | ||||
| Выход | Q |
Сигнал, выработанный одним логическим элементом, можно подавать на вход другого логического элемента. Это дает возможность образовывать цепочки из отдельных логических элементов. Цепочку из логических элементов будем называть логическим устройством. Схемы, соответствующие таким устройствам, называют функциональными.
На рис. 9 показан пример такой цепочки.
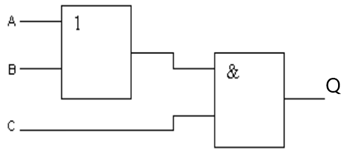
Рисунок 9 – Логическое устройство, собранное на элементах ИЛИ и И
В этом устройстве выполняется операция логического сложения А и В, А затем логическое умножение результата на С. Таблица истинности будет иметь вид:
| А | В | С | Q |
При составлении таблицы истинности, столбцы А, В, С заполняются стандартно: первая строчка соответствует двоичному коду десятичного числа 0, вторая строчка - двоичному коду десятичной 1, третья – двоичный код числа 2, четвертая – двоичный код числа 3 и т.д. Значения выхода находят как результат логических операций.
Дата добавления: 2020-06-09; просмотров: 1033;











