МЕТОД АНГЕРА-ПОЛА МИНИМИЗАЦИИ ТАБЛИЦ ПЕРЕХОДОВ АСИНХРОННЫХ КОНЕЧНЫХ АВТОМАТОВ
В процессе минимизации необходимо найти совместимые состояния автомата, то есть такие состояния, которые покрываются одной и той же строкой минимизированной таблицы переходов. Очевидно, что необходимым условием совместимости двух состояний АП (строк таблицы переходов) является совместимость выходных сигналов в тех столбцах, где они определены (совместимость по выходам).
Поиск совместимых строк удобно производить с помощью специальной треугольной таблицы, в которой отмечаются условия совместимости и эквивалентности строк. Рассмотрим построение такой таблицы на примере автомата, заданного табл. 10.
Таблица 10
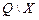
| ||||
| (0),0 | * | |||
| * | * | (1),1 | ||
| (2),0 | * | |||
| * | (3),1 | |||
| (4),1 | * | |||
| * | (5),0 | |||
| * | (6),0 | |||
| (7),1 |
Строки треугольной таблицы совместимости (таблицы Ангера-Пола, табл. 11) обозначаются состояниями автомата кроме нулевого, а столбцы состояниями кроме последнего. В клетки указанной таблицы вносятся следующие обозначения:
 – состояния неэквивалентны (несовместимы).
– состояния неэквивалентны (несовместимы).
 – состояния безусловно совместимы.
– состояния безусловно совместимы.
 – строки совместимы при условии совместимости указанных строк (
– строки совместимы при условии совместимости указанных строк ( 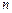 и
и  ).
).
Таблица 11

После заполнения таблицы вычёркиваем те клетки, для которых условие совместимости пар не выполняется (пунктирные линии в табл. 11). Например, строки 0 и 4 несовместимы, следовательно, не будут совместимы и строки (2, 4), (4, 7), (6, 7) и т. д.
Из таблицы Ангера-Пола можно выписать достаточно большое количество групп совместимых строк. Задача сводится к определению минимального количества групп, необходимого для покрытия исходной таблицы переходов. Это удобно делать с помощью таблицы покрытий Квайна-Мак-Класски (табл. 12). По столбцам располагаем исходные состояния автомата, по строкам – максимально – совместимые группы состояний (строк).
На пересечении строк и столбцов точками отмечаем те состояния, которые входят в максимально совместимые группы. Далее кружком отмечаем те состояния, которые покрываются всего один раз (то есть одна точка в столбце). Остальные состояния необходимо покрыть минимальным количеством групп.
Таблица 12

Кодируем новые состояния автомата (табл. 13).
Таблица 13
| Группа (строка) | Код |
| (0, 1) | |
| (1, 3) | |
| (2, 7) | |
| (4,5,6) |
Далее строим минимизированную таблицу переходов (табл. 14).
Таблица 14
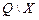
| ||||
| (0),0 | ||||
| * | (1),1 | |||
| (2),0 | (2),1 | |||
| (3),1 | (3),0 | (3),0 |
В общем случае, при большом числе входных сигналов и не полностью заполненных таблицах переходов (то есть используются не все комбинации входных переменных), возможна минимизация количества столбцов. При этом на входе автомата выделяется комбинационная схема, осуществляющая перекодирование входных сигналов в управляющие сигналы автомата. Для осуществления такой операции количество различных столбцов должно быть как минимум в два раза меньше общего количества столбцов таблицы переходов.
Рассмотрим ещё один пример минимизации таблицы переходов КА, заданного табл. 15.
Таблица 15
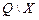
| ||||
| (0),0 | ||||
| (1),0 | ||||
| (2),1 | ||||
| (3),0 | ||||
| (4),0 | ||||
| (5),0 | ||||
| (6),0 | ||||
| (7),1 |
Строим таблицу Ангера-Пола (табл. 16).
Таблица 16
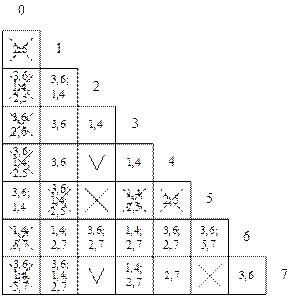
Кодируем группы совместимых строк (табл. 17)
Таблица 17
| Группа (строка) | Код |
| (0, 5) | |
| (1, 2, 3, 4, 5, 6, 7) |
Минимизированная таблица переходов (табл. 18).
Таблица 18
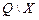
| ||||
| (0),0 | (0),0 | |||
| (1),0 | (1),0 | (1),1 |
Дата добавления: 2020-06-09; просмотров: 1094;











