Токи и потокосцепления синхронной машины в начальный момент внезапного нарушения режима.
Физическую картину переходного процесса в синхронной машине рассмотрим при некоторых упрощающих допущениях. Будем считать КЗ симметричным, тогда процессы во всех трех фазах протекают практически одинаково и достаточно рассмотреть любую из фаз. Кроме того, примем магнитную цепь машины ненасыщенной, что позволяет применить принцип наложения магнитных потоков.
Рассмотрим картину магнитного поля генератора при КЗ (рис.7.2).
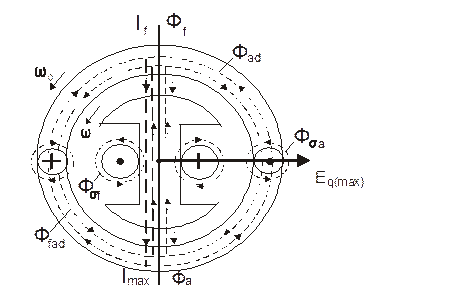
Рис.7.2.
Ток if обмотки возбуждения определяет собственное потокосцепление Ψf этой обмотки:
if ═>Ψf,
которое может быть представлено в виде суммы
Ψf = Ψfad + Ψσf,
где Ψfad – часть потокосцепления обмотки возбуждения, которая
обусловлена магнитным потоком Фfad, сцепленным также с обмоткой
статора;
Ψσf – потокосцепление рассеяния обмотки возбуждения, обусловленное
потоком рассеяния Фσf сцепленным только с обмоткой возбуждения.
При коротком замыкании сопротивление обмотки статора является практически только индуктивным, поэтому ток статора ia отстает от ЭДС статора Еq на угол φК ≈ 900. Максимум ЭДС наводится в проводнике статорной обмотки находящемся на продольной оси ротора, тогда максимальный ток статора, в соответствии со сказанным выше, будет в проводнике находящимся на поперечной оси ротора справа от вертикали (рис.7.2). Ток статора создает магнитный поток Фa сцепленный одновременно с обмотками статора и ротора Фаd и магнитный поток Фσа рассеяния статора, сцепленный только с обмоткой статора. Потокосцепление обмотки статора можно представить соответственно
Ψа = Ψad + Ψσa
Ток возбуждения if и ток статора ia в синхронной машине действуют одновременно, поэтому полное потокосцепление обмотки возбуждения с учетом влияния тока статора
ΨfΣ = Lfif + Mfaia , . (7.1)
где Lf – индуктивность обмотки возбуждения генератора;
Mfa – взаимная индуктивность обмотки возбуждения и обмотки
статора.
Дифференциальное уравнение для цепи возбуждения, не содержащей посторонних ЭДС:
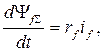 (7.2)
(7.2)
где rf – активное сопротивление цепи возбуждения.
Если принять, что цепь возбуждения является сверхпроводящим контуром (rf = 0), то из выражения (7.2) получим
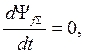 (7.3)
(7.3)
тогда ΨfΣ = const. С учетом малого активного сопротивления rf обмотки возбуждения ее можно считать сверхпроводящим контуром и применить к ней принцип постоянства потокосцепления сверхпроводящего контура. С учетом этого допущения продифференцируем (7.1) и получим:
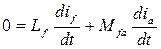 , (7.4)
, (7.4)
или в конечных приращениях
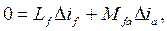
отсюда
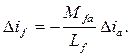 (7.5)
(7.5)
Умножив числитель и знаменатель (7.5) на ω, найдем:
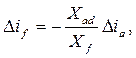 (7.6)
(7.6)
где Хad = Mfaω –сопротивление взаимоиндукции обмотки статора по
продольной оси;
Хf = Lfω = Xad + Xσf – полное индуктивное сопротивление цепи
возбуждения.
Формула (7.6) является математическим выражением закона Ленца в применении к синхронной машине. Данное выражение показывает, что в начальный момент ВНР приращение тока статора 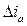 вызовет реакцию обмотки возбуждения – приращение тока возбуждения машины
вызовет реакцию обмотки возбуждения – приращение тока возбуждения машины 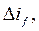 причем приращение потокосцепления статора
причем приращение потокосцепления статора 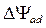 от тока
от тока 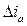 и приращение потокосцепления
и приращение потокосцепления 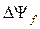 от тока
от тока 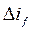 компенсируют друг друга, т.е.
компенсируют друг друга, т.е.
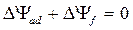 (7.7)
(7.7)
или
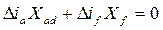
Дата добавления: 2020-05-20; просмотров: 630;











