Кинематика рабочей среды в радиальных турбинных ступенях
Рассмотрим процесс преобразования энергии в радиальной турбинной ступени. Для конкретности будем рассматривать центростремительную ступень, хотя все выводы и расчетные формулы справедливы и для центробежной ступени.
Принципиальная конструктивная схема такой ступени показана на рис. 64. Пар подводится к неподвижному сопловому аппарату, закрепленному на корпусе турбины, и затем поступает на рабочие лопатки, закрепленные на диске параллельно оси турбины. На рис. 65 показано сечение ступени плоскостью, нормальной оси турбины, и треугольники скоростей.
 В отличие от осевой ступени, где в качестве одного из основных размеров рассматривается средний диаметр ступени, в радиальной ступени следует различать:
В отличие от осевой ступени, где в качестве одного из основных размеров рассматривается средний диаметр ступени, в радиальной ступени следует различать:
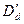 -диаметр входных кромок сопел (направляющих лопаток);
-диаметр входных кромок сопел (направляющих лопаток);
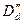 - диаметр выходных кромок сопел (направляющих лопаток);
- диаметр выходных кромок сопел (направляющих лопаток);
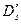 - диаметр входных кромок рабочих лопаток;
- диаметр входных кромок рабочих лопаток;
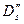 - диаметр выходных кромок рабочих лопаток.
- диаметр выходных кромок рабочих лопаток.
Прочие основные геометрические размеры радиальной и осевой ступеней соответствуют друг другу:
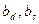 - хорда профиля направляющей и рабочей решеток;
- хорда профиля направляющей и рабочей решеток;
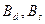 - ширина направляющей и рабочей решеток;
- ширина направляющей и рабочей решеток;
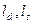 - высота сопел и рабочих лопаток;
- высота сопел и рабочих лопаток;
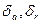 - осевой и радиальные зазоры.
- осевой и радиальные зазоры.
Для определения 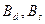 могут быть записаны очевидные равенства:
могут быть записаны очевидные равенства:
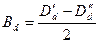 (2.9.1)
(2.9.1)
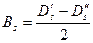 (2.9.2)
(2.9.2)
При необходимости различают высоту входных ( 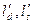 ) и выходных (
) и выходных ( 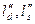 ) кромок каждой решетки.
) кромок каждой решетки.
В качестве среднего диаметра направляющего и рабочего венцов будем рассматривать диаметр окружности, проведенной через середину ширины венца
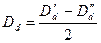 (2.9.3)
(2.9.3)
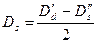 (2.9.4)
(2.9.4)
Развертывая окружность 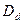 и
и 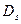 на плоскость (т.е. принимая
на плоскость (т.е. принимая 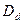 и
и 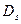
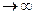 ), переходим к обычной схеме элементарной турбинной ступени (§ 2.1). Из этой схемы определяем:
), переходим к обычной схеме элементарной турбинной ступени (§ 2.1). Из этой схемы определяем:
Шаг решетки t, угол установки профилей 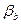 , а также углы потока, определяющие форму треугольников скоростей (§ 2.1).
, а также углы потока, определяющие форму треугольников скоростей (§ 2.1).
Построение процесса в диаграмме h-s для радиальной ступени ничем не отличается от подобного построения для осевой ступени (рис.15, 16, 17).
Расход пара, теоретические и действительные скорости потока, коэффициенты скорости и потерь кинетической энергии, степень реакции и другие характеристики полностью идентичны соответствующим понятиям для осевой ступени.
Расход пара, теоретические и действительные скорости потока, коэффициенты скорости и потерь кинетической энергии, степень реакции и другие характеристики полностью идентичны соответствующим понятиям для осевой ступени.
Существенное различие между радиальной и осевой ступенями начинает проявляться при рассмотрении процесса течения пара через каналы рабочих лопаток.
В обоих случаях анализ движения пара в рабочих лопатках связан с переходом к относительному движению пара , т.е. к вращающейся системе координат.
В общем случае уравнение энергии для этой системы координат, при условии, что потери энергии отсутствуют, может быть записано в виде:
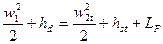 (2.9.5)
(2.9.5)
где: 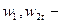 скорости пара на входе и на выходе из решетки.
скорости пара на входе и на выходе из решетки.
Индекс t при скорости w показывает, что рассматривается теоретический процесс, без учета потерь энергии;
hd, hst – энтальпии пара на входе в решетку и выходе из нее, в конце адиабаты расширения.
Очевидно, что
has = hd + hst (2.9.6)
LF – работа сил, появившихся в результате вращения новой системы координат, жестко соединенной с рабочими лопатками, с угловой скоростью ω при перемещении единицы массы рабочего вещества из входного сечения рабочей решетки в сечение.
Силы, определяющие работу LF, являются центробежной и кориолисовой силой. Однако кориолисова сила направлена нормально относительной скорости пара wи потому работа кориолисовой силы в относительном движении всегда равна нулю. В абсолютном движении пара кориолисовы силы совершают полезную работу, в частном случае когда w1 и w2 направлены по радиусу, вся полезная работа центростремительной ступени равна работе кориолисовых сил.
Центробежная сила направлена по радиусу. Поэтому в осевой ступени эта работа также равна нулю, а в радиальной ступени она определится произведением центробежной силы на перемещение элемента потока от сечения с радиусом r1 =D’s/2 к сечению радиусом r1 =Ds”/2 Если отнести эту работу к единице массы рабочего вещества, получим
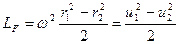 (2.9.7)
(2.9.7)
Таким образом, для радиальной ступени уравнение энергии (2.9.5) может быть переписано
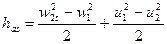 (2.9.8)
(2.9.8)
Непосредственно из ((2.9.8) может быть получено выражение для определения теоретической скорости истечения пара из каналов рабочей решетки радиальной ступени
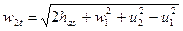 (2.9.9)
(2.9.9)
Дата добавления: 2016-06-29; просмотров: 2013;











