Последовательный ЦАП на переключаемых конденсаторах.

Рас­­­­смотренная выше схема ЦАП с ШИМ вначале преобразует цифровой код во временной интервал, который формируется с помощью двоичного счетчика квант за квантом, поэтому для получения n-разрядного преобразования необходимы 2ⁿ временных квантов (тактов). Схема последовательного ЦАП, приведенная на рис.13.3, позволяет выполнить цифро-аналоговое преобразование за значительно меньшее число тактов.

Рис.13.3. Схема последовательного ЦАП на

переключаемых конденсаторах

В этой схеме емкости конденсаторов С₁ и С₂ равны. Перед началом цикла преобразования конденсатор С₂ разряжается ключом S₄. Входное двоичное слово задается в виде последовательного кода. Его преобразование осуществляется последовательно, начиная с младшего разряда а₀. Каждый такт преобразования состоит из двух полутактов. В первом полутакте конденсатор С₁ заряжается до опорного напряжения U_оп при а₀=1 посредством замыкания ключа S₁ или разряжается до нуля при а₀=0 путем замыкания ключа S₂. Во втором полутакте при разомкнутых ключах S₁, S₂ и S₄ замыкается ключ S₃, что вызывает деление заряда пополам между С₁ и С₂. В результате получаем U₁(0)=U_вых(0)=(а₀/2)U_оп .

Пока на конденсаторе С₂ сохраняется заряд, процедура заряда конденсатора С₁ должна быть повторена для следующего разряда а₁ входного слова. После нового цикла перезарядки напряжение на конденсаторах будет

.

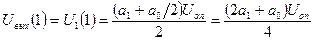Точно также выполняется преобразование для остальных разрядов слова. В результате для n-разрядного ЦАП выходное напряжение будет равно

.

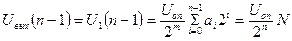Если требуется сохранять результат преобразования сколь-нибудь продолжительное время, к выходу схемы следует подключить устройство выборки и хранения УВХ. После окончания цикла преобразования следует провести цикл выборки, перевести УВХ в режим хранения и вновь начать преобразование.

Таким образом, представленная схема выполняет преобразование входного кода за 2n квантов, что значительно мень­ше, чем у ЦАП с ШИМ. Здесь требуется только два согласованных конденсатора небольшой емкости. Конфигурация аналоговой части схемы не зависит от разрядности преобразуемого кода. Однако по быстродействию последовательный ЦАП значительно уступает параллельным цифро-аналоговым преобразователям, что ограничивает область его применения.

ПАРАЛЛЕЛЬНЫЕ ЦАП

ЦАП с суммированием весовых токов.Большинство схем па­рал­лельных ЦАП основано на суммировании токов, сила каждого из которых пропорциональна весу цифрового двоичного разряда, при­чем должны суммироваться только токи разрядов, значения цифры в которых равны 1. Пусть, например, требуется преобразовать двоич­ный четы­рехразрядный код в аналоговый сигнал тока. У четвертого, старшего значащего разряда (СЗР) вес будет равен 2³=8, у третьего разряда - 2²=4, у второго - 2¹=2 и у младшего (МЗР) - 2⁰=1. Если вес МЗР I_МЗР=1 мА, то I_СЗР=8 мА, а максимальный выходной ток преоб­разователя I_{вых.макс}=15 мА и соответствует коду 1111₂. Понятно, что коду 1001₂, например, будет соответствовать I_вых=9 мА и т.д. Следо­вательно, тре­буется построить схему, обеспечивающую генерацию и коммутацию по заданным законам точных весовых токов. Простей­шая схема, реа­лизующая указанный принцип, приведена на рис.13.4.

.

Рис.13.4. Простейшая схема ЦАП с суммированием

весовых токов

Сопротивления резисторов выбирают так, чтобы при замкнутых ключах через них протекал ток, соответствующий весу разряда. Ключ должен быть замкнут тогда, когда соответствующий ему бит входного слова равен единице. Выходной ток определяется соотношением

.

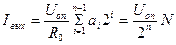При высокой разрядности ЦАП токозадающие резисторы должны быть согласованы с высокой точностью. Наиболее жесткие требо­ва­ния по точности предъявляются к резисторам старших разрядов, поскольку разброс токов в них не должен превышать тока младшего разряда. Поэтому разброс сопротивления в i-м разряде должен быть меньше, чем

ΔR / R=2^-i.

Из этого условия следует, что разброс сопротивления резистора, например, в четвертом разряде не должен превышать 3%, а в 10-м разряде - 0,05% и т.д.

Суммирование весовых токов наиболее целесообразно выполнить с помощью операционного усилителя по рис.13.5. Здесь представлена ба­зо­вая структурная схема 4-разрядного ЦАП (так называемая схема на взвешенных резисторах). Четыре би­та, фиксируемые в регистре, управляют состоянием четы­рёх ключей и обеспечивают 16 различных комбинаций. ОУ включён по схеме сумма­­­­­­­­­­тора. При замыкании одного из ключей выходное напряжение ЦАП определя­ется произведением опор­но­го напряжения U_оп на от­но­ше­ние сопротивлений резис­тора об­ратной связи ОУ к резистору матри­цы, находя­ще­му­ся в цепи данного ключа.

Рис.13.5. Базовая структурная

схема четырёхразрядного ЦАП

Если, например, замкнут ключ, соответствующий старшему зна­чащему разряду СЗР регис­тра (при установке в триггере этого разряда логической 1), то выходное напряже­ние U_вых= – (R/2R)U_оп = –U_оп / 2. При ус­­тановке уровня сигнала 1 в разряде 1 по­лу­чим U_вых = –(R/8R) U_оп= –U_оп/8. Замыкание каждого следующего ключа (в направле­нии уве­ли­че­ния веса разрядов) вы­зывает прирост выходного напря­же­ния, вдвое превышаю­щий результат замыкания пре­дыдущего клю­ча. При замы­ка­нии нескольких ключей резуль­тирующее выход­ное напряжение опреде­ляется суммой вкладов от каж­дого замкнутого клю­ча. Например, при ус­­тановке логической 1 в разрядах 3 и 1 полу­ча­ем выходное нап­ря­жение U_вых= –(U_оп / 2 + U_оп / 8). Таким обра­зом, можно получить 16 раз­личных дискретных уров­ней выходного нап­ряжения, соответствующих 16 различным двоич­ным комбинациям на входе ЦАП. Соотношения сопротивлений ре­зис­­торов должны быть вы­держаны с высокой точ­ностью для обеспе­чения необходимой ли­нейности преобразования вход­ного кода в вы­ходное напряжение.

Конструирование такого ЦАП на одном кристалле вызывает определённые трудности. Это объясняется слишком большим диапа­зо­ном величин сопротивлений вхо­дящих в него резисторов. В рас­смат­риваемом 4-разрядном ЦАП сопротивление резистора в цепи младшего значащего разряда МЗР должно быть в 16 раз больше сопротивления ре­зис­тора обратной связи. В об­щем случае для n–разрядного преобразователя нужны n+1 резистор, а сопро­тив­ление ре­зис­тора в цепи МЗР должно быть в 2ⁿ раз больше соп­ро­тивления резистора обратной связи. Реальное значение R, которое можно получить для резистора в рамках интегральной микросхемы, составляет 5-10 КОм. А в 8-разрядном ЦАП требуется 9 резисторов с сопротивлением от 5 КОм до 1.28 МОм (256 × 5 кОм), в то время как в 12-разрядном – 13 резисторов с нереальным диапазоном сопро­тивлений вплоть до 20.48 МОм.

Рассмотренная схема при всей ее простоте обладает целым букетом недостатков. Во-первых, при различных входных кодах ток, потребляемый от источника опорного напряжения (ИОН), будет различным, а это повлияет на величину выходного напряжения ИОН. Во-вторых, значения сопротивлений весовых резисторов могут различаться в тысячи раз, а это делает весьма затруднительной реализацию этих резисторов в полупроводниковых ИМС с необходимым классом точности. Кроме того, сопротивление резисторов старших разрядов в многоразрядных ЦАП могут быть соизмеримы с сопротивлением замкнутого ключа, а это приведет к погрешности преобразования. В-третьих, в этой схеме к разомкнутым ключам прикладывается значительное напряжение, что усложняет их построение.

Эти недостатки устранены в схеме ЦАП AD7520 (отечественный аналог 572ПА1), разработанном фирмой Analog Devices в 1973 г., которая в настоящее время является по существу промышленным стан­дартом (по ней выполнены многие серийные модели ЦАП). Указанная схема представлена на рис.13.6. В качестве ключей здесь исполь­-

Рис.13.6. Схема ЦАП с переклю­ча­телями и матрицей R-2R посто­-­

ян­ного импеданса

­зу­ют­ся МОП-тран­зисто­ры.

В этой схеме задание весовых коэффициентов ступеней преоб­разователя осуществляют посредством последовательного деления опорного напряжения с помощью резистивной матрицы R-2R посто­ян­ного импеданса. Основной элемент такой матрицы представляет собой делитель напряжения (рис.13.7), который должен удов­лет­во­рять сле­дую­щему условию: если он нагружен на сопротивление R_н, то его входное сопротивление R_вх также должно принимать значение R_н. Коэффициент ослабления цепи a=U₂/U₁ при этой нагрузке должен иметь заданное значение. При выполнении этих условий получаем следующие выражения для сопротивлений:

Рис.13.7. Построение ступени матрицы по­-

стоянного импеданса

.

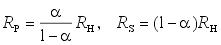При двоичном кодировании a =0,5. Если положить R_н=2R, то R_s=R и R_p=2R в соответствии с рис.13.6.

Поскольку в любом положении переключателей S_i они соединяют нижние выводы резисторов с общей шиной схемы, источник опорного напряжения нагружен на постоянное входное сопротивление R_вх=R. Это гарантирует неизменность опорного напряжения при любом входном коде ЦАП.

Согласно рис.13.6, выходные токи схемы определяются соотношениями

; ,

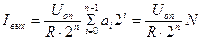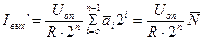а входной ток

.

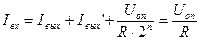Поскольку нижние выводы резисторов 2R матрицы при любом состоянии переключателей S_i соединены с общей шиной схемы через низкое сопротивление замкнутых ключей, напряжения на ключах всегда небольшие, в пределах нескольких милливольт. Это упрощает построение ключей и схем управления ими и позволяет использовать опорное напряжение из широкого диапазона, в том числе и различной полярности. Поскольку выходной ток ЦАП зависит от U_оп линейно, преобразователи такого типа можно использовать для умножения аналогового сигнала (подавая его на вход опорного напряжения) на цифровой код. Такие ЦАП называют перемножающими (MDAC).

На рис.13.8 показана схема ЦАП на резистивной матрице R-2R cо сложением весовых значений токов операционным усилителем.

Рис.13.8. ЦАП на сетке R-2R

Для доказательства возможности ис­пользования такой резистор­ной матрицы в схеме ЦАП рассмотрим величины токов в параллельных ветвях к суммирующей точке ОУ.

Потенциалы средней точки переключателей S₀,…S₃ вне зависи­мости от положения подвижного элемента (верхнее или нижнее) остаются одинаковыми и равными потенциалу земли, так как в нижнем положении они подключаются к клемме “земля”, а в верхнем поло­жении они подключаются к суммирующей точке операционного усили­теля ОУ, потенциал которой по условиям работы ОУ близок к потенциалу земли. Отсюда следует, что переключения S_i не вызывают изменения картины токов в резисторной матрице R-2R.

Рассмотрим картину токов в нижнем плече матрицы – точка a₀. К ней подключены два резистора с одинаковым номиналом 2R, то есть токи I₀ и I₀’ равны. Общее же сопротивление этих двух параллельно включенных резисторов R_0об = (2R*2R)/(2R+2R) = R.

По закону Кирхгофа ток I₁ = I₀ + I₀’ = 2I₀’. Сопротивление вертикального участка цепи между точкой а₁ и землёй равняется R₁ = R + R_0об = R + R = 2R, то есть равно сопротивлению горизонтального участка от этой же точки. Следовательно, протекающие по ним токи также равны: I₁ = I₁’. Так как I₁ = 2I₀’, то и I₁’ = 2I₀’. Общее же сопротив­ление резисторов, подключенных к точке а₁, по отношению к земле R_1об = (R₁*2R)/(R₁+2R) = (2R*2R)/(2R+2R) = R.

Рассуждая аналогично по отношению к точкам а₂, а₃, придём к соотношениям: I₂’ = 2I₁’ = 4I₀’, I₃’ = 2I₂’ = 8I₀’. Отсюда следует, что отно­ше­ния вели­чи­н токов в соседних параллельных ветвях матрицы кратны двум; их соотношения соответствуют коэффициентам 8-4-2-1, как это имеет место в схеме, показанной на рис.13.5. Поэтому схема на рис.13.8 реализует преобразование цифры в аналог по двоичной системе счисления.

Точность этой схемы снижает то обстоятельство, что для ЦАП, имеющих высокую разрядность, необходимо согласовывать сопро­тив­ления R₀ ключей на полевых транзисторах с разрядными токами. Особенно это важно для ключей старших разрядов. Например, в 10-разрядном ЦАП AD7520 ключевые МОП-транзисторы шести старших разрядов сделаны раз­ны­ми по площади и их сопротивление R₀ нарастает согласно двоич­ному коду (20, 40, 80, … , 640 Ом). Таким способом уравниваются (до 10 мВ) падения напряжения на ключах первых шести разрядов, что обеспечивает монотонность и линейность переходной характе­ристики ЦАП. 12-разрядный ЦАП 572ПА2 имеет дифференциальную нелинейность до 0,025% (1 МЗР).

ЦАП на МОП ключах имеют относительно низкое быстро­дей­ствие из-за большой входной емкости МОП-ключей. Тот же 572ПА2 имеет время установления выходного тока при смене вход­ного кода от 000...0 до 111...1, равное 15 мкс. 12-разрядный DAC7611 фирмы Burr-Braun имеет время установления выходного напряжения 10 мкс. В то же время ЦАП на МОП-ключах имеют минимальную мощность потребления. Тот же DAC7611 потребляет всего 2,5 мВт. В последнее время появились модели ЦАП рассмотренного выше типа с более высоким быстродействием. Так 12-разрядный AD7943 имеет время установления тока 0,6 мкс и потребляемую мощность всего 25 мкВт. Малое собственное потребление позволяет запитывать такие микромощные ЦАП прямо от источника опорного напряжения. При этом они могут даже не иметь вывода для подключения ИОН, например, AD5321.

ЦАП на источниках токаобладают более высокой точностью. В от­личие от предыдущего варианта, в котором весовые токи форми­ру­ются резисторами сравнительно небольшого сопротивления и, как следствие, зависят от сопротивления ключей и нагрузки, в данном слу­­­­чае весовые токи обеспечиваются транзистор­ными источниками то­ка, имеющими высокое динамическое сопро­тив­ление. Упрощенная схема ЦАП на источни­ках тока приведена на рис.13.9.

Рис.13.9. Схема ЦАП на

источ­никах тока

Весовые токи фор­ми­ру­ются с помощью резистивной матрицы. Потенциалы баз тран­зисторов одинаковы, а чтобы были равны и потенциалы эмиттеров всех транзисторов, площади их эмиттеров делают различными в соответствии с весовыми коэффициентами. Правый резистор матрицы подключен не к общей шине, как на схеме рис.13.4, а к двум параллельно включенным одинаковым транзисторам VT₀ и VT_н, в результате чего ток через VT₀ равен половине тока через VT₁. Входное напряжение для резистивной матрицы создается с помощью опорного транзис­тора VT_оп и операционного усилителя ОУ₁, выходное напряжение которого устанавливается таким, что коллекторный ток транзистора VT_оп принимает значение I_оп. Выход­ной ток для n-разрядного ЦАП

.

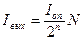Характерными примерами ЦАП на переключателях тока с биполярными транзисторами в качестве ключей являются 12-разрядный 594ПА1 с временем установления 3,5 мкс и погрешностью линейности не более 0,012% и 12-разрядный AD565, имеющий время установления 0,2 мкс при такой же погрешности линейности. Еще более высоким быстродействием обладает AD668, имеющий время установления 90 нс и ту же погрешность линейности. Из новых раз­работок можно отметить 14-разрядный AD9764 со временем уста­новления 35 нс и погрешностью линейности не более 0,01%. В качестве переключателей тока S_i часто используются биполярные дифференциальные каскады, в которых транзисторы работают в активном

Рис.13.10. Переключатель тока на дифференциаль-­

ных усилителях

режиме. Это позволя­ет сократить время ус­та­­­новления до еди­ниц на­носекунд. Схема переключателя тока на диффе­рен­циа­ль­ных усилителях приведена на рис.13.10.

Дифференциальные каскады VT₁-VT₃ и VT'₁-VT'₃ образованы из стандартных ЭСЛ вентилей. Ток I_к, протекающий через вывод кол­лектора выходного эмиттерного повторителя, является выходным током ячейки. Если на цифровой вход D_i подается напряжение высо­кого уровня, то транзистор VT₃ открывается, а транзистор VT'₃ закры­вается. Выходной ток определяется выражением

.

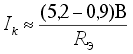Точность значительно повышается, если резистор R_э заменить источником постоянного тока, как в схеме на рис.13.9. Благодаря симметрии схемы существует возможность формирования двух выходных токов – прямого и инверсного. Наиболее быстро­действующие модели подобных ЦАП имеют входные ЭСЛ-уровни. Примером может служить 12-ти разрядный МАХ555, имеющий время установления 4 нс до уровня 0,1%. Поскольку выходные сиг­налы таких ЦАП захватывают радиочастотный диапазон, они имеют выходное сопротивление 50 или 75 Ом, которое должно быть согласовано с волновым сопротивлением кабеля, подключаемого к выходу преобразователя.

Принципы построения ЦАП для троичной системы счисле­ния.Познавательный интерес представляет возможность выполнения цифро-аналоговых преобразований для систем счисления с любым основанием. В общем случае ЦАП находит аналоговый эквивалент заданной кодовой комбинации последовательным выполнением операций сложения произведений веса каждого разряда на соответствующую цифру в этом разряде. Отсюда основой построения ЦАП является сумматор на операционном усилителе. Для типовой схемы ЦАП на взвешенных резисторах по рис.13.5 эквивалентом веса разряда является величина тока, протекающая через тот или иной резистор на суммирующую точку операционного усилителя. Величины токов задаются значениями сопротивлений, номиналы которых уменьшаются в два раза при переходе от младшего разряда к последующему более старшему разряду. Если бит соответствующего разряда равен единице, то ключ S_i подсоединяет цепь тока к суммирующей точке ОУ, в противном случае при нулевом значении бита цепь тока этого разряда разорвана.

Этот принцип по­строения преобразо­ва­ния следует приме­нить и при разра­бот­ке ЦАП для троич­ной системы счисле­ния. Принципиаль­ная схема устройства представлена на рис.13.11.

Рис.13.11. Принципи­аль­ная схема ЦАП для троичной системы счи­-

сления

В системе счи­сления с ос­но­ванием n используются циф­ры от нуля до (n-1), то есть в нашем слу­чае 0,1,2. Преоб­ра­зуемый код заносит­ся в ре­гистр ЦАП, и вес разряда при пере­ходе от нулевого млад­­­ше­го к после­дующему старше­му определяется последователь­ностью 3⁰, 3¹, … 3^n-1. В каждом i-ом разряде преобразуемого кода может находиться одна из цифр набора 0,1,2 при общем количестве разрядов n. В зависимо­сти от величины цифры младшего нулевого разряда переключатель S₀ устанавливается в одно из трёх положений: нижнее (цифра 0), среднее (цифра 1) и верх­нее (циф­ра 2). Совокупность цифр разряда реализуется набором из трёх резисто­­ров – R₀₀, R₀₁, R₀₂ (здесь и далее в индексах резисторов первая цифра указывает на номер реализуемого разряда, второй символ определяет моделируемую цифру набора). Нулевое значение млад­­­шей цифры моделируется тем, что выход нижнего резистора группы R₀₀=R подсоединён к земле. Величины остальных двух резисторов группы цифр младшего разряда устанавливаются из следующих соображений. Наличие единичного сигнала на среднем резисторе R₀₁ группы младшего разряда, моделирующего цифру 1, должно вызывать появление на выходе ОУ напряжения, эквивалентного единице. Следовательно, коэффициент передачи ОУ по этому каналу дол­жен быть равен единице, и тогда на основании выражения (5.3) R₀₁=R. По аналогии наличие единичного сигнала на резисторе R₀₂ группы млад­шего разряда, моделирующего цифру 2, должно вызывать появление на выходе ОУ напряжения, эквивалентного двум. Поэтому коэффициент передачи по этому каналу должен быть равен двум, и на основании (5.3) R₀₂=R/2.

Переход к моделированию цифр первого разряда должен учитывать вес этих цифр, равный 3¹. Здесь и далее ситуация с резисторами R₁₀, R₂₀, …остаётся неизменной – они подключены к земле через резистор R. Сигнал на входе резистора R₁₁ должен приводить к появлению на выходе ОУ напряжения, эквивалентного 3¹, поэтому коэффициент передачи канала должен быть равен трём, и R₁₁=R/3. Сигнал на входе резистора R₁₂ должен вызывать появление на выходе ОУ напряжения, эквивалентного шести. Тогда R₁₂=R/6.

Далее всё повторяется с увеличением весов последующих разрядов в три раза и снижением сопротивлений резисторов в три и шесть раз. Получили схему ЦАП для троичной системы счисления на взвешенных резисторах (рис.13.11), которая полностью повторяет недостатки аналогичной схемы для двоичной системы счисления.

Контрольные вопросы

1. Назначение, классификация цифро-аналоговых преобразователей, основные их характеристики?

2. Последовательные ЦАП: с широтно-импульсной модуляцией, на переключаемых конденсаторах – схемные реализации, их работа, основные соотношения, применение?

3. Параллельные ЦАП: преобразователи с суммированием весовых токов – схемное построение, основные соотношения, практическая реализация, метрологические характеристики?

4. Параллельные ЦАП: преобразователи на матрице R-2R - схемное построение, основные соотношения, практическая реализация, метрологические характеристики?

5. ЦАП на источниках тока - схемное построение, основные соотношения, практическая реализация, метрологические характеристики?

6. Принципы построения ЦАП для троичной системы счисления?

Лекция14. Аналого-цифровые

Преобразователи

Виды аналого-цифровых преобразователей и их особенно­сти. Ана­лого-циф­ровые преобразователи (АЦП) представляют со­­бой устройства, предназначенные для преобразования электричес­ких величин (напряжения, тока, мощности, сопро­тивления, емкости и др.) в цифровой код [1,2,5,9,10,11]. Наиболее часто входной величиной являет­ся напряжение. Все другие величины перед подачей на такой АЦП нужно предварительно преобразовывать в на-пряжение. Однако на практике находят применение также преобра-зователи, например, сопротивления или емкости в циф­ровой код без проме­жу­точного преобразования в напряжение. Обычно это по­зволяет умень­­­шить погрешность преобразования, но усложняет проектиро­вание преобразователя и его изготовление. Последнее объясняется тем, что серийные промышленные микросхемы АЦП предназначены только для работы с напряжением. Поэтому в дальнейшем будут рассмотрены только преобразователи напряжения в цифровой код.

В общем случае напряжение характеризуется его мгновенным значением u(t). Однако для оценки напряжения можно также пользоваться его средним за выбранный промежуток времени Т значением:

.

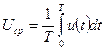В связи с этим все типы АЦП можно разделить на две группы: АЦП мгновен­ных значений напряжения и АЦП средних значений напряжения. Так как операция усреднения предполагает интегрирование мгновенного значения напряжения, то АЦП средних значений часто называют интегрирующими.

При преобразовании напряжения в цифровой код используются три независи­мых операции: дискретизация, квантование и кодирование. Процедура аналого-цифрового преобразования непрерывного сигнала представляет собой преобразо­вание непрерывной функ­­ции напряжения u(t) в последовательность чисел u(t_n), где п=0, 1,2 ... , отнесенных к некоторым фиксированным моментам времени. При дискретизации непрерывная функция u(t) преобразуется в последовательность ее отсчетов u(t_n), как показано на рис.14.1,а.

Вторая операция, называемая квантованием, состоит в том, что мгновенные значения функции u(t) ограничиваются только определенными уровнями, которые называются уровнями квантования. В результате квантования непрерывная функ­ция u(t) принимает вид ступенчатой кривой u_к(t), показанной на рис. 14.1,б.

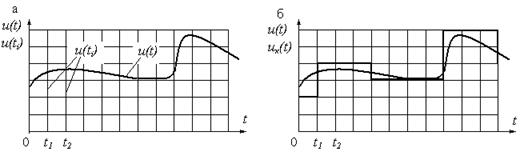
Рис.14.1. Процесс дискретизации (а) и квантования (б) сигнала u(t)

Третья операция, называемая кодированием, представляет дискретные квантованные величины в виде цифрового кода, т.е. последовательности цифр, подчинённых определённому закону. С помощью операции кодирования осуществляется условное представление численного значения величины.

В основе дискретизации сигналов лежит принципиальная возможность представления их в виде взвешенных сумм:

,

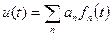где а_n – некоторые коэффициенты или отсчёты, характеризующие исходный сигнал в дискретные моменты времени, f_n(t) – набор элементарных функций, используемый при восстановлении сигнала по его отсчётам.

Дискретизация бывает равномерная и неравномерная. При равномерной дискретизации период отсчётов Т остаётся постоянным, а при неравномерной – период может изменяться. Неравномерная дискретизация чаще всего обусловлена скоростью изменения сигнала и потому называется адаптивной.

В основе равномерной дискретизации лежит теорема отсчётов, согласно которой в качестве коэффициентов а_n нужно использовать мгновенные значения сигнала u(t_n) в дискретные моменты времени t_n=Tn, а период дискретизации выбирать из условия T=(2f_m)^-1, где f_m- максимальная частота в спектре исходного сигнала.

Для сигналов с ограниченным спектром теорема отсчётов имеет вид

и называется формулой Котельникова.

При дискретизации сигнала появляется погрешность, обусловленная конечным временем одного преобразования и неопределенностью момента времени его окончания. В результате вместо равномерной дискретизации получаем дискретизацию с переменным периодом. Такая погрешность называется апертурной. Если считать, что апертурная погрешность определяется скоростью изменения сигнала, то ее можно определить по формуле

,

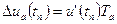где T_a- апертурное время, u’(t_n) - скорость изменения сигнала в момент времени t_n, т. е.

.

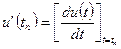Для гармонического сигнала u(t)=U_msinωt максимальное значение апертур­ной погрешности получим при условии u'(t) = U_m, т. е. при cosωt = 1. Относительная апертурная погрешность в этом случае будет иметь значение

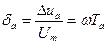. (14.1)

Сравнивая период дискретизации, определенный по теореме отсчетов, с апертурным временем (14.1), получим

,

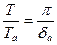откуда следует, что для снижения апертурной погрешности приходится в 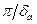раз увеличивать частоту преобразования АЦП. Так, например, при дискретизации гармонического сигнала с частотой f_m=10кГц по теореме отсчетов достаточно иметь максимальную частоту АЦП F_m =2f_т=20 кГц; при погрешности δ_a= 10^-2 необходимо увеличить эту частоту до значения 2f_тπ/δ_a=20·10³π/10^-2 = 6,3МГц.

В отличие от дискретизации, которая теоретически является обратимой операцией, квантование представляет собой необратимое преобразование исходной последовательности и сопровождается появлением неизбежных погрешностей. Характеристика идеального квантователя приведена на рис.14.2,а. При равномерном квантовании расстояние между двумя соседними значениями делается постоянным, как показано на рис. 14.1,б. Разность между двумя соседними значениями квантованной величины называется шагом квантования h.

Рис.14.2. Характеристика иде­­­­аль­ного квантователя (а) и гра­фик изменения погреш-­

ности кван­тования (б)

По существу кванто­вание представляет собой опе­рацию округления непрерывной величины до ближайшего целого значения. В результате максимальная погрешность квантования равна ±0,5h (рис. 14.1,6). Однако при преобразовании произвольного сигнала максимальная погрешность встречается сравнительно редко, поэтому в большинстве случаев для оценки качества АЦПиспользуют не максимальную, а среднеквадратическую погрешность δ_кв=h/ 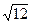, которая примерно в 3,5 раза меньше максимальной. В АЦПпогрешность квантования определяется как единица младшего значащего разряда (ЕМР).

Выходной величиной АЦПявляется цифровой код, т. е. последовательность цифр, с помощью которой представляются дискретные кантованные величины. В АЦПиспользуют четыре основных типа кодов: натуральный двоичный, деся­тичный, двоично-десятичный и код Грея. Кроме этого, АЦП,предназначенные для вывода информации в десятичном коде, выдают на своем выходе специализированный код для управления семисегментными индикаторами.

Большинство АЦПработают с выходом в натуральном двоичном коде, при котором каждому положительному числу N ставится в соответствие код ,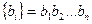

где b_i равны нулю или единице. При этом положительное число в двоичном коде имеет вид

. (14.2)

Такой код принято называть прямым: его крайний правый раз­­ряд является млад­шим, а крайний левый - старшим. Прямой код пригоден лишь для работы с однополярными сигналами. Полный диапазон преобразуемого сигнала равен 2ⁿ, а N_max=2ⁿ-1.

Двоичные числа, используемые в АЦП,как правило, нормализованы, т. е. их абсолютное значение не превышает единицы. Они пред­ставляют собой отношение входного сигнала к полному диапазону:

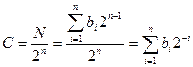. (14.3)

Если АЦПдолжен работать с двуполярными числами, то наиболее часто используют дополнительный код, который образуется вычитанием преобразуемого числа С из постоянной величины 2ⁿ⁺¹. Ина­­че говоря, находится допол­нение до двух к числу С. Диапазон представления чисел в двоичном коде имеет пределы от 2^–m до 1-2^-m. Нуль имеет одно значение 000 ... 0.

При использовании в АЦПдвоично-десятичных кодов каждая значащая десятичная цифра представляется четырьмя двоичными зна­ками и содержит десять значений сигнала от О до 9. Так, например, десятичное число 10 можно представить как 0001 0000, а число 99 можно представить в виде 1001 1001.

Так как при кодировании четырьмя двоичными знаками можно получить 16 кодовых значений, то приведенное двоично-десятич­ное представление не является единственным. Наиболее широко ис­пользуют коды, в которых цифрам в тетрадах присваивают веса 8-4-2-1 или 2-4-2-1:

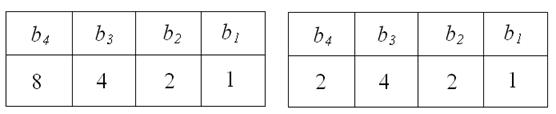
1.

Основные характеристики АЦП.Любой АЦП является сложным электронным устройством, которое может быть выполнено в виде одной интегральной микросхемы или содержать большое количество различных электронных компонентов. В связи с этим характеристики АЦП зависят не только от его построения, но и от характеристик элементов, которые входят в его состав. Тем не менее, большинство АЦП оценивают по их основным метрологическим показателям, которые можно разделить на две группы: статические и динамические.

К статическим характеристикам АЦП относят: абсолютные значения и полярности входных сигналов, входное сопротивление, значения и полярности выходных сигналов, выходное сопротивление, значения напряжений и токов источников питания, количество двоичных или десятичных разрядов выходного кода, погрешности преобразования постоянного напряжения и др. К динамическим параметрам АЦП относят: время преобразования, максимальную частоту дискретизации, апертурное время, динамическую погрешность и др.

Рассмотрим некоторые из этих параметров более подробно. Основной характеристикой АЦП является его разрешающая способность, которую принято определять величиной, обратной максимальному числу кодовых комбинаций на выходе АЦП. Разрешающую способность можно выражать в процентах, в количестве разрядов или в относительных единицах. Например, 10-разрядный АЦП имеет разрешающую способность (1024)^-1»10^-3=0,1%. Если напряжение шкалы для такого АЦП равно 10В, то абсолютное значение разрешающей способности будет около 10мВ.

Реальное значение разрешающей способности отличается от расчетного из-за погрешностей АЦП. Точность АЦП определяется значениями абсолютной погрешности, дифференциальной и интегральной нелинейности. Абсолютную погрешность АЦП определяют в конечной точке характеристики преобразования, поэтому ее обычно называют погрешностью полной шкалы и измеряют в единицах младшего разряда.

Дифференциальную нелинейность (DNL) определяют через идентичность двух соседних приращений сигнала, т. е. как разность напряжений двух соседних квантов: DNL=h_i-h_i+1. Определение дифференциальной нелинейности показано на рис.14.3,а.

Рис.14.3. Определе­ние дифференци­аль­ной (а) и интег­раль­ной (б) нели­­­нейнос-

­тей

Интегральная нелинейность АЦП (INL) характеризует идентичность приращений во всем диапазоне входного сигнала. Обычно ее определяют, как показано на рис.14.3,б, по максимальному отклонению сглаженной характеристики преобразования от идеальной прямой линии, т. е. INL=u_i’-u_i.

Время преобразования T_пр обычно определяют как интервал времени от начала преобразования до появления на выходе АЦП устойчивого кода входного сигнала. Для одних типов АЦП это время постоянное и не зависит от значения входного сигнала, для других АЦП это время зависит от значения входного сигнала. Если АЦП работает без устройства выборки и хранения, то время преобразования является апертурным временем.

Максимальная частота дискретuзации - это частота, с которой возможно преобразование входного сигнала, при условии, что выбранный параметр (например, абсолютная погрешность) не выходит за заданные пределы. Иногда максимальную частоту преобразования принимают равной обратной величине времени преобразования. Однако это пригодно не для всех типов АЦП.

Принципы построения АЦП. Все типы используемых АЦП можно разделить по признаку измеряемого значения напряжения на две группы: АЦП мгновенных значений напряжения и АЦП средних значений напряжения (интегрирующие АЦП). Вначале ознакомимся с АЦП, которые позволяют определять код мгновенного значения напряжения, а затем расс