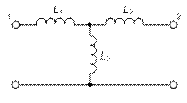
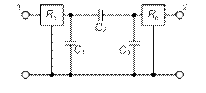
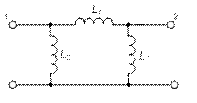
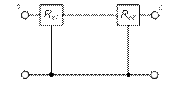
Гираторные схемы индуктивностей

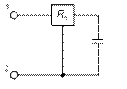
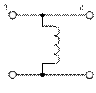
Исходная схема	Гираторная схема	Значение параметров

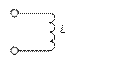
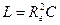
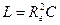
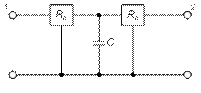
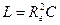
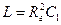
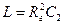
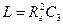
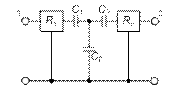
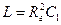
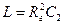
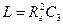
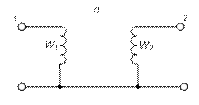
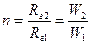
Контрольные вопросы

1. Назначение и виды преобразователей сопротивлений, конверторы и

инверторы сопротивлений и проводимостей, их вольтамперные характеристики. Применение в технике?

2. Моделирование преобразователей сопротивлений и проводимостей на управляемых источниках напряжения или тока: - структурные схемы конверторов, основные соотношения, реализуемость положительных и отрицательных значений сопротивлений?

3. Моделирование преобразователей сопротивлений и проводимостей на управляемых источниках напряжения или тока: - структурные схемы инверторов, основные соотношения, реализуемость положительных и отрицательных значений сопротивлений?

4. Реализация конверторов сопротивлений на управляемых источниках – структурные схемы, основные соотношения, практическое применение?

5. Реализация инверторов сопротивлений на управляемых источниках – структурные схемы, основные соотношения, практическое применение?

6. Устойчивость активных преобразователей сопротивлений и их применение в технике?

Лекция 11. Дифференцирующие и

интегрирующие устройства

Назначение и виды дифференцирующих и интегрирующих устройств [1,2,6,8,9,10]. Дифференцирующим устройством (ДУ) называют такое устройство, сигнал на выходе которого пропорционален производной от входного сигнала, т. е.

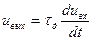, (11.1)

где τ_д— коэффициент пропорциональности, имеющий размер­ность времени.

Простейшее дифференцирующее устройство может быть выполнено на кон­денсаторе или катушке индуктивности. Для кон­денсатора, имеющего емкость С_д, напряжение и ток связаны соот­но­шением (рис.11.1,а):

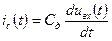, (11.2)

т. е. ток в цепи пропорционален производной от входного напря­же­ния.

Рис.11.1. Ёмкостные дифференцирующие уст­ройства с выходным током (а) и выходным

напряжением (б)

Однако непосредственно использовать эту схему нельзя, так как в ней отсутствует элемент, с которого можно снять выходной сигнал, пропорциональный току i_c(t). Для того, чтобы получить выходной сигнал в виде напряжения, последовательно с конденсатором включают резистор с сопротивлением R_д, т. е. переходят к схеме пос­ледовательного соединения емкости С_д и датчика тока с сопротив­лением R_д, как показано на рис.11.1,б. Введение сопротивления R_д превращает эту цепь в квазидифференцирующую, так как теперь нап­ря­жение и_вх(t)≠и_с(t).

Действительно, для схемы, приведенной на рис. 11.1,б, можно записать, что

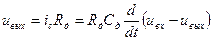, (11.3)

где R_дС_д=τ_д, - постоянная времени дифференцирующего устрой­ства.

Погрешность дифференцирования будет малой, если выполняется условие u_вых<<u_вх, что эквивалентно R_д ®0. В пассивных цепях это условие невыполнимо, поэтому приходится использовать электрон­ные схемы.

Для схемы с индуктивностью L_д можно записать уравнение

,

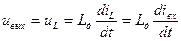откуда следует, что входной сигнал надо подавать в виде тока i_вх(t), а не напряжения u_вх(t), как показано на рис.11.2,а.

Рис.11.2. Индуктивные дифференци­рую­щие устройства с входным током (а) и

входным напряжением (б)

Для того, чтобы преобразовать источник входного напряжения в источник тока, нужно последовательно с ним включить очень боль­шое сопротивление r_д®∞. Однако такая цепь снова станет квазидифференцирующей, а напряжение на индуктивности будет весьма малым (рис.11.2,б). В пассивных цепях это также невыпол­нимо, что приводит к необходимости использовать активные цепи.

Интегрирующим устройством (ИУ) называют такое устройство, сигнал на выходе которого пропорционален интегралу от входного сигнала, т. е.

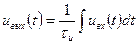,(11.4)

где τ_и — коэффициент пропорциональности, имеющий размер­ность времени.

Простейшие интегрирующие устройства также можно выпол­нить на конденсаторе или катушке индуктивности. Схема простей­ше­го интегрирующего устройства на конденсаторе приведена на рис.11.3,а. Для этой схемы можно записать уравне­ние, связывающее напряжение и ток, в виде:

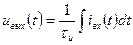(11.5)

откуда следует, что напряжение на емкости С_и пропорционально вход­­ному току i_вх, т. е. входной сигнал должен быть задан в виде тока.

Рис.11.3. Ёмкостные интегрирующие уст­ройства с входным током (а) и выход­­­­-

ным напряжением (б)

Если же входной сигнал задан в виде напряжения u_вх, то для преобразования его в ток необходимо последовательно с источником напряжения включить очень большое сопротивление R_и®∞. При этом выходное напряжение (рис.11.3,б) не будет соответствовать формуле (11.4):

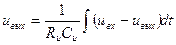, (11.6)

и схема будет квазиинтегрирующей, где R_иC_и=τ_и постоянная времени интеграто­ра. Погрешность интегрирования будет малой, если выпол­нить условие u_вых<<u_вх, что эквивалентно R_и®∞. Поскольку в пассивных цепях это условие выполнить нельзя, то на практике применяют активные электронные схемы.

Схема интегрирующего устройства на индуктивности L_и приведена на рис.11.4, а. Для этой схемы можно написать уравнение

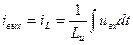, (12.7)

из которого следует, что выходным сигналом является ток i_L=i_вых. Так как токо­вый сигнал нужно преобразовать в выходное напряжение, то последовательно с индуктивностью включается сопротивление r_и, напряжение на котором и является выходным u_r=u_вых.

Рис.11.4. Индуктивные интегрирующие устрой­ства с выходным током (а) и выходным напря­же-

нием (б)

Введение сопротивления r_и делает эту цепь квазиинтегрирующей, и для снижения погрешности выбирается r_и®∞, что приводит к малому значению выходного напряжения. Тем не менее индуктивные интеграторы находят применение, особен­но в трансформаторном включении, когда выходное напряжение снимается не с сопротивления r_и, а со вторичной обмотки трансформатора, индук­тивно связанной с интегрирующей обмоткой.

Рассмотрение простейших дифференцирующих и интегрирую­щих цепей показывает, что для снижения погрешностей и получения выходного напряжения достаточно высокого уровня необходимо использовать активные устройства.

Переходные и частотные характеристики дифференци­рую­щих и интегрирую­щих устройств. Переходная характеристика емкост­ного дифференцирующего уст­ройства может быть найдена из решения дифференциального уравнения (11.3) для схемы, изобра­женной на рис.11.1,б, при условии, что на входе действует скачок напряжения в 1В, т.е. u_вх(t)=1(t). Дифференциальное уравнение цепи

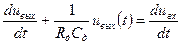(11.7)

при du_вх/dt=0 позволяет найти переходную характеристику в виде

,

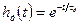где τ_д=C_дR_д - постоянная времени дифференцирующего устройства. График h_д(t) приведен на рис.11.5,а. Очевидно, что при уменьшении сопротивления R_a дли­тельность импульса h_д(t) также уменьшается.

Частотную характеристику дифференцирующего устройства можно постро­ить, если положить, что на входе устройства действует гармоническое напряжение 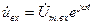. В этом случае по формуле (11.3) находим:

Рис.11.5. Переходная (а) и амплитуд­но-частотная (б) характе­рис­тики диф­фе­ренцирующего устройства

,

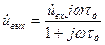откуда получаем значение комплексной передаточной функции

,

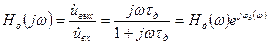где H_д(ω) — амплитудно-частотная характеристика цепи (рис. 11.5,б), а φ_д(ω) - фазо-частотная характеристика.

Для интегрирующего устройства, изображенного на рис.11.3,б, можно записать дифференциальное уравнение

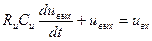, (11.8)

которое позволяет найти переходную характеристику ИУ в виде

,

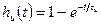где τ_и=C_иR_и — постоянная времени интегрирующего устройства.

Комплексная передаточная функция ИУ определяется выраже­нием ,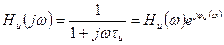

где H_и(ω) и φ_и(ω) — амплитудно- и фазо-частотные харак­теристики ИУ. Графики переходной и амплитудно-частотной харак­теристик ИУ приведены на рис.11.6.

Рис.11.6. Переходная (а) и ам­плитудно-частотная (б) харак­те­рис­тики интегрирующего уст­-

рой­­ства

Емкостные интеграторы с операционными усилителями. Идеальный интегратор с операционным усилителем можно представить в виде схемы, изображением на рис.11.7,а. Если усили­тель обладает характеристиками идеального ОУ т.е. имеет бесконеч­но боль­шое усиление (К_и—>∞), неограниченную полосу пропускания, бесконечно большое входное и бесконечно малое выходное сопротивления, то эквивалентную схему идеального интегратора можно представить в виде, изображенном на рис.11.7,б.

Рис.11.7. Емкостный интегратор с ОУ (а) и его схема замещения (б)

Передаточная функция такого интегратора опреде­ляется формулой

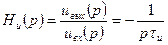,(11.9)

где τ_и=C_иR_и — постоянная времени интегратора.

Переходная характеристика идеального интегратора (реакция на единичный скачок напряжения на входе) в соответствии с (11.3) имеет вид

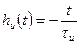, (11.10)

т. е. при скачкообразном напряжении на входе выходное напряжение интегратора изменяется по линейному закону, как показано на рис.11.8,а.

Частотная характеристика идеального интегратора определяется по его пере­даточной функции (11.9) при замене p на jω:

, (11.11)

где H_и(ω) = (ωτ_и)^-1 — амплитудно-частотная характеристика, φ_и(ω) = 90^o — фазовый сдвиг для всех спектральных составляющих входного сигнала.

Графики амплитудно- и фазо-частотной характе­ристик идеального интегра­тора приведены на рис.11.8,а и б. Амплитудно-частотная

Рис.11.8. Переходная харак­те­рис­тика (а) и амплитудно-частотная характеристика (б) интегратора с ОУ

характеристика в лога­риф­ми­ческом масштабе представлена прямой линией со спадом 20 дБ на декаду, а фазо-частотная характеристика — горизонтальной прямой линией φ_и = 90°. В действительности отличие характеристики реального ОУ от характеристик идеального ОУ приводит к значительному изменению свойств емкостного интег­ратора. Во-первых, реальный ОУ имеет конечный коэффициент усиления К_и<∞. Во-вторых, входное и выходное сопротивления ОУ также имеют конечные значе­ния, что особенно сильно сказывается при интегрировании малых токов от источ­ников с большим выходным сопротивлением. И, наконец, операционный усили­тель имеет динамические характеристики, существенно отличные от идеальной модели. Одновременный учет всех этих особенностей реального ОУ приводит к очень сложной схеме замещения, поэтому рассмотрим только влияние ограничен­ного значения коэффициента усиления ОУ, которое будем считать равным К_и.

Пользуясь схемой замещения, приведенной на рис.11.7,б, найдем

,

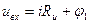где φ₁ — напряжение на входе усилителя.

Напряжение на выходе усилителя u_вых=-K_uφ₁, а напряжение на конденсаторе и_с можно найти как разность φ₁ и u_вых :

.

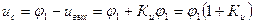В результате определим напряжение на входе ОУ: φ₁ = u_c/(1 +К_u). Так как входной ток ОУ принимаем равным нулю, то ток i=C(du_c/dt), и в результате получаем уравнение для интегратора в виде:

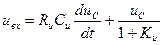или 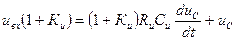.(11.12)

Если сравнить полученное уравнение с уравнением для пассивного RC интег­ратора (11.8)

,

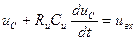то можно сделать вывод, что интегратор на ОУ эквивалентен такой RC-цепи, у которой постоянная времени τ_э = (1+K_u)R_иC_и в (1+К_u) раз больше постоянной времени пассивного интегратора и, кроме того, эквивалентное действующее на­пряжение на входе интегратора тоже увеличено в (1+К_u) раз. Начальная скорость изменения напряжения на конденсаторе осталась неизменной, так как

.

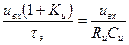Рис.11.9. Переходная характеристика интег­-

ратора на ОУ с ограниченным усилением

На рис.11.9 приведены переходные характеристики пассивной RС - цепи и ак­тивного интегратора на ОУ с ограни­чен­ным усилением, из сравнения которых можно сделать вывод, что погрешность активного интегратора значительно меньше пассивного даже при ограниченном усилении ОУ.

Интеграторы малых и сверхмалых токов. Измерение малых токов, электрических зарядов и сопротив­лений изоляции связано с интегри­рованием очень малых токов, так как непосредственное измерение этих токов или зарядов весьма затруднительно. При этом использу­ется определение заряда на образцо­вом конденсаторе С_к, создаваемого током I_и за некоторое время t_и. Чувствительность таких устройств тем выше, чем меньше емкость об­разцового конденсатора С_к и чем за большее время t_и выполняется интегрирование.

Для снижения входного сопротивления интеграторов тока и снижения по­грешности образцовый конденсатор С_к включают в цепь отрицательной обратной связи, как показано на рис.11.10, где К_и — коэффициент усиления, β — коэф­фициент передачи цепи обратной связи. Применение конденсатора в качестве образцового элемента позволяет достичь более высокой точности, так как погрешность аттестации и нестабильность емкости образцовых конденсаторов значительно меньше, чем для высокоомных резисторов, которые используются для этой же цели.

Рис.11.10. Схема интегратора малых токов

Простейшие интеграторы тока пред­став­ляют собой циклические устройства, в которых после каждого цикла заряда накопительного конденсатора С_к требует­ся возвращение схемы в исходное состояние, т. е. требуется разряд интегрирующе­го конденсатора. Иногда для получения текущего значения тока на выходе интег­ратора включают дифференцирующее устройство в виде простейшей RС - цепи или операционного дифференцирующего усилителя.

Для того чтобы в схеме соблюдался режим интегрирования, необходимо выполнение условия t_и<<τ_вх , где τ_вх = C_вх/g_вх — постоянная времени входной цепи интегратора. При большом коэффициенте усиления τ_вх почти полностью опреде­ляется постоянной времени цепи обратной связи

Выходное напряжение интегра­тора при ступенчатом токе I_и определяется его переходной ха­рактеристикой

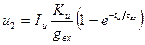.(11.13)

При большой постоянной времени τ_вх>>t_и это выражение можно разложить в степенной ряд Тейлора и, ограничиваясь двумя членами ряда, записать выходное напряжение в виде

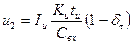, (11.14)

где δ_τ = t_и/2τ_вх — погрешность нелинейности интегратора.

Эта погрешность интегратора уменьшается с увеличением постоянной време­ни входной цепи. Однако максимальное значение τ_вх не может превышать посто­янной времени цепи обратной связи C_к/g_к.

Для получения выходного напряжения, пропорционального текущему значе­нию входного тока I_и, можно использовать дифференцирующее устройство, уста­новленное на выходе интегратора. Схема интегратора тока с дифференцирующим звеном приведена на рис. 11.11.

Рис.11.11. Интегратор тока с дифферен­ -

ци­рующим звеном

Для схемы интегратора тока с дифференцирующим звеном можно получить значение выходного напряжения, аналогичное (11.14), при условии замены t_и на τ_д:

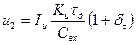. (11.15)

Сравнивая выражения (11.15) и (11.14), можно сделать вывод, что чувстви­тельность интегратора с дифференцирующим звеном на выходе интегратора ниже, так как τ_д<t_и.

Как уже отмечалось, в интеграторах малых токов используют интегрирую­щие конденсаторы малой емкости (от 10 до 50 пФ). Это позволяет увеличить чув­ствительность интегратора, но снижает допустимое время интегрирования. Для увеличения времени интегрирования применяют автоматическую компенсацию зарядного тока.

Схема интегратора с автокомпенсацией зарядного тока приведена на рис.11.12. Выходное напряжение интегратора через интегрирующую цепь R_иС_и подводится к образцовому конденсатору С_к, создавая компенсирующий ток.

Коэффициент передачи звена обратной связи имеет значение

Рис.11.12. Интегратор тока с автокомпенсацией зарядного тока

,

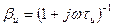где τ_и = R_иC_и — постоянная времени интегрирующей цепи.

При достаточно боль­шой постоянной времени τ_и интегрирующего звена обратной связи время ин­тегрирования увеличива­ется больше, чем в два раза. Постоянная времени интегратора тока опреде­ляется в основном каче­ством интегрирующего конденсатора С_к. При исполь­­зо­­вании конденсаторов с воздушным диэлектриком прово­димость утечки g_к в основном определяется опорными изолятора­ми, к которым крепятся пластины конденсатора, как показано на рис. 11.13,а.

Рис.11.13. Способы включения накопи­тель­ного конденсатора: без охранного электрона (а) и с охранным электро­ -

дом (б)

Для увеличения постоянной времени интегратора при использовании конденсаторов с воздушным диэлектриком можно применить охранный электрод, который отводит токи утечки по опорному изолятору на корпус. Охранный электрод помещается между опорными изолято­рами и соединяется с общей шиной усилителя, как показано на рис.11.13,б. При этом проводимость g_к между входным опорным изолятором и охранным электро­дом оказывается включенной параллельно g₁ , а постоянная времени интегратора увеличивается примерно в К_иβ раз.

Конструктивное выполнение конденсаторов интегратора малых токов с ох­ранным электродом приведено на рис.11.14. Наибольшее распространение полу­чили конденсаторы с односторонними выводами, изображенные на рис.11.14,а, и конденсаторы с двухсторонними выводами, изображенные на рис.11.14,б. Охран­ное кольцо размещается на стороне выхода интегратора и подключается к обще­му проводу. Основные характеристики накопительного конденсатора типа НК-2, используемого в интеграторе электрометра ВК2-16, имеют следующие значения: С_к=100пФ; R_из=10¹⁵Ом, погрешность 1%.

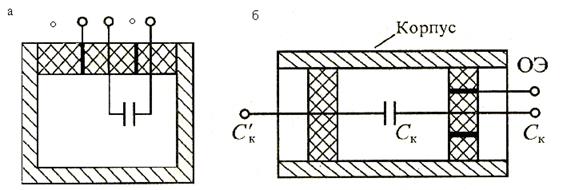
Рис.11.14. Конструкции конденсаторов с охранным электродом: с односторонними выводами (а) и с двусторонними выводами (б)

Дифференцирующие устройства на операционных усилителях. Идеальное диф­ференцирующее устройство с операционным усилителем можно представить в виде схемы, изображенной на рис. 11.15,а. Схема замещения дифференцирующего устройства с идеальным ОУ приведена на рис.11.15,б.

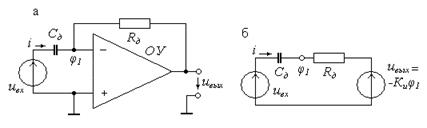
Рис.11.15. Емкостное дифференцирующее устройство на ОУ (а) и его

схема замещения (б)

Передаточная функция такого ДУ определяется формулой

,

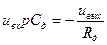откуда 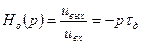, (11.16)

где 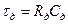- постоянная времени дифференцирующего устройства.

Переходная характеристика идеального ДУ в соответствии с (11.16) определя­ется зависимостью

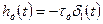, (11.17)

где δ_l(t) — импульсная функция первого рода. Таким образом, при скачкообраз­ном напряжении на входе ДУ выходное напряжение будет иметь форму очень короткого импульса (теоретически его длительность равна нулю). График пере­ходной характеристики ДУ приведен на рис.11.16,а.

Частотная характеристика ДУ определяется по его передаточной функции (11.16) при замене ρ=jω :

,

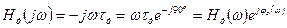где 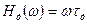- амплитудно-частотная характеристика ДУ, а 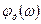= -90° — фазовый сдвиг (фазо-частотная характеристика). Графики амплитудно-частотной и фазо-частотной характеристик ДУ приведены на рис.11.16,б.

Рис.11.16. Переходная харак­те­ристика (а) и амплитудно-частотная характеристика (б)

дифференци­рующего устройства на ОУ

Дифференциатор на реальном ОУ отличается от идеального ДУ тем, что его результирующая частотная характеристика имеет два полюса и один нуль, что указывает на возможность его самовозбуждения. При этом один полюс определя­ется собственной АЧХ ОУ. Для увеличения устойчивости дифференциатора па­раллельно R_д иногда включают корректирующий конденсатор С_к.

Полное входное сопротивление дифференциатора имеет емкостный характер, так как Z_вх = (ωC_д)^-1, поэтому с увеличением частоты входное сопротивление уменьшается и растет ток, потребляемый ДУ от источника сигнала. Для ограниче­ния входного тока последовательно с емкостью С_д можно включить сопротивле­ние R_к. Полная схема ДУ с дополнительными корректирующими элементами приведена на рис.11.17.

Рис.11.17. Схема дифференциатора на ОУ с внешней коррекцией

Дифференцирующие устройства нахо­дят широкое применение в формировате­лях импульсов, в активных фильтрах, в генераторах колебаний и других случаях.

Контрольные вопросы

1. Ёмкостные и индуктивные дифференцирующие устройства – схемные реализации, основные соотношения, погрешности преобразования?

2. Ёмкостные и индуктивные интегрирующие устройства - схемные реализации, основные соотношения, погрешности преобразования?

3. Переходные и частотные характеристики дифференцирующих и интегрирующих устройств – основные соотношения, графические построения переходных и амплитудно-частотных характеристик?

4. Ёмкостные интеграторы с операционными усилителями – схемная реализация, основные соотношения, графики переходной, амплитудно- и фазо-частотной характеристик.

5. Интеграторы малых и сверхмалых токов – схемные реализации, основные соотношения, сравнительные данные по конструктивным исполнениям.

6. Дифференцирующие устройства на операционных усилителях – схемная реализация, основные соотношения, переходная и амплитудно-частотная характеристики? Реализация внешней коррекции?