Основные акустические свойства сред
| Материал | Плотность r, г /см3 | Скорость упругих волн с, м/с | Характеристический импеданс, 106 г/смс | Длина волны l при f = 2,5 МГц, мм | |||
| Сl | Ct | Zl | Zt | прод. | попереч. | ||
| Дюралюминий | 2,7 | 1,69 | 0,84 | 2,5 | 1,24 | ||
| Вода | 1,0 | – | 0,15 | – | 0,6 | – | |
| Воздух | 0,0013 | – | 4´10–7 | – | 0,13 | – | |
| Масло | 0,90 | – | 0,9 | – | 0,55 | – | |
| Медь | 8,9 | 4,15 | 2,01 | 1,9 | 0,9 | ||
| Оргстекло | 1,18 | 0,32 | 0,13 | 1,1 | 0,45 | ||
| Сталь углеродистая | 7,8 | 4,6 | 2,54 | 2,4 | 1,3 | ||
| Сталь нержавеющая | 8,0 | 4,54 | 2,51 | 2,3 | 1,25 |
2.3.Отражение и прохождение волн на границах сред
Если упругая волна падает на границу раздела двух сред, то могут происходить несколько явлений: отражение, преломление и трансформация волн.
Отражением называется изменение направления распространения волны на границе раздела, при котором волна не переходит в другую среду. Преломлением называется изменение направления и (или) скорости волны на границе раздела, при котором волна переходит в другую среду. Трансформацией называют преобразование типа или поляризации волн, происходящее на границе раздела двух сред. Например, падающая объемная волна может преобразоваться в поверхностную волну Рэлея (преобразование типа волны), либо продольная волна может преобразоваться в поперечную (преобразование поляризации).
Сначала рассмотрим падение плоской объемной волны на плоскую гладкую границу двух сред, рис.2.9. Пусть, для определенности, падающая из среды 1 волна имеет продольную поляризацию. В общем случае от границы раздела отражаются две волны: продольная и поперечная, преломляются и проходят в среду 2 тоже две волны – одна продольная, другая поперечная. Введем углы падения 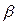 , отражения
, отражения 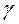 и преломления
и преломления 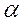 . Каждый из этих углов измеряется между направлением распространения соответствующей волны и перпендикуляром, восстановленным в точке падения. Так, угол падения на рис. 2.9 – это
. Каждый из этих углов измеряется между направлением распространения соответствующей волны и перпендикуляром, восстановленным в точке падения. Так, угол падения на рис. 2.9 – это 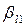 , углы отражения
, углы отражения 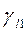 ,
, 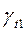 и углы преломления
и углы преломления 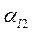 и
и 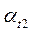 .
.
 Первый индекс означает тип или поляризацию волны, второй – номер среды. Скорости, с которыми распространяются волны, указаны на рис. 2.9 у падающего, отраженных и преломленных лучей. Задача, которую нам предстоит решить, заключается в следующем. Допустим, нам известны угол падения
Первый индекс означает тип или поляризацию волны, второй – номер среды. Скорости, с которыми распространяются волны, указаны на рис. 2.9 у падающего, отраженных и преломленных лучей. Задача, которую нам предстоит решить, заключается в следующем. Допустим, нам известны угол падения 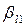 и амплитуда Аи падающей волны. Требуется определить углы, под которыми распространяются отраженные и преломленные волны и их амплитуды.
и амплитуда Аи падающей волны. Требуется определить углы, под которыми распространяются отраженные и преломленные волны и их амплитуды.
Для падающей, отраженных и преломленных волн отношение синуса угла (между направлением распространения и нормалью к поверхности раздела) к скорости волны есть величина постоянная. Это закон отражения и преломления или закон Снеллиуса. Его математическое выражение
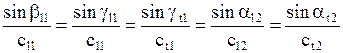 . (2.16)
. (2.16)
Поскольку скорости продольных падающей и отраженной волн в первой среде равны, то из (2.16) равны и углы падения и отражения: 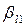 =
= 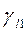 . Отношение скоростей преломленной спр. и падающей спад. волн – это коэффициент преломления п:
. Отношение скоростей преломленной спр. и падающей спад. волн – это коэффициент преломления п:
n= спр/спад. (2.17)
Чем больше скорость прошедшей (преломленной) волны, тем больше угол преломления. Поэтому преломленная продольная волна отклонена от нормали больше, чем поперечная. Для того чтобы знать, каким образом реализуется явление преломления, очень важно соотношение между скоростями волн в первой и второй средах. Выберем для рассмотрения какую-либо одну из преломленных волн.
Возможны три случая: спр > спад.; спр<спад и спр=спад. В последнем случае преломления луча на границе раздела не происходит. Первый и второй случаи иллюстрирует рис. 2.10.
Пунктирной линией показано мысленное продолжение падающего луча во вторую среду. Случай «а» соответствует падению волны из среды с большей скоростью в среду с меньшей скоростью (например, из стали в оргстекло). Луч преломленной волны всегда находится между пунктирной линией и нормалью к границе раздела. При увеличении угла падения 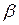 от нуля до 90° преломленная волна существует всегда. Иное положение в случае «б», когда волна падает из среды с меньшей скоростью в среду с большей, например из оргстекла в сталь. В этом случае угол преломления
от нуля до 90° преломленная волна существует всегда. Иное положение в случае «б», когда волна падает из среды с меньшей скоростью в среду с большей, например из оргстекла в сталь. В этом случае угол преломления 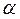 больше угла падения
больше угла падения 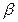 . При увеличении
. При увеличении 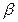 обязательно настанет момент, когда преломленная волна пойдет параллельно поверхности. Говорят, что в этом случае волна падает под критическим углом. В контроле УЗ вводятся три критических угла. Рассмотрим их более подробно.
обязательно настанет момент, когда преломленная волна пойдет параллельно поверхности. Говорят, что в этом случае волна падает под критическим углом. В контроле УЗ вводятся три критических угла. Рассмотрим их более подробно.
а б
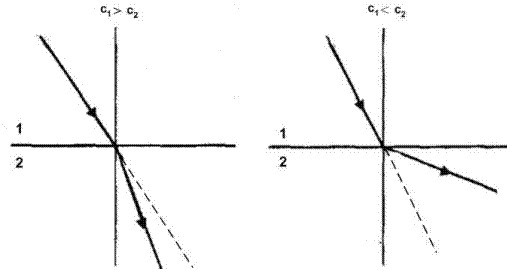
Рис. 2.10. Ход лучей при падении: а – с1> с2; б –с1<с2
Угол падения, при котором преломленная продольная волна выходит на поверхность раздела сред, называется первым критическим углом, 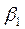 . Преломленная волна при этом превращается в головную. При значениях угла падения, превышающих
. Преломленная волна при этом превращается в головную. При значениях угла падения, превышающих 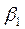 , во второй среде продольная волна отсутствует.
, во второй среде продольная волна отсутствует.
Угол падения, при котором преломленная поперечная волна выходит на поверхность раздела сред, называется вторым критическим углом, 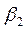 . Преломленная поперечная волна при этом превращается в поверхностную волну Рэлея. При значениях угла падения, превышающих
. Преломленная поперечная волна при этом превращается в поверхностную волну Рэлея. При значениях угла падения, превышающих 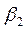 ,объемные однородные волны во второй среде отсутствуют.
,объемные однородные волны во второй среде отсутствуют.
Значения критических углов для границы оргстекло-сталь таковы: 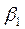 =27,5° ,
=27,5° , 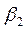 = 56° – 57°.
= 56° – 57°.
Угол падения поперечной волны, при котором отраженная продольная волна выходит на поверхность, называется третьим критическим углом 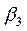 . Для стали этот угол равен 33°.
. Для стали этот угол равен 33°.
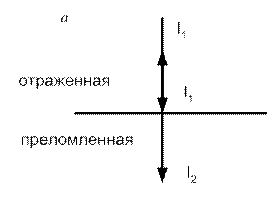
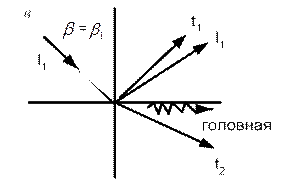
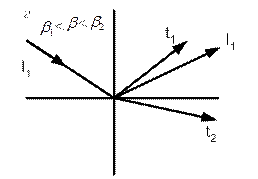
На рис. 2.11 схематично показано, какие волны возникают во второй среде при падении продольной волны при спад<спр. Случай нормального падения  =0 показан на рис. 2.11, а. В этом случае видимого преломления лучей нет; падающая, отраженная и преломленная волны направлены по нормали к поверхности раздела. Трансформации волн тоже нет. При значении угла падения, которое меньше первого критического, во второй среде есть две преломленные волны – продольная и поперечная (рис. 2.11, б). Случай падения под первым критическим углом показан на рис. 2.11, в. Вместо вышедшей на поверхность продольной преломленной волны образуется головная. Если
=0 показан на рис. 2.11, а. В этом случае видимого преломления лучей нет; падающая, отраженная и преломленная волны направлены по нормали к поверхности раздела. Трансформации волн тоже нет. При значении угла падения, которое меньше первого критического, во второй среде есть две преломленные волны – продольная и поперечная (рис. 2.11, б). Случай падения под первым критическим углом показан на рис. 2.11, в. Вместо вышедшей на поверхность продольной преломленной волны образуется головная. Если 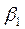 <
< 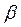 <
< 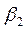 , то во второй среде есть только поперечная волна (рис. 2.11, г). Наконец, при
, то во второй среде есть только поперечная волна (рис. 2.11, г). Наконец, при 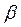 >
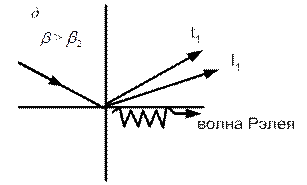
> 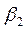 (рис. 2.11, д) объемных волн во второй среде нет, а вдоль границы раздела бежит поверхностная волна.
(рис. 2.11, д) объемных волн во второй среде нет, а вдоль границы раздела бежит поверхностная волна.
| 
|
| 
|
| Рис. 2.11. Отражение, преломление и трансформация волн при разных углах падения |
|
Дата добавления: 2020-04-12; просмотров: 812;











