Методы Рунге-Кутты произвольного и четвертого порядков

Любой метод из семейства методов Рунге-Кутты второго порядка (21) реализуют по следующей схеме. На каждом шаге, т.е. при каждом i = 0, 1, 2, ..., вычисляют значения функции

, ,

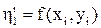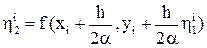а затем находят шаговую поправку

,

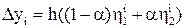прибавление которой к результату предыдущего шага дает приближенное значение решения у(x) в точке x_i+1 = x_i + h:

y_i+1 = y_i + Dy_i.

Метод такой структуры называют двухэтапным по количеству вычислений значений функции правой части уравнения (1) — на одном шаге.

Анализ устройства методов Рунге-Кутты второго порядка позволяет представить, в какой форме следует конструировать явный метод Рунге-Кутты произвольного порядка. По аналогии с предыдущим для семейства методов Рунге-Кутты p-го порядка используется запись, состоящая из следующей совокупности формул:

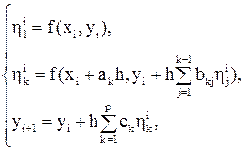(23)

где k = 2, 3, …, p (для p-этапного метода). Многочисленные параметры c_k, a_k, b_k, фигурирующие в формулах (23), подбираются так, чтобы получаемое методом (23) значение y_i+1 совпадало со значением разложения y(x_i+1) по формуле Тейлора с погрешностью O(h^p+1) (без учета погрешностей, совершаемых на предыдущих шагах).

Наиболее употребительным частным случаем семейства методов (23) является следующий метод Рунге-Кутты четвертого порядка, относящийся к четырехэтапным и имеющий вид:

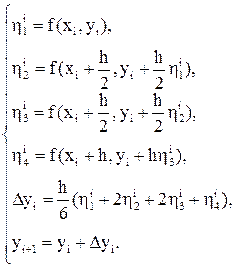(24)

Заметим, что если первый этап, как уже упоминалось, соответствует применению явного метода Эйлера, то четвертый — неявного, а второй и третий — уточненного методов Эйлера. Последний имеет более высокий порядок точности, отсюда и больший вес отвечающих ему значений этапных поправок.