Модификации метода Эйлера

Численные методы решения дифференциальных уравнений

Задача Коши

Будем рассматривать обыкновенное дифференциальное уравнение (ОДУ) первого порядка

y' = f(x, y), x Î [x₀; b] (1)

с начальным условием

y(x₀) = y₀, (2)

где f(x, у) — некоторая заданная, в общем случае, нелинейная функция двух переменных. Будем считать, что для данной задачи (1)-(2), называемой начальной задачей или задачей Коши, выполняются требования, обеспечивающие существование и единственность на отрезке [x₀; b] ее решения y = y(x) (такие требования можно найти в любом курсе дифференциальных уравнений или в соответствующем разделе курса высшей математики). Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и «законного» применения того или иного метода.

Несмотря на внешнюю простоту уравнения (1), решить его аналитически, т. е. найти общее решение y = y(x, C) с тем, чтобы затем выделить из него интегральную кривую y = y(x), проходящую через заданную точку (x₀; y₀), удается лишь для некоторых специальных типов таких уравнений, описание которых также можно обнаружить, например, в упомянутых литературных источниках. Поэтому, как и в родственной для (1)-(2) задаче вычисления интегралов, приходится делать ставку на приближенные способы решения начальных задач для ОДУ, которые можно разделить на три группы:

1) приближенно-аналитические методы,

2) графические или машинно-графические методы,

3) численные методы.

К методам первой группы относят такие, которые позволяют находить приближение решения у(x) сразу в виде некоторой «хорошей» функции φ(x). Например, широко известен метод степенных рядов, в одну из реализаций которого заложено представление искомой функции у(x) отрезком ряда Тейлора, где тейлоровые коэффициенты, содержащие производные высших порядков, находят последовательным дифференцированием самого уравнения (1). Другим представителем этой группы методов является метод последовательных приближений или метод Пикара.

Название графические методы говорит о приближенном представлении искомого решения у(x) на промежутке [x₀; b] в виде графика, который можно строить по тем или иным правилам, связанным с графическим толкованием данной задачи. Физическая или, возможно, точнее будет сказать, электротехническая интерпретация начальных задач для определенных видов уравнений лежит в основе машинно-графических методов приближенного решения. Реализуя на физико-техническом уровне заданные электрические процессы, на экране осциллографа наблюдают поведение решений дифференциальных уравнений, описывающих эти процессы. Изменение параметров уравнений приводит к адекватному изменению поведения решений, что положено в основу специализированных аналоговых вычислительных машин (АВМ).

Наконец, наиболее значимыми в настоящее время, характеризуемое бурным развитием и проникновением во все сферы человеческой деятельности цифровой вычислительной техники, являются численные методы решения дифференциальных уравнений, предполагающие получение числовой таблицы приближенных значений у_i искомого решения y(x) на некоторой сетке x_i Î [x₀; b] значений аргумента x. Этим способам и будет посвящено дальнейшее изложение. Что делать с получаемыми численными значениями решения, зависит от прикладной постановки задачи. Если речь идет о нахождении только значения у(b), тогда точка b включается как конечная в систему расчетных точек x_i, и все приближенные значения y_i » y(x_i), кроме последнего, участвуют лишь как промежуточные, т. е. не требуют ни запоминания, ни обработки. Если же нужно иметь приближенное решение y(x) в любой точке x, то для этого к получаемой числовой таблице значений y_i можно применить какой-либо из способов аппроксимации табличных функций, рассмотренных ранее, например, интерполяцию или МНК. Возможны и другие использования численных данных о решении.

Метод Эйлера

Будем считать, что вычисления проводятся с расчетным шагом 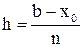, расчетными точками (узлами) служат точки x_i = x₀ + ih (i = 0, 1, ..., n) промежутка [x₀, b] и целью является построение таблицы

приближенных значений y_i решения у = y(x) задачи (1)-(2) в расчетных точках x_i.

Проинтегрируем левую и правую части уравнения (1) в границах от x₀ до x:

.

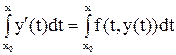Тогда начальную задачу для ОДУ (1)-(2) можно заменить эквивалентным интегральным уравнением

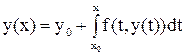
При x = x₁ из него получится равенство

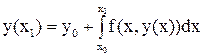(3)

Применение к интегралу в правой части равенства (3) простейшей (одноточечной) формулы левых прямоугольников дает приближенную формулу

y(x₁) » y₀ + f(x₀, y(x₀))(x₁­ – x₀),

В общем случае расчетная формула метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве

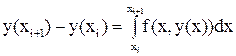(4)

в предположении, что на каждом i-м шаге в роли начальной точки (x₀, y₀) выступает точка (x_i, y_i)

y_i+1 = y_i + hf(x_i, y_i). (5)

Зная точность используемой в (4) квадратурной формулы, легко прийти к выражению ошибки метода Эйлера.

Существуют и другие подходы к выводу метода Эйлера. В частности, он будет возникать далее как частный случай некоторых семейств численных методов решения задачи (1)-(2).

Модификации метода Эйлера

Разовьем последний из подходов к построению метода Эйлера. Очевидно, применение к интегральному равенству (4) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (1)-(2).

Так, если в (4) использовать простейшую квадратурную формулу правых прямоугольников (5.7), придем к методу

y_i+1 = y_i + hf(x_i+1, y_i+1), i = 0, 1, …, n. (6)

Этот метод называют неявным (или обратным) методом Эйлера, поскольку для вычисления неизвестного значения y_i+1 » y(x_i+1) по известному значению y_i » y(x_i) требуется решать уравнение, в общем случае нелинейное. Имеет ли свою сферу применения подобный метод, порядок которого такой же, как и у явного метода Эйлера (14.8) (первый), и один шаг вычислений по которому столь трудоемок? Положительный ответ на этот вопрос будет дан далее.

Применение к интегралу в (4) простейшей квадратурной формулы трапеций приводит тоже к неявному методу

, i = 0, 1, ..., n, (7)

который будем называть методом трапеций. Квадратурная формула трапеций, как известно, на порядок точнее формул левых и правых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (7) по сравнению с явным и с неявным методами Эйлера (5) и (6), т. е. метод трапеций (7) — это метод второго порядка.

Некоторый интерес представляет совместное применение явного метода Эйлера и неявного метода трапеций.

По форме равенство (7) представляет собой скалярную задачу о неподвижной точке относительно неизвестного значения y_i+1. Поэтому, если в правую часть (7) подставить хорошее начальное приближение 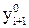, подсчитываемое по формуле (5), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный метод

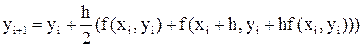, i = 0, 1, …, n, (8)

который называют методом Хойна.

Ясно, что можно достичь большей точности, если, исходя из того же начального приближения

,

сделать не одну, а несколько итераций по методу трапеций:

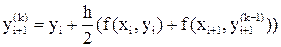, i = 1, 2, ..., n. (9)

Такой вариант совместного применения метода Эйлера и метода трапеций называют усовершенствованным методом Эйлера-Коши с итерационной обработкой. Делать много итераций по формуле (9) не рекомендуется (обычно их выполняют не более трех-четырех). Совпадение определенного числа разрядов в полученных числах и говорит о точности, с которой решено методом простых итераций уравнение (7) относительно y_i+1, а вовсе не о том, что с такой точностью найдено значение y(x_i+1).

Чтобы получить следующую модификацию метода Эйлера, проинтегрируем уравнение (1) по отрезку [x_i–1; x_i+1]. Имеем

,

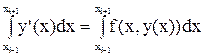откуда следует равенство

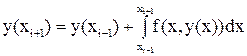. (10)

Применяя к последнему интегралу одноточечную квадратурную формулу средних прямоугольников (12.10) и заменяя значения y(x_i–1) и y(x_i) известными приближенными значениями y_i–1 и y_i соответственно, из (10) выводим формулу для подсчета приближенного значения у(x_i+1)

y_i+1 = y_i–1 + 2hf(x_i, y_i), i = 1, 2, ..., n – 1, (11)

которую будем называть уточненным методом Эйлера.

Как известно, квадратурная формула прямоугольников (средней точки) имеет тот же порядок точности, что и квадратурная формула трапеций, так что уточненный метод Эйлера (11) тоже является методом второго порядка.