ГИДРОДИНАМИЧЕСКИЙ МЕТОД ОЦЕНКИ ЭЗ

Структура фильтрационного сопротивления месторождения:

,

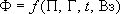где - гидродинамические Параметры водоносной системы,
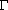- Граничные условия потока,
t - расчетное время развития депрессионной воронки,
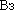- схема и конструкция Водозаборного сооружения.
При применении гидродинамического метода оценки все эти компоненты, интегрально образующие величину , разведуются раздельно, любыми доступными методами и затем раздельно учитываются в расчетных формулах фильтрации к скважинам или вводятся в состав моделей для моделирования работы водозабора.
Поясняющие примеры:
По материалам разведки доказана возможность применения расчетной схемы неограниченного в плане, однородного, изолированного в разрезе пласта; следовательно, расчет понижения уровня в водозаборной скважине можно сделать по формуле Тейса:

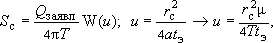
то есть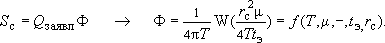
Таким образом, можно видеть, что в условиях "схемы Тейса" величина зависит от гидродинамических параметров 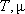, времени эксплуатации 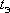и характеристики водозабора 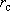. Данные о граничных условиях Г в описании отсутствуют, что вполне понятно для неограниченного пласта.
Другой пример: водозаборная скважина рассчитывается для условий стационарного режима фильтрации в связи с перетеканием из смежного водоносного горизонта:

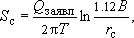
где 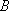- фактор перетекания.
В этом случае 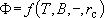; в этом описании фактор перетекания 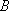является "представителем" граничных условий Г, а время и водоотдача отсутствуют, так как речь идет о стационарном режиме фильтрации.
Такие примеры можно продолжить. Например, для несовершенных водозаборных скважин в величине сопротивления появятся 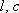- длина фильтра и расстояние от края фильтра до кровли пласта (Вз); если область фильтрации в плане ограничена (выклинивание пласта, фациальное замещение...), то появится расстояние до этой границы 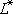(Г). Любое изменение в расчетной схеме отражается в содержании обобщенного фильтрационного сопротивления .

Итак, при использовании гидродинамического метода оценки ЭЗ нужно РАЗДЕЛЬНО РАЗВЕДАТЬ И КОЛИЧЕСТВЕННО ОЦЕНИТЬ ВСЕ КОМПОНЕНТЫ РАСЧЕТНОЙ СХЕМЫ.
После этого подсчет запасов (точнее, расчет водозабора, т.к. подсчет запасов - это более общая задача) выполняется

- или АНАЛИТИЧЕСКИ(по формулам теории притока к скважинам) - при этом формулы выбираются в соответствии с разведанной расчетной схемой, а "начинкой" формул являются разведанные параметры)
- или с использованием МОДЕЛИРОВАНИЯработы водозабора - создается модель МПВ, на которой решается прямая задача с целью получить распределение (во времени и пространстве) напоров (или понижений) при полностью известном (разведанном!) распределении параметров, граничных условий и т.д. (известны все аргументы, ищем функцию).

Во всех случаях для выполнения гидродинамического расчета необходимо составление ФИЛЬТРАЦИОННОЙ СХЕМЫ МЕСТОРОЖДЕНИЯ, которая является конечной целью разведки и должна адекватно, с наилучшей возможной степенью приближения отражать все те гидрогеологические условия, которые в конкретном случае контролируют величину .
Основой для составления фильтрационной схемы являются результаты поисково-разведочных работ: они (работы) должны быть запроектированы, проведены и интерпретированы так, чтобы схема стала достоверной, т.е. содержала бы в себе все те элементы природной обстановки, которые в конкретном случае являютсязначимымидля формирования балансово-гидродинамической ситуации.
Принципы и содержание фильтрационной схематизации гидрогеологических условий для целей любого гидрогеодинамического расчета уже подробно прорабатывались в курсе "Гидрогеодинамика". Здесь мы кратко их повторим, учитывая некоторую специфику расчетов водозаборных сооружений.

Обязательные разделы фильтрационной схематизации,
т.е. вопросы, которые гидрогеолог должен поставить перед собой и обосновать ответ по данным разведки

• Должен быть обоснован ожидаемый РЕЖИМ ФИЛЬТРАЦИИ ВО ВРЕМЕНИ при работе водозабора. Ответ на этот вопрос обосновывается:

- выявленными источниками формирования баланса водоотбора и прогнозируемым временем проявления каждого из них,
- заданным режимом водоотбора (вдруг периодический?)

В зависимости от решения по этому пункту расчетной схематизации прогноз работы водозабора может быть выполнен в стационарном или нестационарном виде - первый вариант проще в исполнении (особенно при моделировании) и требует меньшего числа исходных данных (не нужны емкостные параметры).
Возможность наступления стабилизации депрессии 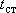в простых случаях можно просчитать аналитически:
- например, если водозабор расположен у реки

,

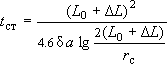где 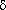- относительная погрешность (по понижениям) признания факта стабилизации; например, при 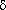= 0.1 стабилизация считается наступившей при 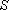= 9 м, хотя "истинная" стабилизация наступит позже, при 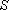= 10 м.

- при наличии перетекания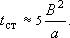

• Должна быть обоснована ожидаемая ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПОТОКАпри работе водозабора, определяемая степенью деформации гидродинамической сетки по пространственным координатам. Ее обоснование производится на основе общих гидрогеодинамических предпосылок:

• конфигурация границ в плане и их положение в разрезе,
• расположение и степень несовершенства водозахватных устройств,
• соотношение мощности пласта и его размеров в плане и др.

Возможные варианты расчетной пространственной структуры течения:

• трехмерная,
• двумерная (в плане или разрезе),
• и даже одномерная (обычно радиальная).

Для упрощения расчетов желательно понизить мерность потока (но обоснованно!). Например, можно использовать предпосылку перетекания - при соотношении коэффициентов фильтрации слоев в слоистых разрезах порядка 20-50 и более (напомнить преломление линий тока по правилу тангенсов) можно реальный пространственный поток рассматривать как плоско-пространственный, что легче в расчетном смысле и проще с точки зрения параметрического обеспечения.

• Характер распределения в плане и разрезе необходимых ПАРАМЕТРОВ ВОДОНОСНОЙ СИСТЕМЫ:

• проницаемость (проводимость для одномерных и плановых потоков или коэффициент фильтрации для профильных и пространственных потоков)
• емкость (водоотдача для моделирования или уровне- пьезопроводность для большинства аналитических решений).

Возможные варианты схематизации выявленного при разведке распределения этих параметров:

а) однородный пласт,
б) квазиоднородный - хаотическое распределение относительно небольших элементов неоднородности с небольшой амплитудой колебания параметра,
в) упорядоченно-неоднородный - при наличии геометрически правильных границ неоднородности (прямая линия, круг, полоса и т.п.) или при наличии функциональной, генетически обусловленной зависимости параметра от природных факторов (мощности пласта, глубины эрозионного вреза и т.п.),
г) существенно-неоднородный - неупорядоченно расположенные крупные элементы неоднородности с контрастными различиями параметра.

Для неоднородных пластов составляются карты параметров с использованием изолиний или по кусочно-неоднородному принципу ("лоскутное одеяло").
Проще для расчетов однородные схемы. При неоднородности, как правило, приходится применять моделирование, так как формулы становятся слишком громоздкими или отсутствуют вовсе.
Важная деталь: по мере удаления от водозабора роль неоднородности (т.е. степень ее влияния на результат расчета - понижения в водозаборе) уменьшается. С максимальной точностью нужно учитывать неоднородность

• в районе расположения водозахватных устройств
• на участках между водозабором и важными границами; для остальной площади обычно можно использовать осредненные значения.

Полезная, но пока слабо разработанная методически вещь: применение так называемых разведочных расчетов (В.М.Шестаков), факторно-диапазонного анализа (И.К.Гавич); суть их заключается в экспериментальной (обычно на модели) оценке влияния того или иного элемента фильтрационной схемы на конечный результат прогнозного расчета.

• ГРАНИЧНЫЕ УСЛОВИЯ потока в плане и в разрезе (ГУ). Они должны быть определены для области ожидаемой воронки депрессии. Но существует и обратная связь - размер воронки, в свою очередь, зависит от характера и положения граничных условий, поэтому вопрос о необходимых размерах области решения прогнозной задачи приходится решать путем последовательных приближений.
ГУ могут быть внешними и внутренними; внешние должны быть определены в любом случае, внутренние - если они имеются.
Для каждого граничного элемента необходимо обосновать:

• пространственное положение и форму граничного условия (точка, линия, поверхность),
• гидродинамический род условия,
• количественные показатели условия (для каждого рода - свой набор).

Возможные варианты РОДА ГРАНИЧНЫХ УСЛОВИЙ: обычно говорят о трех родах граничных условий, хотя можно обойтись и двумя.
Математическое описание граничных условий делаем (для простоты) в удельной форме, т.е. на единицу (длины, площади) граничного элемента.

= Граничное условие 2 рода - ЗАДАННОЙ ЯВЛЯЕТСЯ ФУНКЦИЯ РАСХОДА ЧЕРЕЗ ГРАНИЦУ: 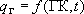; здесь ГК - набор координат граничного элемента, т.е. 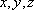в зависимости от мерности потока и границы.
Что значит "является заданной"?
Это значит, что функциональное описание величины трансграничного расхода известно заранее на весь период прогноза и не зависит от изменений, происходящих в области под влиянием водозабора в прогнозный период. Напор на границе 2 рода на прогноз неизвестен и вычисляется как результат решения.
Пример: поток, приходящий в расчетную область из удаленных областей питания ("боковой приток"); его величина не зависит ни от каких изменений напора 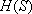в расчетной области, т.е. не реагирует на работу водозабора.
Частные случаи ГУ 2 рода:

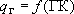- - расход через границу не зависит от времени, но может быть разным на разных участках границы;
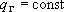- - расход через границу не зависит от времени и одинаковый для всей границы;
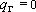- - непроницаемая граница.

= Граничное условие 3 рода-ЗАДАННЫМ ЯВЛЯЕТСЯ ЛИНЕЙНЫЙ ХАРАКТЕР СВЯЗИ МЕЖДУ РАСХОДОМ ЧЕРЕЗ ГРАНИЦУ И НАПОРОМ В ПЛАСТЕ (точнее - перепадом напоров между пластом и границей).
На такой границе неизвестны ни напор 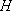в приграничной области пласта, ни трансграничный расход 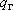; они взаимно регулируют друг друга: изменение напора (в нашем случае - понижение от действия водоотбора) вызывает пропорциональное изменение расхода, который, в свою очередь, влияет на положение уровней:

,

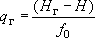при этом (рис. 3.1):

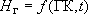, т.е. напор на границе известен заранее и не зависит от ситуации в пласте (это упрощенное описание, но пока будем рассматривать именно так);
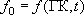- формально коэффициент пропорциональности между разностью напоров и расходом через границу; физически - это фильтрационное сопротивление границы, т.е. параметр граничного условия 3 рода. В простом случае 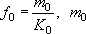- мощность слоя отложений, создающих сопротивление между граничным напором и пластом (это может быть экран под руслом реки или разделяющий слой в пластовой водоносной системе), 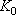- коэффициент фильтрации этих отложений.

Частные случаи ГУ 3 рода:

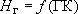- - напор на границе неизменен во времени;
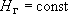- - и к тому же постоянен для всего граничного элемента;
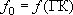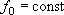- , - то же для сопротивления граничного элемента;

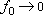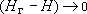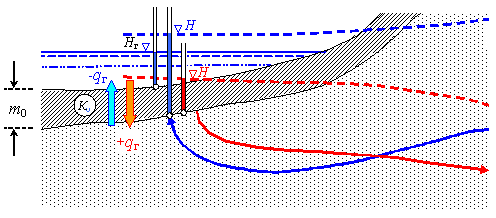
= Особая ситуация при - понятно, что в этом случае должно быть , т.е. на такой границе устанавливается условие 1 рода( ).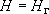

Рис.3.1. Граничное условие 3 рода на контуре водотока (водоема) в ЕСТЕСТВЕННЫХ УСЛОВИЯХ (синий цвет) и при РАБОТЕ ВОДОЗАБОРА (красный цвет)

• Завершающий пункт схематизации - распределение ИСТОЧНИКОВ-СТОКОВ. Сюда относят:

• все виды поступления воды в пласт (источники, балансовый знак +)
• все виды расходования воды из пласта (стоки, балансовый знак -),

которые почему-либо не вошли в вышеописанные "стандартные" ГУ.
Например, инфильтрация - это, по сути, площадное условие 2 рода с заданной интенсивностью (модулем) 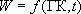- расход питания на 1 кв.м площади.
Другой распространенный пример: скважины - нагнетательные, водозаборные, дренажные и т.п. - это практически точечные (с радиусом 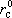) граничные условия 1 рода, если в скважинах задан уровень/понижение, а вычисляется их дебит, или 2 рода (если задан дебит, а нужно вычислить уровень/понижение в скважинах).

К вопросам расчетной схематизации относится и одна из важнейших и распространенных особенностей решения задач оценки ЭЗ - применение СУПЕРПОЗИЦИИ(СЛОЖЕНИЕ РЕШЕНИЙ). Этот прием, разумеется, является общим для всех задач фильтрации и должен быть уже в принципе рассмотрен в курсе "Гидрогеодинамика".
Его математическое содержание - согласно теореме наложения, линейное дифференциальное уравнение можно разложить на два уравнения, решить каждое отдельно, полученные решения сложить - их сумма будет являться решением общего исходного уравнения. Как это свойство используется при решении задач расчета водозаборных сооружений ?
На примере планового потока (хотя вообще-то мерность неважна):

(0)

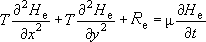
- это распределение 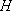в плане по 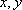и во времени в естественных условиях (без водоотбора) под действием режимообразующих факторов .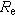
При работе водозабора :

(1)

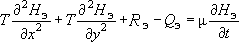
- это распределение 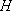в плане по 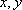и во времени под действием как-то изменившихся (в результате водоотбора с дебитом 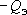) режимообразующих факторов .
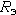Согласно принципу суперпозиции, эти уравнения можно алгебраически складывать. Из (0) вычтем (1):

(2)

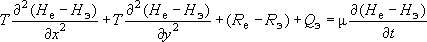
- это распределение изменений 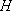в плане по 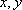и во времени под действием изменений режимообразующих факторов 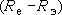и при дебите водоотбора .

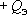Обозначим 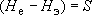, 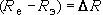; тогда (2) примет вполне понятный вид:

(2а)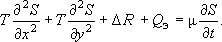

Так как нас в конечном счете, в основном, интересуют только понижения (чтобы сравнивать их с допустимыми), то можно ограничиться только решением уравнения (2а). Если же для каких-то целей необходимо распределение "полных" напоров 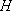, то можно прямо сложить полученные понижения (2а) с естественными напорами (0) и рассматривать их сумму как решение уравнения (1). В частности, такая необходимость возникает, если есть нужда в последующем моделировании миграции - для этого ведь нужны "полные" скорости потока.
Логичный вопрос: зачем так делать?
Упрощение фильтрационной схемы! Обычно можно считать (но доказательно!), что развитие депрессии не приведет к изменению естественных режимообразующих факторов. Тогда в уравнениях (2) или (2а) 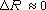и в них остаются только параметры пласта и отсутствуют режимообразующие факторы, оценка которых при разведке - вещь весьма сложная и не всегда достижимая в нужном объеме и с нужной степенью достоверности.
• Важно: при применении суперпозиции должны быть соответственно трансформированы и граничные условия - если уравнение решается относительно понижений (изменений!), то и ГУ должны быть выражены в изменениях.

- Условия 2 рода приобретают вид: 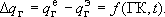При этом: если условия формирования 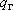при эксплуатации не изменяются, то 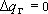, т.е. граница 2 рода в этом случае вырождается в непроницаемую! (и даже не нужно знать ).
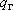- Условия 3 рода:

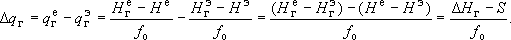
Очевидно, что если эксплуатация не вызывает изменений в поведении и величине 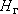, то 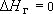и условие 3 рода упрощается до вида: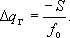

Два попутных обстоятельства:

а) Изменились балансовые знаки расходов - дебит водозабора стал положительным (см. формулу 2а), а приток в пласт через границу 3 рода стал отрицательным (ведь 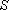положительное!).
б) Почему может возникнуть изменение 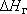? В наиболее распространенном случае условия 3 рода (на экранированной реке) такую возможность следует учитывать, если за счет инверсии разгрузки и формирования привлекаемых ресурсов расход реки существенно уменьшается, что повлечет за собой и заметное изменение глубины реки (т.е. уровня реки).

Итак, общее правило: при решении в понижениях (ур. 2а) на границах учитываются только изменения, возникшие под влиянием эксплуатационных изменений напора в пласте.
То же относится и к источникам-стокам:

- если 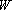не зависит от 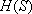, то 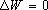, т.е. неизменная инфильтрация при решении в понижениях "исчезает" из решения, что крайне заманчиво, так как ее (и уж тем более ее распределение по площади месторождения) мы обычно знаем очень неточно;
- для водозаборной скважины "изменением" является ее дебит 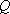, так как его не было в естественных условиях.

Теперь вернемся собственно к ГИДРОДИНАМИЧЕСКОМУ МЕТОДУрасчетов водозаборных сооружений.

АНАЛИТИЧЕСКИЕ РАСЧЕТЫ, т.е. применение формул теории притока к скважинам - применяются очень часто, особенно для небольших водозаборов с простой расчетной схемой и небольшой областью влияния. Для использования аналитических решений вынужденно и довольно значительно упрощаются реальные условия.Неизбежные требования к расчетной схеме:

1) режим во времени - не всегда есть решения для нестационарного режима,
2) пространственная структура - как правило, одномерная (радиальная или линейная); уже для плановой структуры практически нет решений,
3) пласт однородный, в лучшем случае - одна граница неоднородности,
4) границы правильной формы (прямая линия, угол, окружность) и однородны по количественным характеристикам,
5) водозабор - одиночная скважина; для нескольких скважин расчет возможен, но заметно усложняется.

Из-за необходимости таких упрощений возникают два неприятных момента:

- есть опасность, что будут неосознанно "потеряны" какие-то важные элементы расчетной схемы,
- упрощения всегда делаются в сторону "ужесточения" схемы, следовательно, занижаются реальные эксплуатационные возможности месторождений.

Достаточно часто приходится иметь дело с СИСТЕМАМИ СКВАЖИН.

- контурные - скважины в плане расположены по правильному контуру (прямая линия, кольцо...);
- площадные - скважины расположены в пределах некоторой площади.

Другой принцип классифицирования:

- упорядоченные - существует закономерность во взаимоположении скважин;
- неупорядоченные - скважины расположены произвольно.

Легко сообразить, что основной сложностью при расчете систем водозаборных скважин является необходимость учета их ВЗАИМОДЕЙСТВИЯмежду собой; в принципе возможно также взаимовлияние соседних водозаборных участков и даже соседних водозаборов. В результате могут возникать громоздкие расчеты.
Достаточным и абсолютно точным является расчет взаимодействия скважин по принципу "сложения решений": понижение в каждой скважине системы есть сумма "собственного" понижения и понижений от действия всех остальных скважин системы:

,

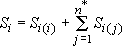где - общее количество взаимодействующих скважин, знак * означает, что из суммирования должен быть исключен член с номером ;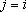
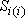- "собственное" понижение в 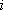-ой скважине под действием дебита 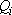на расстоянии ;
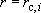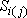- понижение в 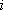-ой скважине от действия 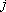-ой скважины с дебитом 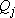на расстоянии .

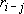Для демонстрации идеи гидродинамического метода расчета водозабора рассмотрим условный, предельно упрощенный пример на основе известных студентам материалов Звенигородской учебной практики.
Предположим, что местная администрация решила создать единую, централизованную систему водоснабжения сел Каринское, Волково, Луцино, домов отдыха, пансионатов, детских лагерей и т.д. - с суммарной заявленной потребностью 8 тыс. куб.м/сут (примерно на 15-20 тыс.человек).
Нужно решить (обосновать!) как минимум такие вопросы:

- Перспективный водоносный горизонт ?
- Наиболее благоприятное место расположения водозабора ?
- Наиболее экономичная конструкция и схема водозабора ?

1) Водоносный горизонт - вероятно, 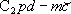: высокие фильтрационные свойства, хорошее качество воды, неглубокое залегание. В то же время этот горизонт относительно слабо защищен от поверхностных загрязнений (хотя и лучше, чем подземные воды в аллювии р.Москвы). Поэтому при реальных работах следовало бы изучить вопрос о возможности использования более глубоких горизонтов в 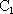: посмотреть имеющиеся материалы предшествующих исследований, пробурить одну-две глубокие скважины...
2) Место - как мы уже говорили, здесь может сталкиваться масса условий, часто противоречивых. Однако, будем считать, что все вопросы, связанные с размещением водозабора, так или иначе решены и выбрано место - поверхность I надпойменной террасы в районе учебного опытного куста (сравнивать не с чем, так как по площади материалов у нас нет).
3) Конструкция и схема водозабора - очевидно, что следует стремиться к наиболее дешевому варианту водозахватного сооружения (минимальное количество скважин, минимальная их глубина, компактное взаиморасположение). Несомненно, что нужно использовать вертикальные скважины, причем достаточна их глубина порядка 30-35 м (учитывая данные расходометрических испытаний в интервале известняков).
Схема водозабора (количество и взаиморасположение скважин) - определяется путем решения нескольких вариантов гидрогеодинамического расчета. Для этого предварительно необходимо обосновать расчетную фильтрационную схему, используя хотя бы тот минимум данных, которые получены в ходе практики.

а) ожидаемый режим фильтрации во времени при работе водозабора - судя по опытным данным, при снижении уровней в водоносном горизонте известняков достаточно быстро развивается перетекание из аллювия и затем - приток из реки в аллювий, что создает стационарную балансово-гидродинамическую ситуацию, которую можно прогнозировать на неограниченно долгое время. 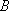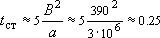Подтвердим это расчетом возможного времени стабилизации в условиях перетекания, приняв (по данным интерпретации кустовой откачки из скв.1) фактор перетекания = 390 м и пьезопроводность субнапорного водоносного горизонта в известняках = 3×10⁶ кв.м/сут:

сут.

Полученная оценка (около 6 часов) близко совпадает с фактически наблюдающимся временем стабилизации при проведении учебных опытных откачек.
б) пространственная структуратечения при работе водозабора - в целом, трехмерная: плоско-плановое течение в пласте известняков и в аллювии и вертикальный приток из аллювия через слабопроницаемый глинистый слой. Однако, чтобы не усложнять расчет, можно задавать приток из аллювия с помощью площадного граничного условия 3 рода на кровле пласта известняков; тогда можно рассматривать только двумерное плоско-плановое течение в известняках.
в) распределение параметров по площади - таких сведений у нас практически нет, поэтому вынужденно считаем область однородной по всем параметрам. Поскольку расчет будет выполняться для стационарного режима, то единственным необходимым параметром является проводимость пласта известняков 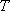= 800 кв.м/сут.
г) граничные условия(тоже не очень уверенно, так как имеем данные только по одной точке опробования):
- в плане водоносная система неограниченная (во всяком случае, для относительно небольшой области влияния откачки);
- снизу (в подошве): непроницаемая граница по подстилающим глинам ( ? );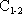
- сверху (в кровле): площадное условие 3-го рода по подошве слабопроницаемого слоя между аллювием и известняками, фактор перетекания порядка 390 м; уровень в аллювии при откачке снижался незначительно и в локальной области, поэтому можно принять .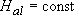
д) скважины водозабора -совершенные, так как вскрывают основную проводящую зону в разрезе пласта известняков; диаметр фильтровой части водозаборных скважин можно принять 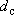= 400 мм ( 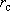= 0.2 м ).

Для расчета водозабора используем аналитическое решение из теории скважин, соответствующее принятой расчетной схеме - неограниченный в плане пласт, с площадным перетеканием при постоянном уровне в смежном горизонте, при стационарном режиме фильтрации:

,

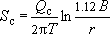(эта формула действует при 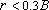, но с некоторой погрешностью ее можно использовать и в более широком диапазоне радиальных координат).
Сколько нужно скважин? Для этого сначала нужно определить максимально возможную производительность одиночной скважины (т.е. без влияния других скважин водозабора):

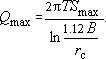
Что такое 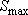? Это максимально допустимое (по гидрогеодинамическим и техническим соображениям) понижение в водозаборной скважине. При его оценке следует учитывать:

- с технической стороны: высота подъема воды для современных погружных насосов - до 100 м (можно и глубже, но дорого!),
- с гидрогеодинамической точки зрения:нежелательно понижать уровень в пласт известняков, так как будет резко уменьшаться его проводимость (основные проводящие зоны, по данным расходометрии, расположены именно в верхней части пласта).

Наиболее простое решение - принять допустимое понижение до кровли известняков, т.е. округленно 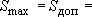6 м.

Тогда 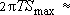3.16×10⁴ куб.м/сут; 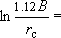7.69.
Максимально возможный дебит одиночной скважины составит 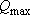≈ 4 тыс. куб.м/сут. Следовательно, сколько скважин нужно для получения заявленной потребности? Казалось бы, две равнодебитных. Но на каком расстоянии 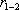их расположить?
Выведем расчетную формулу для понижения в любой из этих двух скважин (понятно, что в неограниченной однородной области понижения в них будут одинаковыми, поскольку равны дебиты 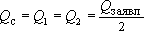). По принципу сложения решений:

_,

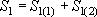где 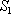- полное понижение в скв.1, 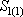- "собственное" понижение в скв.1, 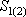- понижение в скв.1 от действия скв.2.
Соответственно:

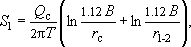
откуда можно оценить дебит, с которым может работать каждая скважина при допустимом понижении:

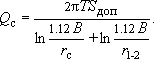
Далее для наглядности будем действовать простым подбором, хотя это уравнение решается относительно 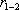достаточно просто. Для первого приближения примем, например, 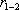= 10 м. Тогда 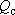= 3.16×10⁴ / (7.69 + 3.78) = 2.76 тыс. куб.м/сут, т.е. две скважины в сумме дадут только 5.5 тыс. куб.м/сут !
Что делать? Конечно же, "раздвигать" скважины. Примем 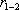= 50 м: 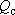= 3.16×10⁴ / (7.69 + 2.17) = 3.2 тыс. куб.м/сут. Мало!
Разводим скважины еще дальше 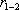= 100 м: 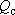= 3.16× 10⁴ / (7.69 +1.47) = 3.45 тыс. куб.м/сут. Все равно мало!
Придется сообразить, что двумя скважинами можно получить заявленный дебит 8 тыс. куб.м/сут только в том случае, если они не будут взаимодействовать между собой, т.е. если 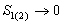, что достижимо только, если 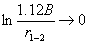. Это, в свою очередь, возможно только, если 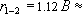440 м.
Итак, первый, самый простой вариант водозабора: две скважины на расстоянии 440 м (не менее) друг от друга.
Чтобы сделать водозабор компактнее, придется увеличивать количество скважин. Поэтому следующий вариант расчета - три равнодебитные скважины с дебитами 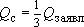= 2.67 тыс. куб.м/сут; для них самая компактная схема расположения - в вершинах равностороннего треугольника, т.е. 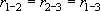= (рис. 3.2, а).
Рассуждая как в предыдущем случае, получим для трех скважин:

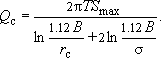
В этом уравнении только одно неизвестное - расстояние между скважинами; решение его дает ≈ 70 м. Как видно, этот вариант расстановки уже существенно компактней.
Ясно, что далее можно рассмотреть четыре скважины - в вершинах квадрата со стороной (рис. 3.2, б) при дебите каждой скважины 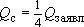= 2 тыс.куб.м/сут и т.д. (рекомендуем студентам проделать это самостоятельно).

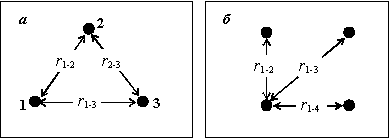
Рис. 3.2. Варианты возможной схемы водозабора

Важен общий вывод: в конкретном случае не существует некоей однозначно "правильной" схемы водозабора, можно предложить целую серию различных вариантов - либо много близкорасположенныхскважин, либо мало, но достаточно удаленных. Каждый из этих вариантов имеет свои достоинства и недостатки; оптимальный вариант всегда выбирается с учетом некоторых дополнительных, "внешних" соображений - экономических, условий строительства, землепользования и т.п. Заметим также, что на возможную величину дебита эксплуатационной скважины накладываются также ограничения, связанные с характеристиками серийных насосов и фильтрового оборудования, допустимыми скоростями потока в прискважинной зоне и др.

Завершим рассмотрение этого примера анализом источников формирования эксплуатационного водоотбора. В связи с быстрым наступлением стационара и небольшим размером депрессионной воронки (радиус питания, как мы можем судить по величине фактора перетекания, не превышает 400-500 м) можно исключить из анализа явно второстепенную и кратковременно проявляющуюся величину упругих естественных запасов основного, подольско-мячковского горизонта.
В естественных условиях по всей площади днища долины (пойменные и надпойменные террасы) происходит разгрузка потока из основного горизонта восходящим перетеканием в аллювиальный водоносный горизонт (рис. 3.3); естественная разность напоров в этих горизонтах составляет 0.5 - 1.5 м.

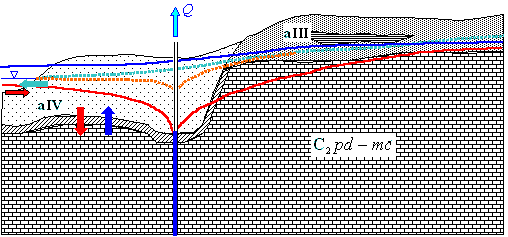
Рис. 3.3. Принципиальная балансово-гидродинамическая схема

При эксплуатационном понижении напоров основного горизонта практически по всей площади воронки интенсивность разгрузки уменьшается, а в центральной части депрессии прекращается полностью. Суммарное сокращение расхода естественной разгрузки характеризует долю использования естественных ресурсов основного горизонта.
В зоне полной инверсии разгрузки на некоторой площади возникнет перетекание обратного направления - из аллювия в основной горизонт, что означает появление в балансовой структуреводоотбора привлекаемых ресурсов для основного горизонта.
Однако, обязательно нужно задуматься и понять: в аллювиальном горизонте тоже нарушились естественные балансовые условия (хотя из него и нет водоотбора).

- Во-первых, сократилось ранее существовавшее питание аллювия в виде перетекания из известняков; уже один этот факт немин