Вопрос 2. Числовые характеристики рядов данных

Наши данные обладают уникальными числовыми характеристиками. Давайте определим некоторые из них.

Разность между максимальной и минимальной вариантой называют размахом измерения.

На наших графиках - это область определения (разность крайнего правого значения и крайнего левого значения на оси абсцисс). В нашем примере размах равен 13−1=12.
Варианты, которые встречаются чаще других, называется модой. В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем наибольшее число, и смотрим, какому варианту оно соответствует. На графике, это точка в которой достигается максимальное значение. Наиболее важная характеристика – среднее значение (среднее арифметическое или просто среднее).
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
(1∗9+2∗3+3∗4+4∗3+5∗2+6∗2+7∗2+8∗2+9∗2+10∗4+11∗2+12∗2+13∗3) /40=5,775
Пример.
На экзамене по математике 25 обучающихся первого курса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в ряде – варианты измерений.

Составим сгруппированный ряд: 2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:

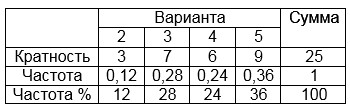
в) Нарисуем графики:
Полигон распределения данных:

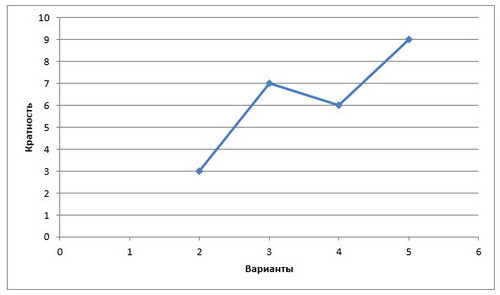
Полигон распределения частот:

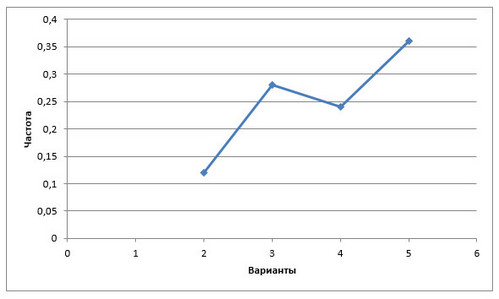
Полигон распределения частот процентов:

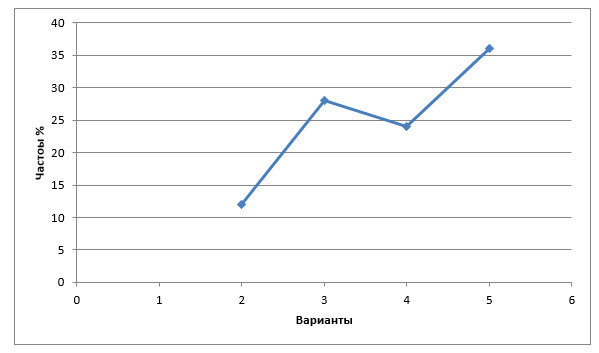
Все графики похожи между собой, различия только в масштабе оси ординат.
г) Найдем среднее значение:
2∗0,12+3∗0,28+4∗0,24+5∗0,36=0,24+0,84+0,96+1,8=3,81

Мода: чаще всего встречается оценка пять, она и будет модой.
Размах: 5−2=3.