Исследование работы последовательного RLC контура при изменении его параметров и частоты
Добротность (резонанс напряжений)
Отношение реактивного сопротивления хL или хс к активному называется добротностью резонансного контура.
Qg= 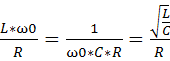 ; тогда UL=UC=E* Qg
; тогда UL=UC=E* Qg
Добротность показывает во сколько раз напряжение на индуктивности или ёмкости превышает напряжение на входе схемы в резонансном режиме .
На практике в радиотехнических устройствах Qg может доходить до 300 и даже больше.
Построим векторную диаграмму для режима резонанса.
UL UC UL
ИЛИ
UC UR=E I
UR=E I
Характеристическим сопротивлением Р называют отношением напряжения на L и С в режиме резонанса к току.
Р= Qg*R=ω0*L= 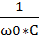 =
= 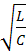
Исследование работы последовательного RLC контура при изменении его параметров и частоты
Пусть параметры контура RLC и величина ЭДС постоянны, но меняется частота ω. Определим характер изменения тока I и напряжений UL и UC как функции от ω.
Ток в цепи определим по формуле :
I= 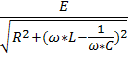
При изменении 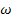 меняется реактивное сопротивление цепи
меняется реактивное сопротивление цепи 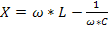 :
:
При ω→0 сопротивление Х→-∞ и ток I→0;
Найдём напряжение на индуктивности и ёмкости
UL=I*ω*L= 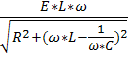
UC=I* 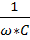 =
= 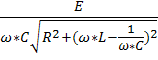
При ω→0 UL→0 Uс=Е
При ω→ 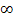 UL→Е Uс→0
UL→Е Uс→0
Построим график зависимости I,UL,UC от ω
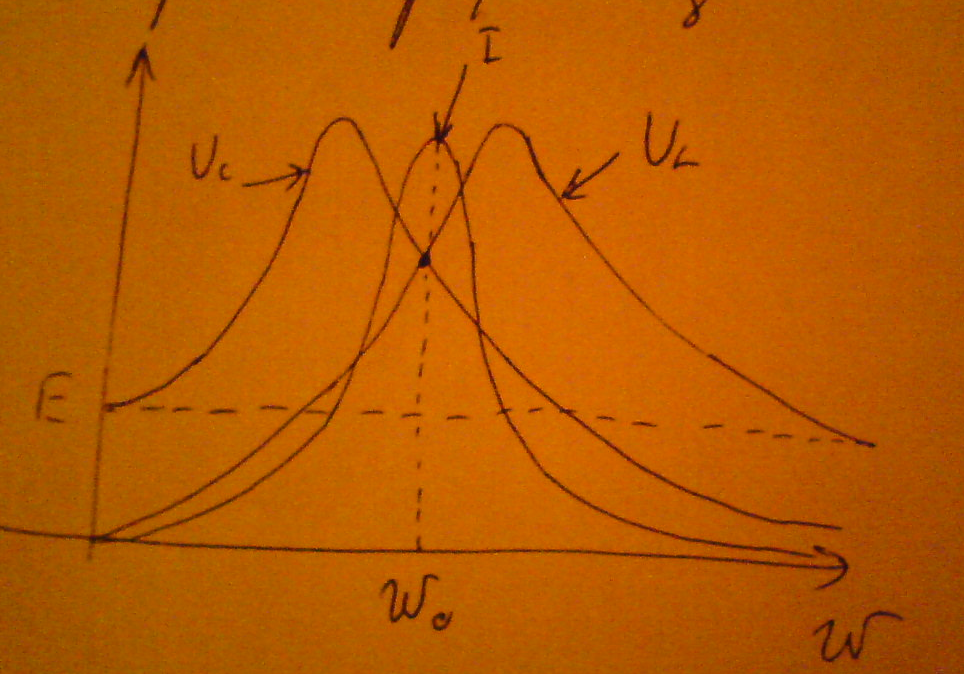
Из рисунка видно ,что максимумы напряжений на индуктивности UL и ёмкости UC имеют место при частотах ,не равных резонансной частоте ω0= 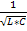
Построим график зависимости I от ω для различных значений R при неизменных L, C и E.
Чем меньше сопротивление ,тем больше добротность и больше значение тока при резонансе.
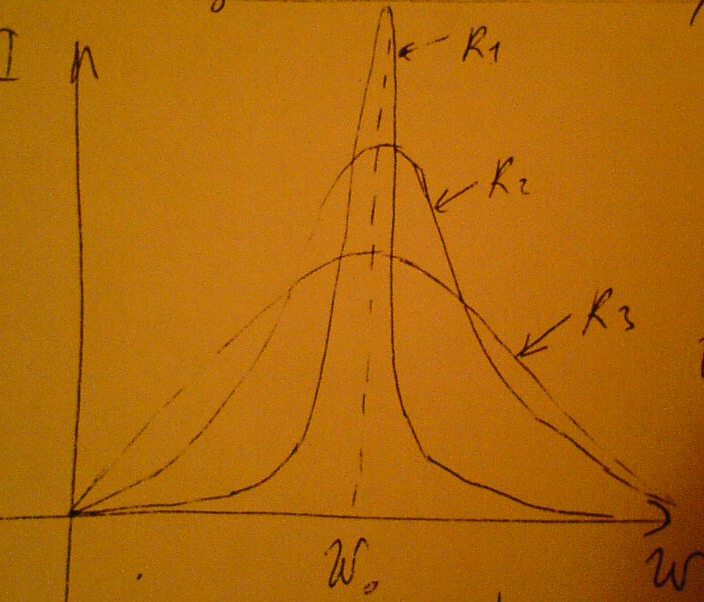 рис а).
рис а). 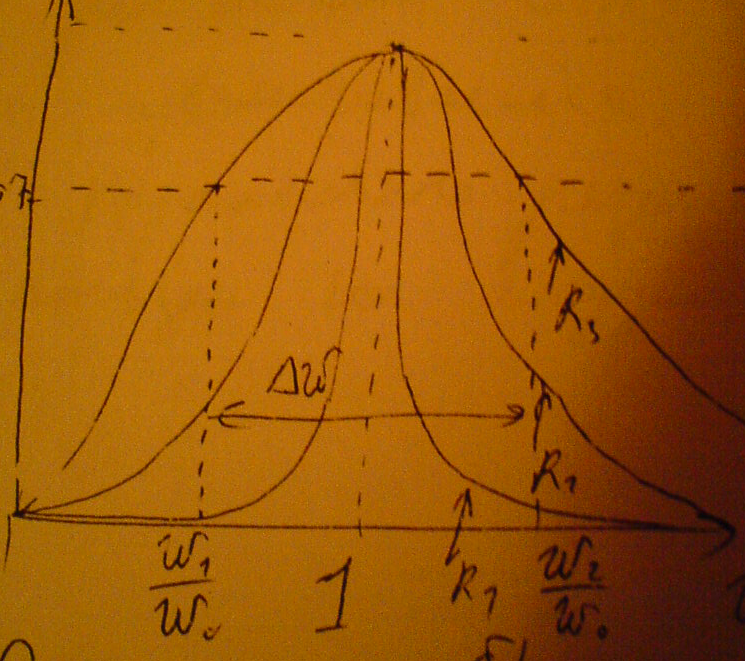 рис б)
рис б)
При этом Q1>Q2>Q3
I0
Обычно кривые изображают в относительных единицах (в нормальном виде) откладывая ток в долях от тока при резонансе ,а частоту -в долях от резонансной частоты(рис б).
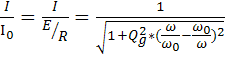
Особое значение приобретает полоса частот при которых величина тока превышает значение 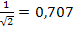 от максимального тока при резонансе .
от максимального тока при резонансе .
Эта полоса частот называется полосой пропускания .Полоса пропускания ∆ω=ω2-ω1 зависит от зависит от добротности контура .зная полосу пропускания и резонансную частоту можно определить добротность :
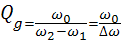
Таким образом ,чем меньше полоса пропускания ,тем выше добротность контура.
Построим векторные диаграммы для 3 случаев:
1 ω<ω0 2 ω=ω0 3 ω>ω0
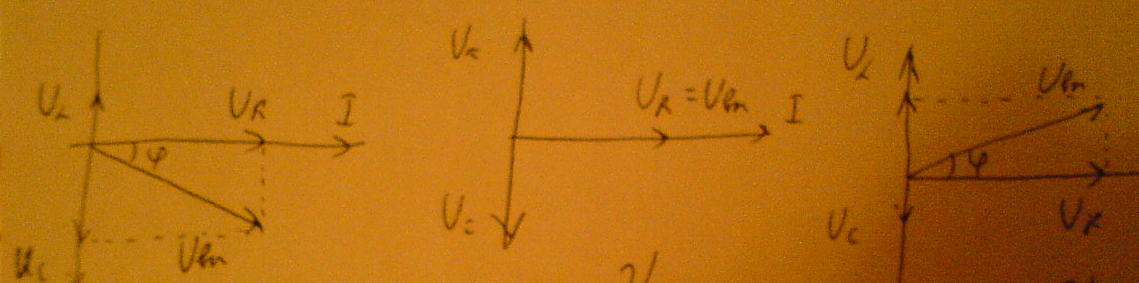
1)при частоте ниже резонансной сопротивление контура носит ёмкостной характер ,напряжение отстаёт по фазе от тока ,реактивная составляющая полного сопротивления имеет отрицательный знак .
2)на резонансной частоте сопротивление чисто активное ,напряжение совпадает с током по фазе, реактивная составляющая сопротивления равна 0
3)при частоте выше резонансной сопротивление контура носит индуктивный характер , напряжения опережает ток по фазе ,реактивная составляющая полного сопротивления имеет положительный знак.
На рис * показан график зависимости реактивной составляющей полного сопротивления от частоты X=XL-Xc= 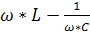

| <== предыдущая лекция | | | следующая лекция ==> |
| Измерение активной мощности с помощью электродинамического ваттметра | | | Частотная характеристика сложного двухполюсника. |
Дата добавления: 2016-05-28; просмотров: 3330;











