Преобразователи кодов, шифраторы, дешифраторы
В цифровых системах используется множество арифметических кодов. Выбор кода влияет на удобство взаимодействия с устройствами ввода-вывода, на простоту выполнения арифметических операций, на аппаратные затраты и надежность. Преобразователи кодов могут быть синтезированы как комбинационные схемы. В устройствах, использующих декадную форму отображения информации (цифровые измерительные приборы, калькуляторы и др.) широко используется двоично-десятичный код 8421 (код образуется путем представления каждой десятичной цифры двоичным кодом).
Рассмотрим синтез преобразователя кода 8421 в код Грея. Функционирование преобразователя представлено таблицей истинности (см. табл. 4.1), которой соответствуют карты Карно (см. рис. 4.1). На картах отмечены избыточные комбинации (Ф), соответствующие десятичным цифрам от 10 до 15. Из карт Карно после доопределения получим выражения для функций выхода преобразователя в СДНФ:
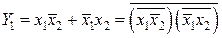 ;
;
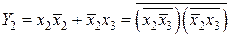 ;
;
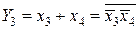 ;
;
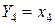 .
.
Таблица 4.1
| Десятичное число | Код 8421 | Код Грея | ||||||
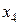
| 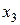
| 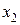
| 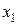
| Y4 | Y3 | Y2 | Y1 | |
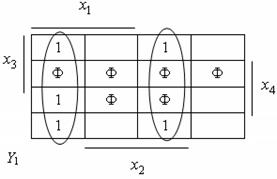
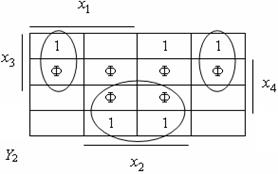
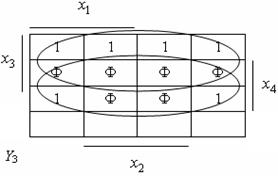
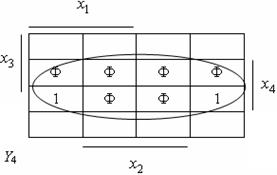
Рис. 4.1. Карты Карно преобразователя кодов
Схема, выполненная на основании этих структурных формул в базисе И-НЕ, приведена на рис. 4.2.


Рис. 4.2. Структурная схема преобразователя кодов
 Шифраторы – преобразователи позиционного кода в двоичный, т. е. преобразующие сигнал 1 на одном из входов в соответствующий код на выходных шинах. Если на выходе снимается m – разрядный код, то максимальное число входов n = 2m. Если используются все 2m входы, то такой шифратор называют полным, если не все, – то неполным. Функционирование шифратора 4
Шифраторы – преобразователи позиционного кода в двоичный, т. е. преобразующие сигнал 1 на одном из входов в соответствующий код на выходных шинах. Если на выходе снимается m – разрядный код, то максимальное число входов n = 2m. Если используются все 2m входы, то такой шифратор называют полным, если не все, – то неполным. Функционирование шифратора 4 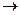 2 представлено таблицей истинности (табл. 4.2). Из таблицы следует:
2 представлено таблицей истинности (табл. 4.2). Из таблицы следует:
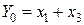 ;
;
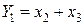 ,
,
т. е. для построения такого шифратора требуется два ЛЭ ИЛИ на два входа.
Аналогично строятся шифраторы на большее число разрядов.
Недостаток таких шифраторов – неоднозначность, если возбуждены сразу несколько входов. Чтобы шифратор откликался только на один возбужденный вход, строят приоритетные шифраторы. В них, в случае одновременного возбуждения нескольких входов, выходной код будет соответствовать «старшему» («младшему») номеру из возбужденных входов. На рис. 4.3 приведено обозначение такого шифратора. Приоритетный шифратор имеет дополнительные выводы: Е1 – сигнал включения шифратора, Е0 – сигнал об отсутствии возбужденных входов, G – сигнал на выходе, свидетельствующий о наличии хотя бы одного возбужденного входа.
 Наличие выводов Е1, Е0, G позволяет наращивать разрядность шифраторов.
Наличие выводов Е1, Е0, G позволяет наращивать разрядность шифраторов.
Дешифратор – преобразователь двоичного n-разрядного кода в унитарный 2n-разрядный код, т. е. дешифратор имеет n входов и m = 2n выходов. Каждому набору входных переменных соответствует возбуждение (появление логической единицы или нуля) на выходе, десятичный номер которого соответствует двоичному коду.
 Рассмотрим пример построения двухразрядного дешифратора. Функционирование дешифратора можно представить таблицей истинности (табл. 4.3) Из таблицы получим выражения для функций выхода (Y1) дешифратора:
Рассмотрим пример построения двухразрядного дешифратора. Функционирование дешифратора можно представить таблицей истинности (табл. 4.3) Из таблицы получим выражения для функций выхода (Y1) дешифратора:
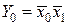 ;
;
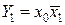 ;
;
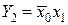 ;
;
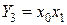 .
.
Из полученных соотношений видно, что для построения дешифратора нужно четыре логических элемента И на два входа и два инвертора. Часто дешифраторы строятся в базисе И-НЕ (см. рис. 4.4). В этом случае выходы будут инверсными, т. е. возбужденному выходу соответствует логический ноль; и чтобы получить прямой выход, надо еще четыре инвертора. Для расширения возможностей дешифратора в интегральных схемах делается еще один вход Е – разрешение. Для его организации берутся элементы И-НЕ на 3 входа – третьи входы объединятся и образуют вход разрешения. В этом случае дешифратор работает, когда на входе Е логическая единица.
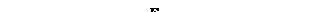

Рис. 4.4. Структура дешифратора
 Графическое изображение дешифраторов приведено на рис. 4.5. Если выходы инверсные, то обозначаются кружочками.
Графическое изображение дешифраторов приведено на рис. 4.5. Если выходы инверсные, то обозначаются кружочками.
Наличие входа разрешения позволяет наращивать разрядность дешифратора. На рис. 4.6 показано, как построить трехразрядный дешифратор, используя двухразрядные.


Рис. 4.6. Наращивание дешифраторов
Для всех наборов входных переменных, где x3 = 0, будет работать DC2, т. к. на его вход Е2 будет приходить единица. Когда x3=1, соответственно работает дешифратор DC3. Таким образом, получается три входа и восемь выходов. Для расширения числа входов и выходов можно воспользоваться параллельным (прямоугольным) дешифратором, но для этого, кроме дешифраторов, нужны элементы 2И.
Используя дешифраторы и дополнительные логические элементы, можно реализовать практически любую логическую функцию.
Рассмотрим такой пример
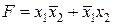 .
.
Таблица истинности для этой функции имеет вид табл. 4.4. Для ее реализации необходим дешифратор 2 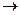 4 и логический элемент ИЛИ на два входа (рис. 4.7). Когда x1или x2 равны единице (для набора n = 1 и n = 2), на выходах дешифратора (1 или 2) появляется единица и соответственно выходная функция будет равна 1.
4 и логический элемент ИЛИ на два входа (рис. 4.7). Когда x1или x2 равны единице (для набора n = 1 и n = 2), на выходах дешифратора (1 или 2) появляется единица и соответственно выходная функция будет равна 1.

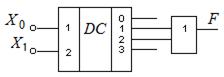
Рис. 4.7. Структурная схема сумматора
по модулю 2 на дешифраторе
Мультиплексоры
 Мультиплексор – многовходовая схема с одним выходом, осуществляет коммутацию одного из информационных входов на выход. Входы мультиплексора подразделяют на информационные (x1 … xn) и управляющие (адресные) (А1 … Аk). Обычно число информационных входов n=2k, где k – число адресных входов. Код, поступающий на адресные входы, определяет, какой из информационных входов должен быть соединен с выходом.
Мультиплексор – многовходовая схема с одним выходом, осуществляет коммутацию одного из информационных входов на выход. Входы мультиплексора подразделяют на информационные (x1 … xn) и управляющие (адресные) (А1 … Аk). Обычно число информационных входов n=2k, где k – число адресных входов. Код, поступающий на адресные входы, определяет, какой из информационных входов должен быть соединен с выходом.
Функционирование двухразрядного мультиплексора представлено таблицей истинности (табл. 4.5). Работа мультиплексора описывается логическим уравнением
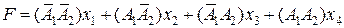 . (4.1)
. (4.1)
В соответствии с уравнением для построения мультиплексора необходим элемент 3И-4ИЛИ и два инвертора. Структурная схема приведена на рис. 4.8, графическое изображение мультиплексоров – на рис. 4.9.




| Рис. 4.7. Структурная схема мультиплексора | Рис. 4.9 Условное обозначение мультиплексоров |
Мультиплексоры в интегральном исполнении, кроме адресных и информационных входов, имеют один или два входа разрешения (Е). Наличие этих входов позволяет осуществлять наращивание мультиплексоров.
На рис. 4.10 показано построение трехразрядного мультиплексора на двух двухразрядных. В качестве третьего адресного входа (А3) используется вход разрешения (Е).


Рис. 4.10. Схема наращивания мультиплексоров
Мультиплексоры являются универсальными логическими устройствами, на основе которых можно строить различные комбинационные схемы. Возьмем двухразрядный мультиплексор (4®1). В уравнении (4.1), описывающем его работу в скобках представлены минтермы адресующих переменных. При переходе к режиму универсального логического модуля (УЛМ) меняют назначение входов мультиплексора: адресные входы становятся информационными (Аi=Xi),а информационные – настроечными. В этом случае при каждом наборе входных переменных (х) к выходу подключается соответствующий вход. Подавая на этот вход значение функции при этом наборе (0, 1), на выходе будет реализована данная функция. При увеличении числа аргументов (х) растет количество настроечных входов. Перенос одного или нескольких аргументов (х) в число сигналов настройки позволяет реализовать на том же оборудовании функцию с числом аргументов большим, чем при настройке УЛМ с константами (0 или 1). В этом случае надо использовать адресные входы для тех аргументов (входных переменных реализуемой функции), которые входят в большинство минтермов. В качестве примера рассмотрим реализацию функции 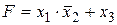 с помощью мультиплексора 4®1. Примем х1=A1; х2=A2, тогда таблица состояний для данной функции может быть представлена в виде табл. 4.6. При
с помощью мультиплексора 4®1. Примем х1=A1; х2=A2, тогда таблица состояний для данной функции может быть представлена в виде табл. 4.6. При
х1= х2 = 0 на выход будет подключен первый вход мультиплексора и на него подается аргумент х3 и т. д. (рис 4.11).
Таблица 4.6
| 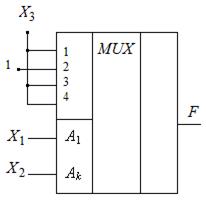 Рис. 4.11. УЛМ на мультиплексоре
Рис. 4.11. УЛМ на мультиплексоре
|
Демультиплексор – схема, выполняющая обратную функцию мультиплексора, т. е. это комбинационная схема, имеющая один информационный вход, n информационных выходов (F1¸Fn) и K управляющих входов.
Полный демультиплексор имеет n = 2K выходов (Таблица состояний демультиплексора 1®4 см. табл. 4.7).
 Согласно таблице уравнения, описывающие работу демультиплексора, имеют вид:
Согласно таблице уравнения, описывающие работу демультиплексора, имеют вид:
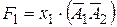 ;
;
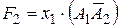 ;
;
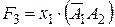 ;
;
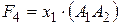 .
.
Соответственно, для построения требуется два инвертора и четыре элемента И на три входа. Условное изображение демультиплексора приведено на рис. 4.12.
 |
Рис. 4.12. Условное изображение
демультиплексора
Надо заметить, что мультиплексоры и демультиплексоры в сериях на биполярных транзисторах коммутируют только цифровые сигналы, т. е. 0 или 1.
В сериях на полевых транзисторах строятся двунаправленные ключи. На рис. 4.13 приведена функциональная схема такого мультиплексора. В зависимости от сигнала на адресном входе замыкается соответствующий ключ, через который передаются как цифровые, так и аналоговые сигналы. В зависимости от того, что использовать в качестве входных и выходных выводов, такая схема может работать и как мультиплексор, и как демультиплексор. Возможность коммутации двуполярных сигналов определяет широкое применение таких мультиплексоров в аналоговых устройствах для управления их параметрами цифровым кодом.

Рис. 4.12. Функциональная схема мультиплексора-демультиплексора
Сумматоры
Сумматором называется комбинационная схема, предназначенная для сложения двоичных чисел. Простейшая задача – сложение двух одноразрядных чисел. Для того чтобы разработать логическую схему, в первую очередь следует рассмотреть все возможные сочетания входных переменных, на основании чего можно составить таблицу состояний. При сложении одноразрядных чисел A и B могут наблюдаться следующие комбинации:
| + | = | 0; | ||
| + | = | 1; | ||
| + | = | 1; | ||
| + | = | 10, |
 т. е. если A=B=1, происходит перенос в следующий (более старший) разряд. Следовательно, такой сумматор должен иметь два выхода: один для формирования части суммы, относящейся к данному разряду, и второй – для переноса в следующий разряд. Представляя числа
т. е. если A=B=1, происходит перенос в следующий (более старший) разряд. Следовательно, такой сумматор должен иметь два выхода: один для формирования части суммы, относящейся к данному разряду, и второй – для переноса в следующий разряд. Представляя числа 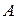 и
и 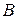 логическими переменными a0, b0, составим таблицу состояний (табл. 4.8), где S0 – сумма, P – сигнал переноса.
логическими переменными a0, b0, составим таблицу состояний (табл. 4.8), где S0 – сумма, P – сигнал переноса.
Отсюда составляем логические уравнения в СДНФ:
1) 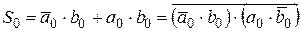 ;
;
2) P = a0× b0
и строим структурные схемы (рис. 4.14, рис. 4.15).



Рис. 4.14. Сумматор по модулю два Рис. 4.15. Схема переноса
Схема, реализующая уравнение 1, называется исключающее ИЛИ, выпускается в сериях как отдельная микросхема. Графическое обозначение приведено на рис 4.16. Логическая операция, выполняемая этой схемой, –
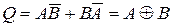 ,
,
где 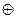 – символ суммирования по модулю два.
– символ суммирования по модулю два.
|
|
|
 Если объединить структурные схемы рис. 4.14 и рис. 4.15, то получается схема сумматора с двумя входами, такая схема называется полусумматором, условное обозначение – рис. 4.17.
Если объединить структурные схемы рис. 4.14 и рис. 4.15, то получается схема сумматора с двумя входами, такая схема называется полусумматором, условное обозначение – рис. 4.17.
|
|
|
|
Соединяя полусумматоры и полные сумматоры, получают устройства для сложения многоразрядных чисел.
|
 
| 
|
а б
Рис. 4.18. Полный сумматор:
а – структурная схема; б – условное обозначение
Дата добавления: 2016-06-22; просмотров: 4733;