Свойство д) распространяется на случай алгебраической суммы любого конечного числа функций.

Таблица основных интегралов

Интегрирование есть действие, обратное дифференцированию. Поэтому, для того чтобы проверить, правильно ли найден данный интеграл, достаточно продифференцировать найденную первообразную. Если при этом получим подынтегральную функцию, то интеграл найден верно.

Из определения интеграла следует, что всякая формула для производной конкретной функции, т.е. формула вида (1) может быть записана в виде интегральной формулы (3). Формулы интегрирования получаются обращением соответствующих формул дифференцирования. Используя это соображение и таблицу производных, составим следующую таблицу неопределенных интегралов.

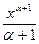1. dх = + С (a ¹-1)

В частности, при a = 0 имеем 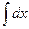= x + С

2. = ln|х| + С

3. 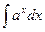= 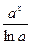+ С, а>0, а¹1

В частности,

3а. = е^х + С

4. = -

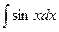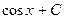
5. =

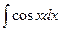6. =

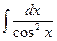
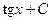
7. =

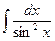8.

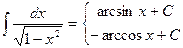
9.

Заметим, что формулы 2,6,7,8 справедливы лишь для тех значений х, при которых не происходит обращения в нуль знаменателя.

Для вывода этих формул, как уже отмечалось, используется свойство в) неопределенного интеграла, а именно, дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал -подынтегральное выражение.

Справедливость всех представленных интегралов легко проверить, если

продифференцировать их правые части.

Проверим, например, формулу 2.

Чтобы найти 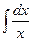, заметим, что функция 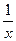непрерывна в промежутках 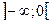и 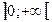, причем в каждом из них она имеет первообразную.

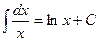В промежутке этой первообразной, очевидно, является функция lnx, т.к. , т.е при .

В промежутке 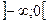первообразной по отношению к 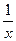является 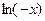, т.е.

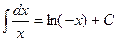при 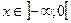. Действительно, 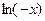существует при x<0 и .

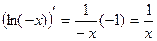Итак, оба промежутка непрерывности подынтегральной функции объединяются записью

.

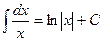Приведенные интегралы 1-9 принято называть табличными.

Лекция 2.