Кольцевой регистр сдвига единицы
Особенностью логической структуры кольцевого регистра сдвига единицы является то, что при приведении регистра к исходному состоянию один из триггеров цепочки устанавливается в единичное состояние, а остальные сбрасываются в нуль. При этом вводится прямая обратная связь между выходом последнего триггера и входом первого. Логическая структура трехразрядного кольцевого регистра сдвига единицы, выполненного на универсальных JK-триггерах, приведена на рисунке 16.10.
К исходному состоянию регистр приводится низким уровнем напряжения, подаваемым на входы начальной установки триггеров. Первый и второй триггеры приводятся к исходному нулевому состоянию, а в третий триггер записывается логическая единица. Тактирующие импульсы подаются на входы С всех триггеров одновременно.

Рисунок 16.10 – Принципиальная схема кольцевого
регистра сдвига единицы
Первый после окончания сигнала начальной установки («Пуск») тактирующий импульс переписывает единицу с выхода последнего триггера в первый. Действительно, на управлющих входах первого триггера J=1, К=0, что соответствует режиму «управление единицей». Третий триггер при этом обнуляется, т.к. на управляющий вход J подавался низкий уровень напряжения с выхода второго триггера (режим «управление нулем»). Второй триггер остается в исходном состоянии, поскольку на его входе J также был нулевой уровень. Второй тактирующий импульс сдвигает информацию на один шаг вправо и т.д. Временные диаграммы, поясняющие работу трехразрядного регистра сдвига единицы, приведены на рисунке 16.11. Нетрудно заметить, что на выходе кольцевого регистра сдвига единицы получается позиционный код без помощи дешифратора, что является его достоинством. Подобным образом можно строить пятеричные, шестеричные, восьмеричные и десятичные регистры-счетчики. Каждый из выходов приходит в активное состояние с частотой F=Fвх /n, где n – число триггеров в кольце. Следовательно, коэффициент счета численно равен числу триггеров. Для построения десятичного счетчика требуется десять триггеров (для двоичного счетчика – четыре).

Рисунок 16.11 – Временные диаграммы кольцевого регистра
сдвига единицы
Это приводит к увеличению экономических и энергетических затрат, что является основным недостатком кольцевых счетчиков. Другим недостатком кольцевого регистра является то, что любой сбой в работе (например, появление других единиц в кольце от сигнала помехи) не самоустраняется в последующем. Для устранения сбоев необходимо в цепь обратной связи включать корректирующую цепь, выполненную на простых логических элементах. К достоинствам регистра можно отнести максимальное быстродействие, определяемое только скоростью переключения применяемых триггеров. На каждом выходе сигналы имеют одинаковую задержку относительно тактирующих импульсов, равную времени задержки переключения одного триггера.
16.3.2 Кольцевой счетчик
Кольцевой счетчик, часто именуемый счетчиком Джонсона, обладает высоким быстродействием, как и кольцевой регистр, но имеет коэффициент счета Ксч = 2 n, что делает его более экономичным. Отличия в построении кольцевого счетчика от кольцевого регистра заключаются в следующем. Во-первых, все триггеры счетчика приводятся к одному нулевому состоянию. Во-вторых, обратная связь делается перекрестной: инверсный выход последнего триггера 
 соединяется с управляющим входом J первого триггера, а прямой выход Q последнего триггера подключается ко входу К первого (перекрестная обратная связь). При построении кольцевого счетчика на триггерах типа D c динамическим управлением выход
соединяется с управляющим входом J первого триггера, а прямой выход Q последнего триггера подключается ко входу К первого (перекрестная обратная связь). При построении кольцевого счетчика на триггерах типа D c динамическим управлением выход 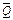 соединяется со входом D входного триггера. На рисунке 16.12 приведена схема пятиразрядного кольцевого счетчика. Перед пуском счетчик приводится к исходному состоянию путем подачи сигнала низкого уровня на входы R всех триггеров. При этом на выходе
соединяется со входом D входного триггера. На рисунке 16.12 приведена схема пятиразрядного кольцевого счетчика. Перед пуском счетчик приводится к исходному состоянию путем подачи сигнала низкого уровня на входы R всех триггеров. При этом на выходе 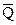 последнего триггера установится уровень лог. 1, который поступит на вход D первого триггера. После окончания сигнала начальной установки первый тактирующий импульс переведет в единичное состояние первый триггер, остальные триггеры сохранят предыдущее состояние. Второй импульс переведет в единичное состояние второй триггер, причем первый триггер сохранит предыдущее состояние. Так будет продолжаться до прихода пятого импульса (говорят, что по счетчику распространяется волна единиц). После пятого импульса ситуация изменится на обратную: на выходе
последнего триггера установится уровень лог. 1, который поступит на вход D первого триггера. После окончания сигнала начальной установки первый тактирующий импульс переведет в единичное состояние первый триггер, остальные триггеры сохранят предыдущее состояние. Второй импульс переведет в единичное состояние второй триггер, причем первый триггер сохранит предыдущее состояние. Так будет продолжаться до прихода пятого импульса (говорят, что по счетчику распространяется волна единиц). После пятого импульса ситуация изменится на обратную: на выходе  установится лог. 0. Теперь с приходом каждого тактирующего импульса по счетчику будет продвигаться волна нулей. На приведенном рисунке сигналы на прямых выходах триггеров показаны жирными линиями. Сигналы на инверсных выходах показаны пунктирными линиями.
установится лог. 0. Теперь с приходом каждого тактирующего импульса по счетчику будет продвигаться волна нулей. На приведенном рисунке сигналы на прямых выходах триггеров показаны жирными линиями. Сигналы на инверсных выходах показаны пунктирными линиями.

Рисунок 16.12 – Принципиальная схема пятиразрядного кольцевого счетчика
Достоинством кольцевого счетчика является то, что состояние 0-1 или 1-0 для двух соседних триггеров в течение одного цикла бывает только один раз за цикл независимо от длины счетчика. Это позволяет дешифрировать любое состояние счетчика с помощью простых двухвходовых логических элементов 2И либо 2ИЛИ-НЕ (на основании правила де-Моргана). Следует отметить, что на выходах дешифрирующих ячеек не возникают ложные пики, обусловленные различными величинами задержек сигналов в разных разрядах, поскольку в каждом такте только один триггер меняет свое состояние. В качестве примера на рисунке 16.13 приведена диаграмма выделенного четвертого такта 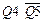 . Общий недостаток кольцевых структур заключается в том, что любой сбой (случайное включение какого-либо триггера) будет существовать сколь угодно долго, т.е. не самоустраняется. Для устранения сбоев разработаны различные варианты логических цепей коррекции обратной связи.
. Общий недостаток кольцевых структур заключается в том, что любой сбой (случайное включение какого-либо триггера) будет существовать сколь угодно долго, т.е. не самоустраняется. Для устранения сбоев разработаны различные варианты логических цепей коррекции обратной связи.
Микросхема К564ИЕ19 – пятиразрядный кольцевой счетчик (Джонсона) с предварительной установкой каждого разряда по входам S1–S5 (рисунок 16.14). Микросхема имеет информационный вход D, вход тактовый С, вход установки нуля R, входы разрешения предварительной установки каждого разряда S1–S5, вход разрешения предварительной установки ES, инверсные выходы первого – пятого разрядов (  –
– 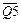 ). Логический уровень на входе разрешения предварительной установки ES высокий.
). Логический уровень на входе разрешения предварительной установки ES высокий.

Рисунок 16.13 – Временные диаграммы кольцевого счетчика
Счетчик имеет вход установки R, при подаче на который высокого уровня все разряды счетчика устанавливаются в состояние высокого уровня независимо от состояния уровня на остальных входах.
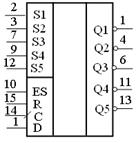
Рисунок 16.14 – Условное графическое обозначение 564ИЕ19
Упрощенная функциональная схема ИС К564ИЕ19 приведена на рисунке 16.15. По функциональной схеме можно заключить, что триггеры МСХ состоят из двух частей: одна служит для записи сигналов предварительной установки S1–S5 управляющим сигналом ES, вторая часть служит в качестве D-триггера для организации кольцевого счетчика. Выходы каждого триггера взяты с прямого плеча Q, но выведены через инверторы ( 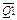 –
– 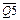 ).
).
Информационный вход D не связан ни с одним выходом триггера, что позволяет с помощью монтажных соединений получать коэффициенты деления от 2 до 10. При соединении входа D с одним из входов триггера МСХ можно получить кольцевой счетчик с четным коэффициентом деления.
В таблице 16.1 приведены способы соединения входа D с выходами  МСХ или выходом схемы элемента И, подключенной к определенным выводам ИС К564ИЕ19.
МСХ или выходом схемы элемента И, подключенной к определенным выводам ИС К564ИЕ19.
На рисунке 16.16, а показана схема включения К564ИЕ19 в режиме деления на десять. Достоинством схемы является то, что на каждом выходе формируется меандр, задержка сигнала на каждом выходе постоянна и минимальна по отношению ко входному сигналу. Диаграммы напряжений декады приведены на рисунке 16.16 б.
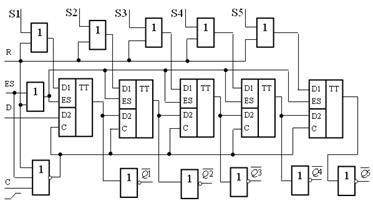
Рисунок 16.15 – Упрощенная функциональная схема К564 ИЕ19
Таблица 16.1 – Способы соединения входа D ИС К564ИЕ19
| Способ соединения выводов ИС | Соединение входа D с выходом | Соединение входа D с выходом элемента И, входы которого соединены с выходами | |||||||
| Номер вывода | 4,5 | 4,6 | 6, 11 | 11,13 | |||||
| Кдел |
Следующим достоинством описываемой декады является простота дешифрации состояния счетчика, т. е. определения числа поступивших на вход импульсов. Полный дешифратор выполняется на десяти двухвходовых логических логически ячейках И. В качестве примера на рисунке 16.17 приведена схема делителя на семь и диаграммы напряжений, позволяющие уяснить принцип его работы. Логическая схема И подключена к выводам 6, 7 ( 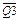 ,
,  ), а ее вывод соединен со входом D. Под воздействием сигнала R триггеры счетчика обнулены и, следовательно, на инверсных выходах
), а ее вывод соединен со входом D. Под воздействием сигнала R триггеры счетчика обнулены и, следовательно, на инверсных выходах 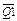 –
– 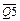 – уровни лог. 1. Логическая схема И выдает на вход D высокий уровень, который первым тактирующим импульсом запишется в первый триггер. Следующие тактирующие импульсы начнут продвигать лог. 1 вдоль по счетчику и за пять тактирующих импульсов дойдут до пятого триггера.
– уровни лог. 1. Логическая схема И выдает на вход D высокий уровень, который первым тактирующим импульсом запишется в первый триггер. Следующие тактирующие импульсы начнут продвигать лог. 1 вдоль по счетчику и за пять тактирующих импульсов дойдут до пятого триггера.
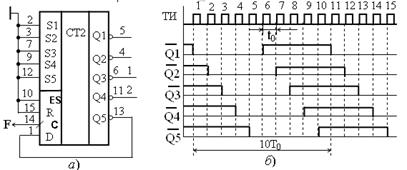
а − ИС К564ИЕ19; б − временные диаграммы
Рисунок 16.16 – Десятичная декада
При этом на инверсных выходах 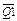 –
– 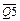 будет продвигаться волна нулей. После третьего такта на выходе схемы И установится низкое напряжение, которое четвертым тактовым импульсом запишется на Q1 (
будет продвигаться волна нулей. После третьего такта на выходе схемы И установится низкое напряжение, которое четвертым тактовым импульсом запишется на Q1 ( 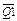 =1). Теперь в счетчике будет распространяться волна «нулей», а на
=1). Теперь в счетчике будет распространяться волна «нулей», а на  –
– 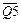 будет идти волна «единиц». Так будет продолжаться до седьмого импульса, после чего на выходе И вновь установится лог.1 и начнется новый, содержа
будет идти волна «единиц». Так будет продолжаться до седьмого импульса, после чего на выходе И вновь установится лог.1 и начнется новый, содержа
 |
щий семь периодов входной частоты.
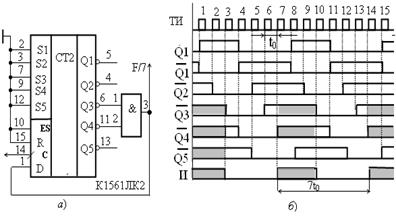
а −ИС К564ИЕ19; б − эпюры напряжений
Рисунок 16.17 – Делитель на семь
Микросхема К564ИЕ9 – четырехразрядный счетчик-делитель на восемь (кольцевой счетчик «Джонсона»). Основой кольцевого счетчика является одна перекрестная связь с выхода 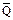 последнего триггера на вход D-первого. Важнейшим свойством счетчиков является высокое быстродействие и простота дешифратора состояний (рисунок 16.18).
последнего триггера на вход D-первого. Важнейшим свойством счетчиков является высокое быстродействие и простота дешифратора состояний (рисунок 16.18).
В качестве одного разряда в счетчике используется тактируемый MS-триггер типа D с непосредственным входом R установки нуля. Запись информации в каждый триггер осуществляется последовательно, сначала в основной – М (при отсутствии тактового импульса), затем во вспомогательный – S (по тактовому импульсу). Счетчик осуществляет счет от положительного фронта тактового сигнала С при напряжении низкого уровня на входе разрешения Е.
При высоком уровне напряжения на входе Е происходит блокировка счета. Счетчик осуществляет счет так же от отрицательного фронта сигнала Е при высоком уровне напряжения по входу С. На выходе Р формируется последовательность импульсов со скважностью Q=2 и частотой, равной Fвх/8.

Рисунок 16.18 - Условное графическое изображение ИС К564ИЕ9
Обнуление в счетчике происходит при подаче лог. 1 на вход установки нуля R, при этом выходы 0 и CR принимают состояния высокого уровня, а все остальные выходы – состояние низкого уровня. На каждом выходе дешифратора высокий уровень появляется только на период тактового импульса с соответствующим номером. Счетчик имеет выход переноса, завершает цикл счета при восьмом тактовом импульсе. Положительные фронты импульсов P используются как тактовая последовательность для последующего счетчика ИЕ9.
СЧЕТЧИКИ
Счетчик – это цифровое устройство, осуществляющее счет числа появлений на счетном входе устройства сигналов высокого или низкого логического уровня. Если уровень особо не оговаривается, то будем считать, что счетчик подсчитывает число поступивших на вход уровней лог. 1. Микрооперация счета заключается в изменении числа N в счетчике на ± 1. Счетчик, в котором выполняется микрооперация счета N = N + 1, называется суммирующим, а счетчик, реализующий микрооперацию N = N – 1 – вычитающим. Счетчик называют реверсивным, если он имеет возможность реализовать обе операции. Счетчик, образованный цепочкой из n триггеров, может однозначно подсчитать в двоичном коде N £ 2n импульсов. Число n определяет количество разрядов двоичного числа, которое может быть записано в счетчик. Число Кcч = 2n называют коэффициентом (модулем) счета. Таким образом, счетчик представляет собой логическое устройство последовательного типа, в котором новое состояние определяется предыдущим состоянием и значением логической переменной на входе.
Для представления чисел в счетчике может использоваться двоичная или двоично-десятичная системы счисления. Причем цифры двоичных разрядов числа определяются, как правило, соответствующими уровнями (лог. 0 или лог. 1) на прямых выходах триггеров. Младшие разряды счетчика относятся ко входным триггерам счетчика, а старшие – к выходным.
Основными эксплуатационными параметрами счетчика, кроме модуля счета, являются быстродействие и потребляемая мощность. Быстродействие счетчика определяется допустимой максимальной частотой входных сигналов Fmax. и временем установления счетчика tуст. Обратная величина, равная
tразр.сч= 1/ Fmax., называется разрешающей способностью. Под разрешающей способностью понимают минимальное время между двумя входными сигналами, в течении которого еще не возникают сбои в работе. Время установления кода tуст равно времени между моментом поступления на вход очередного счетного импульса и переходом всех триггеров счетчика в новое состояние. Счетчики реализуются на Т-триггерах, а также двухступенчатых D-триггерах и универсальных JK-триггерах. По способу организации переносов между триггерами счетчики делятся на счетчики с последовательным, параллельным и последовательно–параллельным переносом. Символом счетчиков на схемах служат буквы СТ (от англ. Сounter – счетчик). При необходимости после символа проставляют число, характеризующее модуль счета (например, 2, 2/5, 2/6, 2/10). В обозначениях микросхем символом счетчика служат буквы ИЕ.
17.1 Двоичные суммирующие счетчики с последовательным
переносом
Двоичные счетчики строятся на счетных триггерах, на триггерах типа D, тактируемых фронтом и переведенных в счетный режим, а также на универсальных JK-триггерах. Триггеры включаются последовательно: выход предыдущего соединяется со счетным входом последующего, цепи начальной установки объединяются. Информация снимается, как правило, с прямых выходов триггеров, выходной сигнал (сигнал переноса) – с выхода последнего триггера. На рисунке 17.1, а, б приведена функциональная схема трехразрядного двоичного суммирующего счетчика, выполненного на Т-триггерах (рисунок 17.1, а), и его условное графическое изображение (рисунок 17.1,б).
Приведем счетчик к исходному нулевому состоянию, путем подачи на асинхронный вход R импульса положительной полярности: Y1: СЧ(4): = 0, при этом счет импульсов прекращается, а на выходах Q4–Q1 установится логический ноль. На счетный вход С первого триггера подадим последовательность тактовых импульсов. По функциональному обозначению входа С видно, что переключение триггера возможно только в моменты перехода сигнала из состояния «1» в «0» (перепад 1/0, срез импульса).
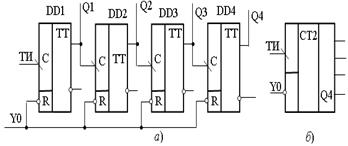
Рисунок 17.1 – Функциональная схема:
а − двоичного счетчика; б − условное графическое обозначение
Счетчик должен работать в режиме суммирования, то есть должна выполняться микрооперация прибавления единицы к содержимому счетчика: Y2: СЧ(4): = СЧ(4) + 1.
Таблица 17.1
| ai | Pi | Si | Pi+1 |
Сложение ведется по правилам двоичной арифметики в соответствии с таблицей 17.1. Пусть последовательность чисел в двоичном счетчике описывается совокупностью четырехразрядных двоичных чисел – a4a3a2a1. Сопоставим каждому разряду числа аi двоичное число на выходе Qi. Исходное состояние триггера будем описывать значением аi, входной сигнал (сигнал переноса из предыдущего разряда) – Pi, результат сложения – Оi и перенос в следующий разряд – Pi+1. Причем следует помнить, что весовая функция сигнала переноса всегда равна двум единицам младшего разряда. Поэтому весовая функция первого разряда – 1, второго – 2, третьего – 4 и четвертого – 8. Такой код называют нормально взвешенным и отмечают как 8-4-2-1 (таблица 17.2).
С приходом первого импульса в счетчике фиксируется первая единица, так как значение суммы в соответствии с таблицей 17.1 будет  . Перенос в следующий разряд будет отсутствовать, поскольку он формируется по правилу Pi +1 = ai Pi. Перенос во второй триггер возникает с приходом второго ТИ (рисунок 17.2). Третий триггер переключается в момент прихода на вход счетчика каждого четвертого импульса. Четвертый триггер включается в момент прихода восьмого тактового импульса.
. Перенос в следующий разряд будет отсутствовать, поскольку он формируется по правилу Pi +1 = ai Pi. Перенос во второй триггер возникает с приходом второго ТИ (рисунок 17.2). Третий триггер переключается в момент прихода на вход счетчика каждого четвертого импульса. Четвертый триггер включается в момент прихода восьмого тактового импульса.
После пятнадцатого импульса все триггеры оказываются в единичном состоянии (a4 a3 а2 a1 = 11112). Шестнадцатый импульс возвращает все триггеры в исходное нулевое состояние, на этом заканчивается первый счетный цикл и процесс повторяется.
Число импульсов поступивших на вход счетчика определяется как М = a4 Q4 + a3 Q3 + a2 Q2 + a1 Q1,
где Q4–Q1 – двоичные числа (0 или 1) в соответствующих разрядах кодовой комбинации, a4 –a1 – весовые коэффициенты этих разрядов (8-4-2-1).
Таблица 17.2 – Таблица истинности
двоичного счетчика
| N | Q4 | Q3 | Q2 | Ql |
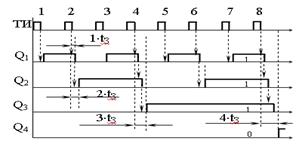
Рисунок 17.2 – Эпюры напряжений двоичного счетчика
Например, по временным диаграммам видим, что состояние на выходах счетчика Q4= 0, Q3= Q2= Q1= 1, откуда следует вывод, что на его вход поступило семь тактовых импульсов:
М = 8 ´ 0 + 4 ´ 1 + 2 ´ 1 + 1 ´ 1 = 7.
Более удобной и компактной формой описания закона функционирования цифрового устройства (счетчика) по сравнению с эпюрами напряжений является таблица истинности (таблица 17.2). Основным достоинством двоичных счетчиков с последовательным переносом является исключительная простота функциональной cхемы и, как следствие, высокая надежность. Двоичные счетчики можно использовать как делители частоты, в том числе при использовании различных вариантов обратных связей. В режиме деления частоты у счетчика используется выходной сигнал только последнего триггера, а промежуточные состояния остальных триггеров не учитываются. Любой счетчик может быть использован в качестве делителя частоты, в связи с чем такое устройство будет называться счетчиком-делителем. Такие делители имеют целочисленный коэффициент деления. Современная элементная база позволяет строить делители с дробными коэффициентами деления.
Счетчики-делители в виде самостоятельных изделий имеются в составе всех серий цифровых микросхем, причем номенклатуру счетчиков отличает большое разнообразие. Многие счетчики обладают универсальными свойствами и позволяют управлять коэффициентом и направлением счета, вводить до начала счета исходное число, останавливать счет по команде, наращивать число разрядов. С помощью готовых счетчиков можно решать большинство практических задач.
17.2 Вычитающие двоичные счетчики
Для перевода двоичного суммирующего счетчика в режим вычитания достаточно сигнал переноса взять с инверсного выхода каждого предыдущего триггера, а информацию о состоянии счетчика по-прежнему снимать с прямых выходов триггеров (рисунок 17.3). Как и в суммирующем счетчике, сигнал начальной установки подается на входы R всех триггеров, счетные импульсы ТИ поступают на вход первого триггера.
Таблица 17.3
| ai | Pi | Qi | Pi+1 |
Микрооперация, выполняемая счетчиком Y1, CЧ(4) = CЧ(4) – 1; функционирование i-го разряда вычитающего счетчика можно описать логическими выражениями переноса Рi+1 и разности Si из таблицы 17.3.
Из таблицы 17.3 следует, что разность Qi формируется в соответствии с логическим выражением:
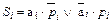 ,
,
где аi – исходный код триггера, Рi – сигнал заема, приходящий на вход триггера.
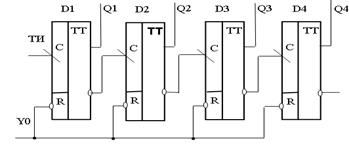
Рисунок 17.3 – Функциональная схема вычитающего счетчика
Формула для получения разности совпадает с выражением, полученным ранее для суммы, поэтому перенос должен подаваться на счетный вход триггера Т, сигнал заема описывается выражением Pi+1 = ai Pi. Диаграммы напряжений вычитающего счетчика приведены на рисунке 17.4.
После первого тактового импульса включается первый триггер. Перепад 1/0 возникающий на выходе `Q1, поступает на вход второго триггера и включает его. Аналогично происходит перенос из второго триггера в третий и далее в четвертый (таблица 17.4), в результате чего после первого импульса счетчик оказывается в состоянии а0а3а2а1=1111 (N=15). С приходом каждого очередного импульса сумма в счетчике уменьшается на единицу. После 16-го импульса счетчик обнуляется. На выходе Q4 формируется сигнал переноса.
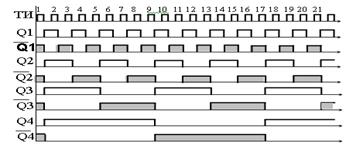
Рисунок 17.4 – Временные диаграммы двоичного
вычитающего счетчика
Основным недостатком двоичных счетчиков с последовательным переносом является то, что в худшем случае новое состояние n-разрядного счетчика устанавливается с задержкой nt3, где t3 –время переключения триггера. Для уменьшения времени распространения могут использоваться счетчики с параллельным переносом. На рисунке 17.5 представлена схема синхронного двоичного счетчика с параллельным переносом информации. В ее основу положены JK-триггеры со встроенной логикой (J1-J2-J3, К1-К2-КЗ). Тактовый импульс поступает на счетные входы триггеров параллельно (синхронно), т. е. одновременно. Входы начальной установки триггеров объединены и управляются сигналами нулевого уровня. Первый триггер счетчика работает в обычном режиме деления на два, и на его управляющих входах J, K стоят уровни лог. 1.
Таблица 17.4 Таблица иистинности двоичного
вычитающего счетчика
| N | Q4 | Q3 | Q2 | Ql |
17.3 Двоичные счетчики с параллельным переносом
Разрешение на перенос сигнала во второй триггер дает триггер D1: Р2 = Q1, т. е. при единичном уровне на J2 = K2 возможно переключение триггера D2 в противоположное состояние. В свою очередь разрешение на перенос в третий триггер имеет вид логического выражения Р3 = Q1×Q2. Для реализации этой функции входы J3 и К3 попарно объединены.
Логическое выражение, формирующее разрешение на перенос в четвертый триггер, – P4 = Q3Q2Ql, в связи с чем попарно объединены между собой J1 и К1, J2 и К2, J3 и К3 этого триггера.  Трехвходовую логику по J и К имеет только триггер К155ТВ1, который можно использовать для построения синхронных счетчиков без использования внешней логики. Известные триггеры других серий не имеют достаточной внутренней логики по входам JK, и при построении синхронных счетчиков приходится использовать дополнительную логику (рисунок 17.6).
Трехвходовую логику по J и К имеет только триггер К155ТВ1, который можно использовать для построения синхронных счетчиков без использования внешней логики. Известные триггеры других серий не имеют достаточной внутренней логики по входам JK, и при построении синхронных счетчиков приходится использовать дополнительную логику (рисунок 17.6).
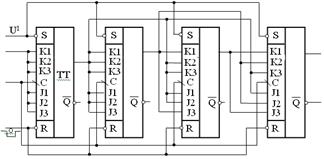
Рисунок 17.5 – Функциональная схема двоичного
синхронного счетчика на триггерах со встроенной логикой
Счетчик приводится к исходному нулевому состоянию с помощью сигнала «УO», поступающего на входы R. Счетные входы С триггеров объединены, и на них подаются входные импульсы одновременно. Процессом переключения триггеров управляют входы JK триггеров, также попарно объединенных. Логические выражения для переносов будут иметь вид П1=1; П2=Q1; ПЗ=Q2 Q3; П4=Q3 Q2 Q1. Для реализации функций переносов недостаточно внутренней логики триггеров по входам JK. В связи с этим на входе третьего триггера устанавливается двухвходовая ячейка И, а на входе четвертого – трехвходовая. Временные диаграммы счетчика соответствуют временным диаграммам двоичного счетчика с последовательным переносом с той лишь разницей, что задержка появления входного сигнала на любом выходе постоянна и равна tзад. Дальнейшее наращивание числа разрядов становится нецелесообразным в виду усложнения схемы. Поэтому при построении счетчиков используются схемы с параллельно–последовательным переносом. Схема счетчика с последовательно-параллельным переносом состоит из групп триггеров, внутри каждой из которых организуется параллельный перенос, а между группами – последовательный.
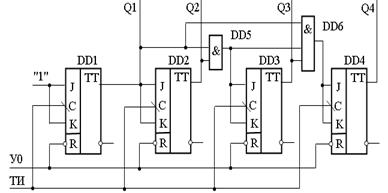
Рисунок 17.6 – Функциональная схема двоичного синхронного счетчика
17.4 Реверсивный двоичный счетчик
В реверсивном двоичном счетчике объединяются схемы суммирующего и вычитающего счетчика, при этом предусмотрены логические цифровые схемы, позволяющие управлять направлением счета. В реверсивном двоичном счетчике с параллельным переносом, выполненном на Т-триггерах (рисунок 17.7), счетные сигналы поступают на вход каждого Т-триггера через логические схемы И-И-ИЛИ. Управление организовано таким образом, что при суммирование сигналы переноса берутся с прямых выходов Qi триггеров, а при вычитании – с инверсных`Qi.
Если счетчик работает как суммирующий, счетные импульсы следует подавать на вход «+1», при этом на входе «–1» следует установить нулевой уровень. Нулевой уровень на шине приводит к тому, что логические ячейки И5, И6, И7, И8 оказываются заблокированными и выходные сигналы с инверсных выходов триггеров не могут передаться на счетные входы триггеров. Счетные импульсы со входа «+1» в виде прямоугольных импульсов поступают на логические ячейки И1, И2, ИЗ, И4 одновременно. Первый триггер как в режиме суммирования, так и в режиме вычитания переключается с приходом заднего фронта (среза) каждого тактирующего импульса. Второй триггер срабатывает при условии, если Q1=1, третий триггер готов к работе при Q1Q2=1, и четвертый триггер – при Q1Q2Q3=1. На выходе счетчика установлена схема И9, выходной сигнал которой обозначен ³ 15.
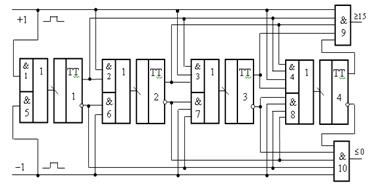
Рисунок 17.7 – Функциональная схема двоичного
реверсивного счетчика
На этом выходе формируется сигнал переноса в следующий (старший) разряд, когда все триггеры счетчика установятся в единичное состояние (Q1Q2Q3Q4 =1). В режиме вычитания в работу включены логические ячейки И5, И6, И7, И8, и переносы между триггерами осуществляются через эти ячейки. На выходе установлена логическая ячейка И10, выход которой обозначен £0.

Рисунок 17.8 – Условное изображение: а − реверсивного счетчика; б − функциональная схема реверсивного счетчика с одним счетным входом
Сигнал переноса на выходе этой ячейки формируется, когда на прямых выходах триггеров установятся нули, а произведение 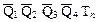 станет равным 1. Условное обозначение реверсивного счетчика приведено на рисунке 17.8, а. Если требуется построить реверсивный счетчик с одним источником счетных сигналов, то необходимо предусмотреть на входе счетчика устройство, переключающее эти сигналы на суммирование «+1» или вычитание «–1» (рисунок 17.8, б).
станет равным 1. Условное обозначение реверсивного счетчика приведено на рисунке 17.8, а. Если требуется построить реверсивный счетчик с одним источником счетных сигналов, то необходимо предусмотреть на входе счетчика устройство, переключающее эти сигналы на суммирование «+1» или вычитание «–1» (рисунок 17.8, б).
17.5 Десятичный счетчик
Функциональная схема двоично-десятичного счетчика, выполненного на JK-триггерах и работающего с естественными весами кодов 8-4-2-1, показана на рисунке 17.9, а. Условное графическое изображение счетчика приведено на рисунке 17.9, б.
В исходное состояние счетчик приводится импульсом начальной установки У0 низкого уровня, подаваемого на входы R триггеров. Тактовые импульсы подаются на вход С первого триггера, находящегося в счетном режиме, поскольку на его входах управления J1 и K1 установлена лог. 1. C прямого выхода первого триггера импульсы подаются на счетные входы второго и четвертого триггеров.
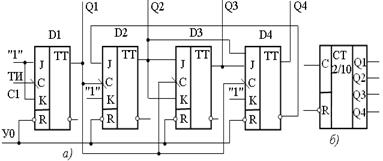
а − функциональная схема; б − условное графическое
обозначение
Рисунок 17.9 – Двоично-десятичный счетчик
При поступлении на вход счетчика первых восьми импульсов декада работает как обычный двоичный суммирующий счетчик. Это объясняется тем, что второй триггер также находится в «режиме деления на два», так как J2=К2 =1. На входе К2 второго триггера постоянно установлен высокий уровень напряжения U1, а на входе J2 вплоть до прихода восьмого импульса уровень лог. 1 подается с инверсного выхода  четвертого триггера. Третий триггер работает в режиме «деления частоты на два» (J3 =K3 = Q2). Четвертый триггер находится в режиме управления нулем (J4 = 0, К4=1) и вплоть до восьмого на тактирующие импульсы не реагирует (рисунок 17.10).
четвертого триггера. Третий триггер работает в режиме «деления частоты на два» (J3 =K3 = Q2). Четвертый триггер находится в режиме управления нулем (J4 = 0, К4=1) и вплоть до восьмого на тактирующие импульсы не реагирует (рисунок 17.10).
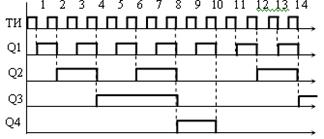
Рисунок 17.10 – Эпюры напряжений двоично-десятичного
Счетчика
К моменту поступления восьмого импульса на входах J4&J4 четвертого триггера устанавливаются уровни лог.1 (J4=К4 =1), и триггер переходит в счетный режим. Восьмой импульс выключит первый, второй и третий триггеры, а четвертый триггер переведет в единичное состояние, в результате чего на его инверсном выходе  установится низкий уровень напряжения. Уровень лог. 0 по цепи обратной связи поступит на вход J2 второго триггера и переведет его в режим управления нулем. Девятый импульс включает первый триггер, десятый импульс выключает его и одновременно перепад 1/0 с выхода первого триггера выключает четвертый триггер, т.к. на его входах J4 установились уровни низкого напряжения и он перешел в режим управления нулем (J4 = 0, К4 = 1).
установится низкий уровень напряжения. Уровень лог. 0 по цепи обратной связи поступит на вход J2 второго триггера и переведет его в режим управления нулем. Девятый импульс включает первый триггер, десятый импульс выключает его и одновременно перепад 1/0 с выхода первого триггера выключает четвертый триггер, т.к. на его входах J4 установились уровни низкого напряжения и он перешел в режим управления нулем (J4 = 0, К4 = 1).
17.6 Типовые счетчики
17.6.1 Асинхронные счетчики с последовательным переносом
Cуммирующие счетчики-делители К555ИЕ2, К155ИЕ4, К555ИЕ5 близки по логическим структурам и принципу действия: каждая микросхема содержит четыре триггера, определенным образом связанных между собой. В каждой микросхеме один из триггеров имеет отдельный вход и прямой выход, три оставшихся триггера соединены так, что образуют делитель на 8 в МСХ ИЕ5, делитель на 6 в МСХ К155ИЕ4 и на 5 в ИЕ2 (рисунок 17.11).
МикросхемаК155ИЕ2 – это четырехразрядный двоично-десятичный счетчик, состоящий из четырех Т-триггеров, внутренне соединяемых для выполнения операций деления на два и пять (рисунок 17.12).
Входы установки нуля R0(0), R0(1) обеспечивают при высоком уровне сигнала одновременно на обоих входах и нулевом уровне хотя бы на одном из входов R9 возвращение выходов триггеров Q1– Q4 в состояние низкого уровня и запрещения счета по входам С1, С2. Вход Q1 не соединен с последующими триггерами, поэтому можно осуществить три независимых режима работы счетчика.
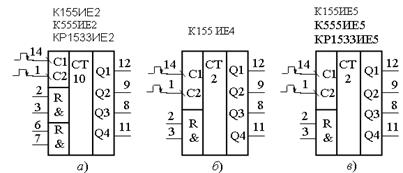
а − счетчик ИЕ2; б − счетчик ИЕ4; в − счетчик ИЕ5
Рисунок 17.11 – Условное графическое изображение ИС
При подаче тактовых импульсов на С1(14) и внешнем соединении Q1(12) c C2(1) выполняется операция двоично-десятичного счета (0…9) в коде 8-4-2-1. Первый триггер понижает входную частоту в два раза, второй – четвертый триггеры производят деление на 5 (таблица 17.5).
Если тактовые импульсы подавать на вход С2(1), а Q4(11) соединить со входом С1(14), то счетчик по-прежнему будет выполнять операцию десятичного счета, но на выходе Q1(12), будет формироваться меандр, а весовые функции кода будут 5-4-2-1 (Q1 Q4 Q3 Q2) (таблица 17.6).
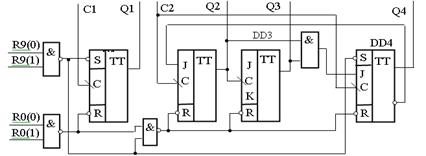
Рисунок 17.12 – Функциональная схема двоичного счетчика К555ИЕ2
Таблица 17.5
| N | Q4 | Q3 | Q2 | Q1 |
Таблица 17.6
| N | Q1 | Q4 | Q3 | Q2 |
Дата добавления: 2020-03-17; просмотров: 3079;











