Динамические характеристики резинометаллических опорных частей
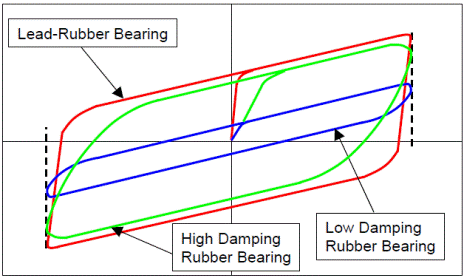
Характеристики резинометаллических опорных частей определяются в результате динамических испытаний, при которых опорные части подвергаются постоянной вертикальной нагрузке и гармонической поперечной силе. На Рис.10.4.5. представлены схемы приложения нагрузок для определения демпфирующих свойств резинометаллических опорных частей. В результате такого рода испытаний определяются петли гистерезиса, площади которых пропорциональны энергии, рассеиваемой опорной частью за цикл колебаний. На Рис.10.4.6. представлены петли гистерезиса резинометаллических опорных частей различного типа, определённые экспериментальным путём.

Рис.10.4.5. Схемы приложения нагрузок для определения демпфирующих свойств опорных частей
|
|
|
Перемещение
Рис. 10.4. 5. Гистерезисные кривые опорных частей различного типа:
LDRB – резинометаллические опорные части из натуральной или синтетической резины с малым коэффициентом демпфирования,
HDRB - резинометаллические опорные части из натуральной или синтетической резины с большим коэффициентом демпфирования,
LRB - резинометаллические опорные части из резины с малым коэффициентом демпфирования и свинцовым стержнем.


Рис.10.4.6. Фотография, полученная при испытании резинометаллической опорной части
Характеристики резинометаллических опорных частей получают в результате испытаний на гармонические воздействия. При таких испытаниях опорные части подвергаются постоянным сжимающим нагрузкам, а верхней плите задаются периодические поперечные перемещения с заданной частотой и амплитудой: 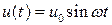 .
.
Если опорные части моделируются упруго-вязкими элементами, упругие силы, возникающие в опорных частях, пропорциональны перемещениям, а демпфирующие силы пропорциональны скоростям. Результирующая, (измеряемая в экспериментах) сила зависит и от перемещения, и от скорости.
При этом производятся измерения сил, вызывающих эти перемещения. При наличии демпфирования силы не совпадают по фазе с перемещениями, поэтому можно предположить, что выражение для силы имеет вид:
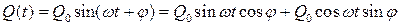 . (10.4.1).
. (10.4.1).
Преобразуем эту формулу, используя выражение для перемещений:
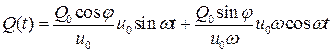 . (10.4.2)
. (10.4.2)
или
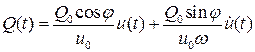 . (10.4.3)
. (10.4.3)
Демпфирующая сила смещена по фазе относительно упругой силы на величину 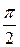 .
.
Таким образом, результирующую силу можно представить в виде:
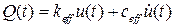 . (10.4.4)
. (10.4.4)
Для определения параметров 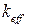 и
и 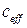 используют график зависимости поперечной силы от перемещения, полученный при испытании резинометаллической опорной части (Рис.10.4.5).
используют график зависимости поперечной силы от перемещения, полученный при испытании резинометаллической опорной части (Рис.10.4.5).
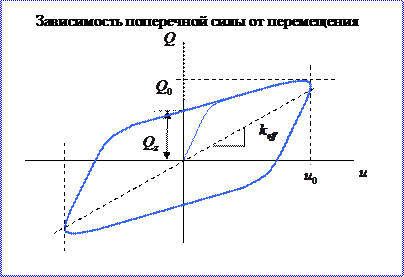
Рис.10.4.7. Типичная диаграмма, полученная при испытании резинометаллической опорной части.
Из уравнения (10.4.2) при 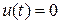 следует:
следует: 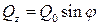 , таким образом, фазовый угол смещения силы относительно перемещения определяется формулой:
, таким образом, фазовый угол смещения силы относительно перемещения определяется формулой: 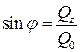 .
.
Учитывая выражения (4.2) и (4.3), получим:
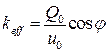 ,
, 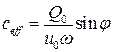 . (10.4.6)
. (10.4.6)
Относительный коэффициент демпфирования можно найти, используя выражение для фазового угла: 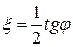 .
.
В последние годы в англоязычной технической литературе для описания поведения элементов, обладающих упругими и вязкими свойствами, используются понятия: «накопительная жёсткость» (storage stiffness), от которой зависит величина запасаемой энергии, и «потерянная жёсткость» (loss stiffness), от которой зависит величина рассеиваемой энергии. Эти параметры определяются выражениями:
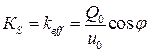 и
и 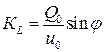 или
или 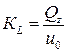 . (10.4.7).
. (10.4.7).
Коэффициент демпфирования определяется по формуле
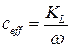 (10.4.8)
(10.4.8)
«Накопительная жёсткость» характеризует опорную часть с точки зрения накопления энергии другими словами определяет упругие свойства, в то время как «потерянная жёсткость» характеризует опорную часть с точки зрения рассеяния энергии. Фазовый угол характеризует соотношение между запасаемой и рассеиваемой энергией.
Если фазовый угол равен 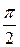 , это говорит о том, что опорная часть не запасает энергию, т.е. представляет собой демпфер, характеризующийся параметрами:
, это говорит о том, что опорная часть не запасает энергию, т.е. представляет собой демпфер, характеризующийся параметрами:
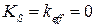 ,
, 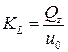 и
и 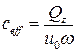 (10.4.9)
(10.4.9)
И наоборот, если фазовый угол равен нулю, опорная часть не рассеивает энергию, т.е. опорная часть представляет собой упругий элемент (линейную пружину):
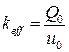 ,
, 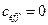 (10.4.10)
(10.4.10)
В общем случае жёсткость пружины, эквивалентной жёсткости опорной части определяется тангенсом угла наклона петли гистерезиса. Угол наклона петли гистерезиса определяется углом наклона прямой, проведённой через точки петли, соответствующим максимальным перемещениям.
Ширина петли гистерезиса при 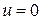 пропорциональна «потерянной жёсткости». Площадь петли гистерезиса, которая также пропорциональна «потерянной жёсткости», равна энергии, рассеиваемой за один цикл колебаний.
пропорциональна «потерянной жёсткости». Площадь петли гистерезиса, которая также пропорциональна «потерянной жёсткости», равна энергии, рассеиваемой за один цикл колебаний.
Используя экспериментальную петлю гистерезиса, можно получить зависимости между модулями упругости при сдвиге и деформациями сдвига вязкоупругой опорной части.
В этом случае также удобно использовать два параметра, характеризующих жёсткость при сдвиге опорной части при гармоническом нагружении. Модуль сдвига 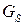 , от которого зависит величина запасаемой энергии, и модуль
, от которого зависит величина запасаемой энергии, и модуль 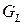 , от величины которого зависит рассеваемая энергия.
, от величины которого зависит рассеваемая энергия.
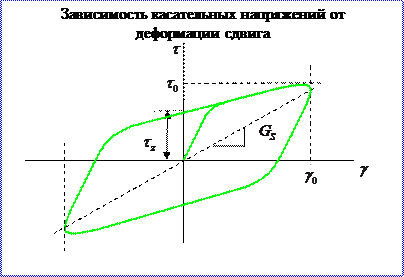
Рис.10.4.8. Зависимость касательных напряжений от деформаций
сдвига при гармоническом нагружении
Учитывая, что параметры 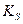 и
и 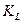 , можно представить в виде:
, можно представить в виде:
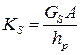 ,
, 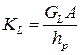 (10.4.11)
(10.4.11)
где А- площадь поперечного сечения опорной части,
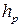 - общая толщина резиновых слоёв,
- общая толщина резиновых слоёв,
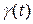 - деформация сдвига,
- деформация сдвига,
уравнение (4.4) можно представить в виде:
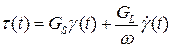 (10.4.12)
(10.4.12)
Ширина петли гистерезиса при 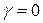 пропорциональна модулю сдвига
пропорциональна модулю сдвига  , который в свою очередь пропорционален «потерянной жёсткости». Модуль сдвига
, который в свою очередь пропорционален «потерянной жёсткости». Модуль сдвига 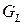 определяет величину рассеиваемой энергии. Площадь петли гистерезиса пропорциональна модулю
определяет величину рассеиваемой энергии. Площадь петли гистерезиса пропорциональна модулю 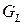 и равна энергии, рассеиваемой за один цикл колебаний.
и равна энергии, рассеиваемой за один цикл колебаний.
Модуль сдвига 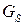 характеризует максимальную величину, запасаемой энергии. Следует отметить такой важный факт, что модули
характеризует максимальную величину, запасаемой энергии. Следует отметить такой важный факт, что модули 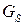 и
и 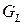 характеризуют свойства материала в отличие от параметров
характеризуют свойства материала в отличие от параметров 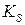 и
и 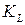 , которые зависят от конструктивных особенностей опорных частей (площади резиновых слоёв А, общей толщины резиновых слоёв
, которые зависят от конструктивных особенностей опорных частей (площади резиновых слоёв А, общей толщины резиновых слоёв 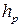 ).
).
Фазовый угол между силой, пропорциональной деформации сдвига и силой, пропорциональной скорости деформации сдвига, определяется из отношения: 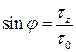 .
.
Коэффициент потерь (зависит от частоты): 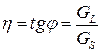 .
.
Относительный коэффициент демпфирования: 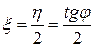 .
.
Дата добавления: 2016-06-18; просмотров: 3425;











