Условия статической определимости кинематической цепи

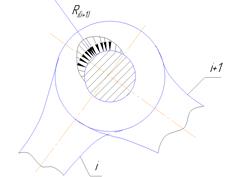В плоской кинематической цепи существуют только кинематические пары 5-го и 4-го класса. Рассмотрим вращательную кинематическую пару 5-го класса.

В первом приближении будем вести расчёт без учёта сил трения в парах. Во вращательной паре результирующая сила реакции R_i(i+1) проходит через центр шарнира. Величина и направление этой реакции неизвестна, так как они зависят от величины и направления заданных сил, приложенных к звеньям пары. Таким образом, вращательная пара вносит в общее число неизвестных параметров – два, и один параметр здесь известен.

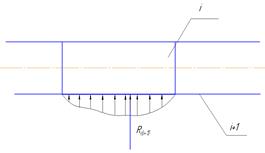Рассмотрим поступательную кинематическую пару 5-го класса

В поступательной паре 5-го класса реакция перпендикулярна оси поступательной пары, но точка её приложения и величина неизвестны, т.е., как и в предыдущем случае – два параметра неизвестны, а один параметр известен.

Рассмотрим высшую пару 4-го класса.

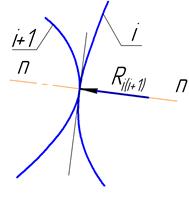В высшей паре реакция приложена в точке контакта элементов высшей пары (точка соприкосновения звеньев) и направлена по общей нормали n-n, проведённой в точке соприкосновения. Неизвестным параметром остается величина реакции, т.е., в высшей паре один параметр неизвестен и два параметра известны.

Составим уравнение статической определимости плоских кинематических цепей. Так как для каждого звена, имеющего плоскопараллельное движение, можно составить три уравнения равновесия, то число уравнений, которое мы можем составить для n звеньев, будет равно 3n. Число неизвестных, которое необходимо определить, будет равно для пар 5-го класса 2Р₅ и для пар 4-го класса – Р₄. Следовательно, кинематическая цепь будет статически определима, если удовлетворяется условие 3n = 2Р₅ –Р₄ или 3n- 2Р₅ –Р₄ = 0

Это значит, что любая структурная группа Ассура, сколь бы сложной она не была, обладает замечательным свойством: она статически определима.

После того, как силовой расчёт всех структурных групп проделан, ведущее звено получает статическую определимость, следовательно, статически определим и весь механизма.

На основании выше изложенного можно сформулировать общую методику силового расчёта: силовой расчёт механизма следует проводить по структурным группам, начиная от группы, наиболее удалённой от первичного механизма и заканчивая расчёт самим первичным механизмом.