Задача об оптимальном составе смеси
Этот обширный класс задач включает в себя так называемые задачи на составление смесей или задачи на использование заменителей.
Задача составления экономичной шихты для выплавления чугуна и стали, а также получения смесей для металлокерамических изделий.
При получении легированной стали необходимо использовать шихту определенного химического состава , многие элементы шихты достаточно дороги, и вместе с тем в ее состав входят малоценные материалы ( чугун, лом и т.д. ).
Ставится задача выбора шихты минимальной стоимости, в состав которой должны входить в заданных количествах необходимые химические вещества.
Пусть имеется n-видов компонентов шихты, каждый из которых содержит в различных пропорциях m-видов необходимых химических веществ.
Известно, что в единице компонента j-го вида ( j=1…n ) содержится 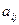 единиц
единиц
химического вещества i( i=1…m ).
Минимальная потребность в i-том веществе составляет 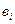 единиц.
единиц.
Себестоимость производства единицы продукции шихты j-го вида равна 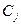 , а выдаваемый объем ограничен величиной
, а выдаваемый объем ограничен величиной 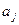 .
.
Требуется выбрать такой состав, чтобы количество каждого компонента было не меньше требуемого, а суммарная стоимость была минимальна.
Обозначим через 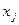 ( j=1…n ) количество единиц вещества j-го вида. Тогда общее количество i-го химического элемента содержащегося в составе данного компонента шихты выразится суммой:
( j=1…n ) количество единиц вещества j-го вида. Тогда общее количество i-го химического элемента содержащегося в составе данного компонента шихты выразится суммой:
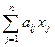 (1)
(1)
Эта сумма не должна быть меньше необходимого минимального 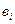 по всем видам химического вещества:
по всем видам химического вещества:
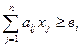 ( i=1…m ) (2)
( i=1…m ) (2)
Вместе с тем потребление каждого компонента ограничено имеющимися запасами 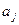 :
:
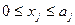 ( j=1…n ) (3)
( j=1…n ) (3)
Суммарная стоимость шихты:
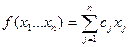 (4)
(4)
Таким образом, оптимальным будет такой состав компонентов, который будет обращать в минимум сумму (1) при соблюдении (2) и (3).
Задача о планировании производства
Есть завод, выпускающий n видов продукции, для производства которого используется m видов сырья. На производство j-го вида продукции идет ai,j единиц i-го сырья. Цена единицы j-ой продукции сj , запас i-го вида сырья bi. Составить план производства продукции, который дает максимальный доход от реализации. Если обозначить xj – план производства, то математическая постановка задачи, для решения поставленной проблемы имеет вид:
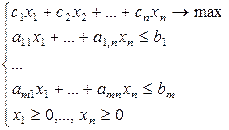
Дата добавления: 2020-02-05; просмотров: 311;











