Критерий устойчивости Михайлова

<8 9 101112 13 14 >

Этот критерий устойчивости, сформулированный в 1938 г. советским ученым А.В. Михайловым, является, по существу, геометрической интерпретацией принципа аргумента и позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Пусть дано характеристическое уравнение системы

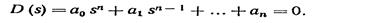
Левую часть характеристического уравнения называют характеристическим полиномом

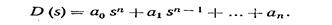(14.6)

Если подставить в этот полином чисто мнимое значение s = jω, то получим комплексный полином

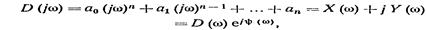(14.7)

где

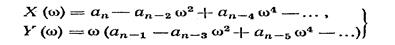(14.8)

называют соответственно вещественной и мнимой функциями Михайлова; функции D(ω) и ψ(ω) представляют собой модуль и фазу (аргумент) вектора D(jω).

При изменении частоты ω вектор D(jω), изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.

В соответствии с (14.5) угол поворота вектора D(jω) вокруг начала координат при изменении частоты ω от 0 до ¥ равен

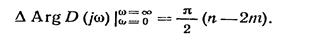
Отсюда определяем число правых корней полинома D(s), т. е.

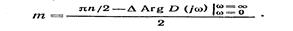(14.9)

Из (14.9) видно, что число правых корней т будет равно нулю при одном-единственном условии

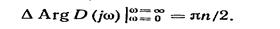(14.10)

Условие (14.10) является необходимым, но не достаточным условием устойчивости. Для устойчивости системы необходимо и достаточно, чтобы все п корней характеристического уравнения были левыми; иначе говоря, среди них не должно быть корней, лежащих на мнимой оси и обращающих в нуль комплексный полином D(jω), т. е. должно выполняться еще одно условие

D(jω) ≠ 0. (14.11)

Формулы (14.10) и (14.11) представляют математическое выражение критерия устойчивости Михайлова: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы вектор кривой Михайлова D(jω) при изменении ω от 0 до ¥ повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на угол πп/2, где п — порядок характеристического уравнения.

Заметим, что для устойчивых систем кривая Михайлова начинается при ω= 0 на вещественной положительной полуоси, поскольку при а₀ > 0 все коэффициенты характеристического уравнения положительны и D(0) = а_n > 0. Кроме того, для устойчивых систем, описываемых обыкновенными дифференциальными уравнениями с постоянными коэффициентами, фаза (аргумент) ψ(ω) с ростом частоты ω должна возрастать монотонно, т. е. вектор D (jω) должен поворачиваться только против часовой стрелки, поскольку с ростом частоты монотонно возрастают имеющие одинаковые (положительные) знаки фазы элементарных векторов (jω - s_i), являющиеся слагаемыми фазы вектора D(jω).

Учитывая сказанное выше, критерий устойчивости Михайлова можно сформулировать так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты ω от 0 до ¥, начинаясь при ω = 0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов координатной плоскости, где п — порядок характеристического уравнения.

Кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического уравнения.

На рисунке 14.3. показаны типичные кривые Михайлова для устойчивых систем, описываемых уравнениями, начиная от первого (п = 1) и кончая пятым (п = 5) порядком. Для удобства сравнения коэффициенты а_n во всех случаях приняты одинаковыми.

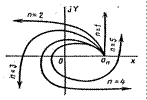
Рисунок 14.3 – Кривые Михайлова устойчивых систем

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора D(jω) оказывается меньше, чем πп/2. Число правых корней неустойчивой системы можно определить по (14.9).

На рисунке 14.4 показаны кривые Михайлова для неустойчивых и нейтральных систем. Рисунок 14.4, а — при ω = 0 кривая Михайлова начинается на отрицательной вещественной полуоси; система неустойчива. Рисунок 14.4, б — порядок уравнения п = 5, а кривая Михайлова находится вся в одном квадранте (этому соответствует характеристическое уравнение D(s)= a₀s⁵ + a₁s⁴ + а₂ = 0); система неустойчива. Рисунок 14.4, в — нарушена последовательность прохождения квадрантов; система неустойчива. Рисунок 14.4, г—кривая Михайлова начинается в начале координат, т. е. в характеристическом уравнении имеется по крайней мере один нулевой корень; система находится на границе апериодической устойчивости; небольшая деформация кривой Михайлова (прерывистая линия) делает систему устойчивой. Рисунок 14.4, д — кривая Михайлова проходит при некотором значении частоты ω_k через начало координат, т. е. в характеристическом уравнении имеются чисто мнимые корни ± jω_k; система находится на границе колебательной устойчивости; небольшая деформация кривой Михайлова делает систему устойчивой (прерывистая линия). Рисунок 14.4, е — кривая Михайлова проходит через начало координат, но небольшой деформацией кривой Михайлова удовлетворить условиям устойчивости нельзя; система неустойчива. Построение кривой Михайлова практически производится либо методом контрольных точек, либо методом вспомогательных годографов.

Первый метод сводится к определению ряда точек кривой Михайлова, соответствующих фиксированным значениям частоты ω, включая (обязательно) частоты точек пересечения кривой с осями координат, которые находятся как корни уравнений (14.12) и (14.13). При втором методе предварительно определяют годографы отдельных звеньев системы и по ним строят искомую кривую Михайлова, применяя правила умножения и сложения векторов.

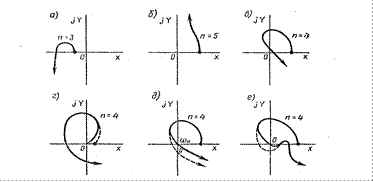
Рисунок 14.4 - Кривые Михайлова неустойчивых систем

<8 9 101112 13 14 >

Дата добавления: 2022-07-20; просмотров: 167;

Поиск по сайту