Критерий устойчивости Найквиста. Запас устойчивости
Критерий устойчивости Найквиста для статических систем
Этот частотный критерий устойчивости, разработанный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики разомкнутой системы.
Пусть передаточная функция разомкнутой системы
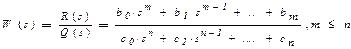 (15.1)
(15.1)
Подставляя в (15.1) s = jω, получаем частотную передаточную функцию разомкнутой системы:
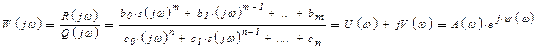
где U(ω) и Y(ω) — действительная и мнимая части частотной передаточной функции соответственно; модуль А (ω) и фаза ψ(ω) частотной передаточной функции равны А (ω) = (U2(w) + V2(ω))1/2; ψ (ω)= Arctg(V(ω)/U(ω)).
Если изменять частоту ω от — ¥ до ¥, то вектор W(jω) будет меняться по величине и фазе. Кривую, описываемую концом этого вектора в комплексной плоскости, называют амплитудно-фазовой характеристикой разомкнутой системы (рисунок 15.1).
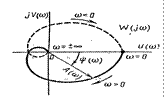
Рисунок 15.1 – Годограф Найквиста (амплитудно-фазовая характеристика разомкнутой системы
Амплитудно-фазовая характеристика симметрична относительно вещественной оси, поэтому обычно вычерчивают только ту часть ее, которая соответствует положительным частотам ω > 0 (сплошная линия на рисунке 15.1), а ветвь этой характеристики, соответствующая отрицательным частотам ω < 0 (пунктирная линия на рисунке 15.1), может быть найдена как зеркальное отражение ветви, соответствующей положительным частотам, относительно вещественной оси. Рассмотрим вспомогательную функцию
φ(s) = 1 + W(s) = 1 + R (s)/Q (s) = [Q (s) + R (s)]/Q (s) = D (s)/Q (s) (15.3)
где D (s) = Q (s) + R (s) = a0sn + a1sn-1 + …+ an — характеристический полином замкнутой системы; Q (s) = c0sn+ c1sn-1 + …+ cn — характеристический полином разомкнутой системы; R (s) = b0sm + b1sm-1 + … + bm - полином степени т.
Заметим, что так как в реальных системах степень полинома R (s) не выше степени полинома Q (s), т. е. т≤n, то степени числителя и знаменателя дроби (15.3) одинаковы и равны п.
Подставляя в (15.3) s = jω, получим
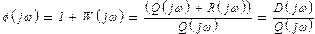 (15.4)
(15.4)
Пусть характеристическое уравнение замкнутой системы D (s) = 0 имеет т правых корней и п — т левых корней, а характеристическое уравнение разомкнутой системы Q (s) =0 имеет l правых и п — l левых корней.
При изменении частоты ω от - ¥ до ¥ изменение угла поворота вектора φ(jω) на основе принципа аргумента будет
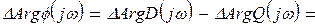
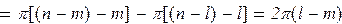 (15.5)
(15.5)
Для устойчивости замкнутой системы необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми, т. е. m= 0. Отсюда суммарный поворот вектора φ(jω) устойчивой системы вокруг начала координат должен быть равен
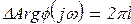 (15.6)
(15.6)
где l — число правых корней характеристического уравнения разомкнутой системы.
Обычно рассматривают только положительные частоты ω > 0, в этом случае угол поворота вектора φ(jω) будет вдвое меньше,т.е.
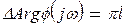 (15.7)
(15.7)
Таким образом, если разомкнутая система является неустойчивой и имеет l правых корней, то замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика вспомогательной функции φ(jω) при изменении частоты ω от 0 до ¥ охватывает начало координат в положительном направлении l/2 раз.
Легко заметить, что число оборотов вектора φ(jω) вокруг начала координат равно числу оборотов вектора W(jω) вокруг точки (—1, j0).
На основании сказанного вытекает следующая формулировка критерия устойчивости Найквиста: если разомкнутая система автоматического управления неустойчива, то, для того чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы W(jω) при изменении частоты ω от 0 до ¥ охватывала точку (—1, j0) в положительном направлении l/2 раз, где l — число правых корней характеристического уравнения разомкнутой системы.
На рисунке 15.2, а показана амплитудно-фазовая характеристика φ(jω), а на рисунке 15.2, б—амплитудно-фазовая характеристика W(jω), соответствующие устойчивой замкнутой системе, которая в разомкнутом состоянии была неустойчива и имела число правых корней l = 2. Обычно в реальных системах W(jω)|ω=¥= 0, и поэтому φ(jω)|ω = ¥ = 1.
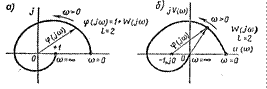
Рисунок 15.2 – Амплитудно-фазовые характеристики φ(jω) и W(jω)
При сложной форме характеристики W(jω) могут возникнуть затруднения при определении числа ее оборотов вокруг критической точки (—1, j0). В этом случае для суждения об устойчивости удобно применять «правило переходов», предложенное Я. 3. Цыпкиным. Назовем переход характеристики W(jω) через отрезок вещественной оси слева от точки (—1, j0), т. е. через отрезок (—¥, —1), при возрастании со положительным, если он происходит сверху вниз, и отрицательным, если он происходит снизу вверх. Если характеристика W(jω) начинается на отрезке (— ¥, —1) при ω = 0 или заканчивается на нем при ω = ¥, то в этих случаях считают, что она совершает полперехода.
Тогда критерий Найквиста можно сформулировать так:
если разомкнутая система автоматического управления неустойчива, то, для того чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов амплитудно-фазовой характеристики разомкнутой системы W (jω) через отрезок вещественной оси (— ¥, —1) при изменении частоты ω от 0 до ¥ была равна l/2, где l — число правых корней характеристического уравнения разомкнутой системы.
Если система автоматического управления в разомкнутом состоянии устойчива, т. е. l = 0, то приращение аргумента вектора φ(jω) равно нулю:
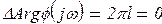 (15.8)
(15.8)
Это означает, что для устойчивости замкнутой системы необходимо, чтобы амплитудно-фазовая характеристика φ(jω) не охватывала начало координат (рисунок 15.3, а), а амплитудно-фазовая характеристика W(jω) не охватывала точку с координатами (—1, j0), (рисунок 15.3, б).
Таким образом, для этого наиболее часто встречающегося на практике случая получаем следующую формулировку критерия Найквиста: если разомкнутая система автоматического управления устойчива, то замкнутая система автоматического управления будет устойчива, если амплитудно-фазовая характеристика разомкнутой системы W(jω) не охватывает точку (—1, j0).
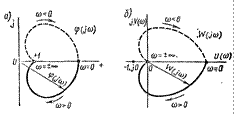
Рисунок 15.3 – Амплитудно-фазовые характеристики устойчивой системы
Дата добавления: 2022-07-20; просмотров: 115;










