Теоретические основы расчета осадок оснований фундаментов
ДЕФОРМЦИИ ГРУНТОВ И РАСЧЕТ ОСАДОК ОСНОВАНИЙ СООРУЖЕНИЙ
Основные положения
В результате строительства сооружения, даже если прочность грунта обеспечена, возникают деформации основания. Как правило, они имеют неравномерный характер и вызывают перераспределение усилий в конструкциях сооружения. При определенных условиях это может затруднить нормальную эксплуатацию сооружения, а в некоторых случаях даже привести к его аварии.
Количественное прогнозирование деформаций системы «сооружение — основание» представляет собой одну из наиболее сложных задач механики грунтов. Поясним это с помощью примера, заимствованного из учебника П. Л. Иванова (рис. 9.1).
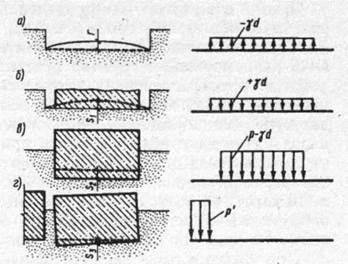
Рис. 9.1. Этапы строительства и эксплуатации сооружения, соответствующие им нагрузки и деформации основания
Первая стадия строительства всегда заключается в отрытии котлована под сооружение. При этом происходит разгрузка грунта ниже поверхности дна котлована на величину γd, где γ — удельный вес грунта, d – глубина котлована и в соответствии с этим подъем дна котлована. Естественно, что чем глубже котлован, тем интенсивнее проявляется разгрузка грунта, причем величина подъема дна будет неравномерной по ширине котлована – наименьшей вблизи подошвы откоса и наибольшей в среднем сечении. Выберем некоторое сечение и обозначим величину подъема через r (рис. 9.1, а). Известно, что процесс разгрузки развивается по закону упругого деформирования, а величина r может быть определена по ветви разгрузки компрессионной кривой.
Следующую стадию строительства – возведение сооружения – можно условно разделить на два этапа: первый – когда нагрузка от строящегося сооружения достигает величины γd, соответствующей весу извлеченного грунта, и второй – когда после завершения строительства нагрузка возрастет еще на величину p – γd, где р – среднее напряжение под подошвой построенного сооружения.
На первом этапе увеличение нагрузки вызовет осадку основания в рассматриваемом сечении на величину s1 от положения дна котлована, определенного его подъемом. Величина этой осадки определится уже по ветви нагружения компрессионной кривой и не будет равной стреле подъема r (рис. 9.1, б). Возрастание нагрузки на втором этапе приведет к дальнейшему увеличению осадки s2 уже от нового положения дна котлована (рис. 9.1, в).
Наконец, после завершения строительства в процессе эксплуатации сооружения возможны дополнительные воздействия (надстройка сооружения, изменение состояния грунтов основания, строительство новых сооружений вблизи построенного и т. п.). Эти воздействия приведут к дополнительным деформациям основания построенного сооружения. Например, строительство соседнего сооружения вызовет дополнительную местную нагрузку на основание р', которая приведет к развитию дополнительной неравномерной по длине построенного сооружения осадки s3 (рис. 9.1, г).
Эти рассуждения можно было бы продолжить. Но даже сейчас становится ясно, что полная деформация в некотором вертикальном сечении сооружения, отсчитываемая от проектного уровня подошвы фундамента, для рассматриваемого примера будет равна
s = – r + s1+s2 + s3, (9.1)
причем каждая составляющая этой деформации при известных значениях нагрузок на каждом этапе строительства и известных закономерностях деформирования грунта при его нагружении и разгрузке может быть определена.
Важно отметить, что приведенный пример сильно упрощает реальную обстановку строительства. Здесь не учитывались многие факторы, имеющие место в действительности и оказывающие влияние на деформации грунтов основания. К ним, прежде всего, относятся:
1) пространственная жесткость сооружения и возможность передачи различных нагрузок на основание через отдельные фундаменты;
2) неоднородность напластования и свойств грунтов в пределах пятна застройки;
3) скорость приложения нагрузок в процессе строительства и длительность развития осадок грунтов и т. п.
Все эти факторы приводят к значительному усложнению рассматриваемой картины, поэтому проблема прогноза деформаций оснований сооружений в целях инженерного проектирования основывается сейчас на ряде упрощающих предпосылок.
Под абсолютными перемещениями понимают осадку основания отдельного фундамента s и горизонтальное перемещение фундамента (или сооружения) и. К относительным перемещениям по СНиПу относят:
1) средние осадки основания сооружений,
2) относительную разность осадок двух фундаментов,
3) крен фундамента и т. п.
Относительные деформации могут быть найдены при определенных для различных фундаментов или сечений значениях абсолютных перемещений. Поэтому основные методы, рассматриваемые в настоящей лекции, посвящены определению величины абсолютных перемещений оснований отдельных фундаментов.
Расчет оснований фундаментов по деформациям в настоящее время производится исходя из условия
s ≤ su (9.2)
где s – совместная деформация (осадка, горизонтальное перемещение и т. п.) основания и фундамента (сооружения), определенная расчетом; su – предельное значение этой величины, устанавливаемое соответствующими нормативными документами или требованиями проекта.
Правила проектирования фундаментов сооружений в соответствии с условием (9.2) будут приведены в дисциплине «Основания и фундаменты». Здесь же рассматриваются лишь способы определения левой части этого неравенства.
Выше неоднократно отмечалось, что опытная зависимость между осадками поверхности грунтового основания и действующими нагрузками s –f(p) имеет нелинейный характер.
Однако в некотором интервале нагрузок, соответствующем фазе уплотнения грунта в основании, эта зависимость близка к линейной и развитие осадок во времени всегда имеет затухающий характер. В качестве максимального значения среднего давления р под подошвой фундамента, соответствующего границе фазы уплотнения, в настоящее время принимается расчетное сопротивление грунтов основания R. Это обосновывает возможность использования математического аппарата теории линейного деформирования грунтов для расчетов напряжений и деформаций основания при p≤R. Процесс строительства сооружения при этом рассматривается как одноразовое нагружение грунтов основания, вызывающее их общее деформирование без разделения на восстанавливающуюся и пластическую составляющие деформаций грунтов.
Несмотря на определенные недостатки, такой подход существенно упрощает математический аппарат расчетов деформаций. Оказывается возможным использовать теорию распределения напряжений в массиве грунтов, приведенную ранее, и деформационные характеристики грунтов.
Таким образом, одной из важнейших предпосылок рассмотренных в настоящей лекции методов расчета деформаций грунтов является ограничение среднего давления под подошвой фундамента условием p≤R.
Другой важной предпосылкой расчетов деформаций грунтов является введение понятий о стабилизированных и нестабилизированных (развивающихся во времени) перемещениях. Во многих случаях для инженерной практики представляют интерес только наибольшие (конечные, стабилизированные) перемещения, а время, в течение которого происходит стабилизация деформаций, не имеет существенного значения.
В то же время не всегда удается ограничиваться определением только конечных величин осадок. Поясним сказанное на примере. Пусть имеется сооружение (рис. 9.2, а),фундамент 1которого расположен на водонасыщенных глинистых, а фундамент 2— на песчаных грунтах. Пусть также характеристики деформационных свойств грунтов, действующие нагрузки и размеры фундаментов таковы, что конечные осадки s1 и s2 будут практически одинаковы и равны s∞ (рис. 8.2, б). Однако, поскольку время развития осадок водонасыщенных грунтов связано со скоростью фильтрации воды в грунте, а процессы фильтрации в глинистых грунтах протекают существенно медленнее, чем в песчаных, характер кривых s=f(t) для этих фундаментов будет совершенно различным. Может оказаться так, что осадка фундамента 2 стабилизируется
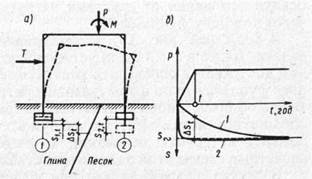
Рис. 9.2. Схема сооружения и развитие осадок разных фундаментов во времени
в течение срока строительства t, а осадка фундамента 1 к этому времени достигнет лишь некоторой доли конечной величины. Тогда к моменту окончания строительства разность осадок этих фундаментов Δst, может оказаться больше, чем предельная для данного типа сооружения величина Δsu. При этом сооружение может перестать соответствовать предъявленным к нему требованиям нормальной эксплуатации или даже претерпеть аварию, не достигнув времени стабилизации осадок обоих фундаментов.
В этом случае расчетом должен быть получен прогноз развития осадок каждого фундамента во времени и проведен анализ неравномерности деформаций сооружения для наиболее опасных периодов его строительства и эксплуатации. Такие расчеты выполняются в соответствии с теорией фильтрационной консолидации грунтов.
Наконец, может возникнуть и еще более сложная ситуация, когда требуется учесть поэтапность возведения сооружения. Простейший случай такой задачи был рассмотрен ранее (подъем дна котлована при его разработке и последующая осадка при строительстве сооружения). Может также понадобится определить осадку сооружения при p>R. Подобные задачи решаются с помощью нелинейной механики грунтов.
Теоретические основы расчета осадок оснований фундаментов
Постановка задачи. Рассмотрим наиболее простой случай взаимодействия фундамента неглубокого заложения с однородным грунтовым основанием. При глубине котлована менее 5 м деформациями разгрузки грунта ввиду их малости можно пренебречь. Ограничимся задачей определения конечной стабилизированной осадки основания от действия нагрузки, передаваемой на грунты через подошву фундамента.
Ранее было установлено, что для расчетов напряжений допускается определять контактные напряжения в уровне подошвы фундамента по формулам внецентренного сжатия. Полученная таким образом эпюра контактных напряжений рассматривалась как абсолютно гибкая местная нагрузка, заменяющая действие фундамента на грунты основания. С учетом сказанного характерные расчетные схемы этой задачи представлены на рис. 9.3.
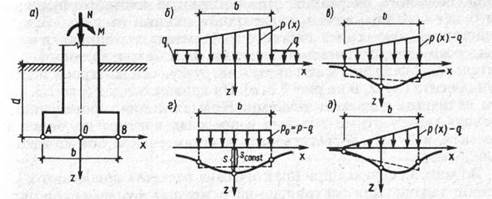
Рис. 9.3. Схема фундамента (а), расчетная схема передачи нагрузок на основание (б) и различные виды эпюр дополнительного давления (в – д)
В случае плоской задачи при внецентренном нагружении фундамента эпюра контактных напряжений будет иметь вид трапеции с переменной интенсивностью напряжений р(х). В стороны от подошвы фундамента будет действовать пригрузка, равная природному давлению на глубине заложения фундамента q = γd, где γ — удельный вес грунта (рис. 9.3, б). До строительства сооружения в любой точке основания существовуют напряжения, обусловленные весом вышележащей толщи. Будем считать, что грунты строительной площадки сформировались давно и их самоуплотнение под действием природного давления к периоду строительства завершилось. Тогда осадку поверхности основания в уровне подошвы фундамента будет вызывать уже не полное давление р(х), возникшее после строительства сооружения, а лишь приращение давления, равное p(x) – q. Назовем эту величину дополнительным вертикальным давлением на основание.
В зависимости от характера передачи нагрузок на фундамент могут различаться три разных вида эпюр дополнительного давления (рис. 9.3, в, г, д). Случаи в и д соответствуют внецентрен-ному, случай г – центральному нагружению фундамента. Очевидно, что и характер осадок основания в этих случаях будет различным.
Поскольку эпюра дополнительных давлений рассматривается как гибкая нагрузка, следует ожидать, что прогиб поверхности основания будет иметь криволинейное очертание (сплошные линии на рис. 9.3, в, г, д). В случае центрально-нагруженного фундамента кривая симметрична относительно оси z и максимальное значение прогиба будет совпадать с сечением, относящимся к этой оси. При внецентренном нагружении фундамента кривая имеет несимметричный характер и максимум прогиба смещен относительно оси z в сторону наибольшего значения p(x) – q.
Предположим, что мы умеем определять вид этих кривых для любого случая загружения. Однако, учитывая жесткость фундамента, действительный характер осадок поверхности не будет иметь криволинейного очертания. Для абсолютно жесткого фундамента он будет соответствовать пунктирным линиям на рис. 9.3, в,г, д. Действительную осадку жесткого фундамента можно найти с помощью следующего приема. Определим, рассматривая эпюру дополнительного давления как гибкую нагрузку, осадки краев и центра фундамента (А, О, Вна рис. 9.3, а).На кривых осадок (рис 9.3, в,г, д) эти величины показаны точками. Прямая линия, проведенная как средняя между этими точками в пределах контура подошвы фундамента, и будет соответствовать действительной осадке жесткого фундамента.
Во многих случаях при практических расчетах прибегают к упрощению задачи. Для центрально-нагруженных фундаментов определяется максимальная осадка s по оси z, которая и принимается как характерная величина совместной деформации основания и фундамента. Сопоставление значений s и осадки жесткого фундамента (рис. 9.3, г) позволяет заключить, что в этом случае имеет место некоторое завышение рассчитанной осадки на 21% для квадратного и на 16% для ленточного фундамента.
В случае внецентренно нагруженных фундаментов обычно определяется величина средней осадки и крена (тангенса угла наклона) подошвы фундамента.
Различают две группы методов расчета осадок: основанные на строгих решениях и дополнительных упрощающих предпосылках (приближенные решения).
Определение осадок линейно деформируемого полупространства или слоя грунта ограниченной мощности. В этом случае используются строгие решения о распределении напряжений в однородном изотропном массиве грунтов от нагрузок, приложенных на его поверхности. Зависимость между осадкой подошвы центрально-нагруженного фундамента s, площадью фундамента А = bl (b – ширина, l – длина подошвы фундамента) и средним значением дополнительного давления p0=p – γd(рис. 9.3, г) запишется в виде
s=ωpob(l-v2)/E,(9.3)
где ω– коэффициент, зависящий от формы площади и жесткости фундамента; Е, v — соответственно модуль деформации и коэффициент Пуассона грунта основания.
Значения коэффициентов ωбыли вычислены Ф. Шлейхером и Н. А. Цытовичем для полупространства, М. И. Горбуновым-Посадовым для слоя грунта ограниченной мощности h при различных соотношениях размеров подошвы фундамента п =l/b. Для разных расчетных случаев они приведены в табл. 9.1.
Таблица 9.1. Значения коэффициента ω
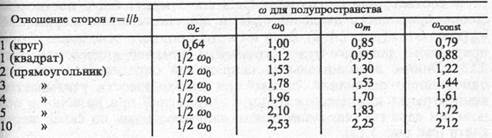
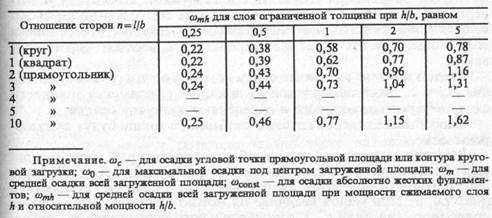
Деформационные характеристики грунта Е и v в формуле (9.3) определяются экспериментально. Значения коэффициента Пуассона могут также приниматься в зависимости от вида и физического состояния грунта. Так, для глин и суглинков твердой и полутвердой консистенции v изменяется от 0,1 до 0,15; тугопластичной — 0,2...0,25; пластичной и текучепластичной — 0,3...0,4; текучей — 0,45...0,5; для супесей — 0,15...0,3; для песков — 0,2...0,25.
Недостаток этого решения заключается в том, что оно применимо только для однородного напластования грунтов на значительную глубину ниже подошвы фундамента, что имеет место в относительно редких случаях. Кроме того, здесь не учитывается изменение природного напряженного состояния грунтов основания с глубиной, поэтому при значительных размерах фундаментов расчеты по формуле (9.3) дают завышенные значения осадок. Приведенное решение может быть использовано при небольших размерах фундаментов на однородных основаниях. В частности, оно применяется при решении обратной задачи — определении модуля деформации грунта по данным опытов с пробной нагрузкой.
Основные предпосылки приближенных методов определения осадок. Несмотря на то, что эти методы основаны на дополнительных упрощающих предпосылках, они обладают большей универсальностью, чем строгие решения, и используются в практических расчетах. Рассмотрим предпосылки приближенных методов на примере следующей задачи. Пусть требуется определить осадку s поверхности основания в уровне подошвы фундамента по оси z, проходящей через его центр тяжести, при действии равномерно распределенного дополнительного давления р0 (рис. 9.3, а).
Построем эпюры природного давления σzg(z) и дополнительных напряжений σzp(z) по оси z (рис. 9.4, а). В случае неоднородного основания эпюра природного давления будет ограничена ломаной линией. Эпюра дополнительных напряжений определяется как для однородного основания, однако при необходимости учитывается концентрация или деконцентрация напряжений при наличии в основании слоя грунта, существенно отличающегося по своей жесткости.
Отметим, что природное давление увеличивается, а дополнительные напряжения уменьшаются с глубиной. Поскольку уплотнение грунта и, как следствие этого, осадка его поверхности вызываются дополнительными напряжениями, очевидно, что основная доля общей осадки будет формироваться в верхней части основания.
Введем понятие глубины сжимаемой толщи грунтов основания Нс, т. е. такой измеряемой от подошвы фундамента мощности слоя, деформации которого и определяют величину осадки.
Способы нахождения глубины сжимаемой толщи будут рассмотрены ниже.
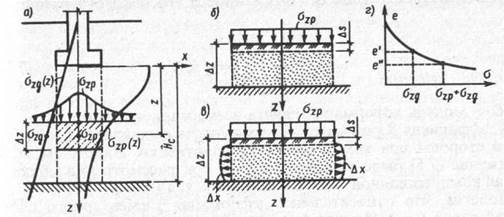
Рис. 9.4. Расчетные схемы к обоснованию приближенных методов определения осадок (а, б, в) и компрессионная кривая грунта (г)
Выделим в пределах сжимаемой толщи некоторый горизонтальный элементарный слой однородного грунта мощностью Δz, середина которого находится на глубине z от подошвы фундамента (рис. 9.4, а). При малой величине Δz можно полагать, что значения природного давления σzg и дополнительного напряжения σzp действующие по оси z, в пределах этого слоя постоянны и равны ординатам соответствующих эпюр в середине этого слоя. На горизонтальной поверхности слоя значения природного давления остаются постоянными, однако значения σzp уменьшаются по мере удаления от оси z.
Введем два дополнительных допущения. Предположим, что осадка основания происходит только за счет сжатия столба грунта, непосредственно находящегося под подошвой фундамента и ограниченного на рис. 9.4, а вертикальными пунктирными линиями. Это допущение приводит к преуменьшению рассчитываемой величины осадки, так как в действительности в основании деформируется значительно больший объем грунта, что подтверждается распространением изолиний напряжений в стороны от подошвы фундамента. Для того чтобы компенсировать этот недостаток, примем второе допущение. Будем считать, что сжатие каждого элементарного слоя вызывается равномерно распределенной на его поверхности нагрузкой, равной максимальному значению σzp, действующему по оси z. Это, в свою очередь, приведет к преувеличению сжатия каждого элементарного слоя, а следовательно, и общей осадки основания.
Если теперь определить величину сжатия каждого элементарного слоя в пределах сжимаемой толщи основания, а затем суммировать эти величины, то получим общую осадку основания фундамента.
Такой подход к решению задачи часто называют методом послойного (элементарного) суммирования.
Следовательно, общая задача сводится к определению величины сжатия элементарного слоя грунта под действием равномерной нагрузки на его поверхности. Здесь возможны два расчетных случая, на которых основаны различные методы определения осадок.
Сжатие элементарного слоя грунта без возможности его бокового расширения. Расчетная схема для этого случая представлена на рис. 9.4, б. Принимается, что сжатие элементарного слоя грунта происходит в условиях одномерной задачи (компрессионного уплотнения), т. е. εх=εу=0. Тогда из двух первых уравнений обобщенного закона Гука получим
σx = σy = σz ν (1 - ν ), (9.4)
где ν – коэффициент Пуассона грунта элементарного слоя.
Подставив это выражение в третье уравнение обобщенного закона Гука, получим после преобразований относительную деформацию элементарного слоя без возможности его бокового расширения:
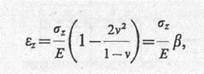 (9.5)
(9.5)
где Е — модуль деформации грунта элементарного слоя.
Коэффициент β учитывает невозможность расширения слоя грунта в стороны при компрессионном уплотнении.
Полагая, что относительная деформация элементарного слоя грунта равна εz=Δs/Δz, где Δs – величина его сжатия, а значение σz соответствует величине σzp, из уравнения (9.5) можно записать
Δs=σzphβ/E, (9.6)
или,
Δs=σzphmv, (9.7)
где mv=β/Е — относительный коэффициент сжимаемости грунта элементарного слоя; h=Δz.
Приведенная зависимость позволяет учесть нелинейный характер деформирования грунта в условиях компрессионного сжатия. Пусть имеется компрессионная кривая, полученная испытаниями образцов грунта, относящегося к рассматриваемому элементарному слою (рис. 9.4, г). Относительный коэффициент сжимаемости и модуль деформации грунта могут быть представлены в виде
mν=m0/(1+c'), Е=β(1+e')/m0 (9.8)
где e' — начальное значение коэффициента пористости грунта; m0 — коэффициент сжимаемости грунта, определяемый по формуле:
т0 = (e' – е")/(σ" – σ'),(9.9)
где, в свою очередь, σ', e' и σ", е" — сжимающее напряжение и коэффициент пористости грунта элементарного слоя соответственно до начала строительства и после стабилизации деформаций от построенного сооружения.
Поскольку до начала строительства в середине элементарного слоя действовало природное давление σzg, а после стабилизации осадок от построенного сооружения — полное напряжение, равное сумме природного давления и дополнительного напряжения σzg+σzp, то, отложив эти величины на оси σ компрессионной кривой, можно определить соответствующие им значения коэффициентов пористости e' и е". Тогда рассчитанный по формуле (9.9) коэффициент сжимаемости грунта и будет соответствовать тому изменению коэффициента пористости грунта, которое вызвано изменением сжимающего напряжения в рассматриваемом элементарном слое.
Подставив определенную таким образом величину т0 в формулы (9.8), можно с помощью формул (9.6) или (9.7) найти значение сжатия элементарного слоя грунта.
Сжатие элементарного слоя грунта с возможностью бокового расширения.В этом случае предполагается, что деформация элементарного слоя грунта происходит под действием всех компонент напряжений, возникающих в середине слоя по оси z от дополнительного давления р0. Нагрузка на поверхности слоя по-прежнему принимается равномерно распределенной и равной σzp. Однако теперь уже из-за действия горизонтальных сжимающих напряжений возможны деформации элементарного слоя и за пределы его боковых границ. Соответствующая расчетная схема представлена на рис. 9.4, в.
Тогда, используя обобщенный закон Гука и понятия модуля сдвига G и модуля объемной деформации грунта К, относительную деформацию элементарного слоя можно записать в виде
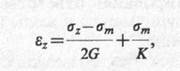 (9.10)
(9.10)
где G=E/[2(1 + v)];К=Е/(1 - 2ν);σт = (σх + σу + σz)/3.
В формуле (9.10) правая часть представлена как сумма деформаций изменения формы (первое слагаемое) и изменения объема грунта (второе слагаемое). Такая запись более точно отражает механизм деформирования грунта в пределах слоя. Так, если при ν =0,5 по условию предыдущей задачи [см. формулу (9.5)] εz=0, то здесь уже относительная деформация не будет равна нулю, так как первое слагаемое в выражении (9.10) не превращается в нуль. Иными словами, первое слагаемое правой части формулы (9.10) определит ту часть сжатия элементарного слоя, которая сформировалась за счет сдвиговых деформаций или бокового расширения грунта.
Окончательно сжатие элементарного слоя в случае пространственной задачи можно представить в виде
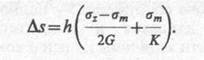 (9.11)
(9.11)
Для плоской задачи выражение (9.11) сохраняет вид, однако среднее напряжение будет определяться уже по формуле
σm=l/3((σx+σz)(l+ν). (9.12)
Следует обратить внимание на то, что компоненты напряжений σx σу, σz в приведенных выше формулах соответствуют тем величинам σxp σуp, σzp, которые рассчитаны для точки на оси z в середине элементарного слоя.
Так же как и в предыдущей задаче, для расчета осадок необходимо знать деформационные характеристики грунта элементарного слоя, в данном случае – модуль сдвига G и модуль объемной деформации К. В первом приближении они могут быть рассчитаны по приведенным выше формулам при известных значениях Е и ν. Однако более точное определение этих характеристик требует проведения специальных опытов в приборах трехосного сжатия.
Сопоставление рассмотренных расчетных случаев.Методы расчета осадок, учитывающие возможность бокового расширения грунта, в большей степени отражают действительное напряженное состояние основания и позволяют получать более точные результаты. Однако они более трудоемки и требуют проведения сложных экспериментальных исследований для определения деформационных характеристик грунтов основания. Поэтому эти методы обычно применяются при проектировании ответственных сооружений с большими нагрузками на фундаменты и жесткими требованиями к неравномерным деформациям.
Методы расчета осадок без возможности расширения грунта в стороны значительно проще. Для определения деформационных характеристик грунтов в этом случае используются стандартные компрессионные испытания. Для большинства промышленных и гражданских сооружений они позволяют получать достаточно точные значения прогнозируемых осадок. Поэтому в последующем основное внимание будет уделено методам, основанным на этой предпосылке.
Определение глубины сжимаемой толщи. В некоторых случаях мощность сжимаемой толщи грунтов непосредственно диктуется особенностями строения основания. Это имеет место тогда, когда при достаточно большой ширине фундамента на глубине от его подошвы порядка (2...3) b залегают прочные, практически не деформируемые грунты. Однако в большинстве случаев при отсутствии таких условий мощность сжимаемой толщи назначается на основе практических рекомендаций, отражающих опыт строительства.
В СНиП 2.02.01 - 83* «Основания зданий и сооружений» глубина сжимаемой толщи определяется из условия σzp(z) = 0,2σzg(z), т. е. нижняя граница сжимаемой толщи оснований промышленных и гражданских зданий и сооружений назначается на той глубине, где ордината эпюры дополнительных напряжений составляет 20% от природного давления на этой же глубине. Если же в пределах этой глубины залегают слабые грунты, характеризуемые модулем деформации Е<5 МПа, то мощность сжимаемой толщи увеличивается и ее нижняя граница назначается из условия σzp(z) = 0,1 σzg (z).
Имеются и другие предложения по определению глубины сжимаемой толщи грунтов основания. Так, ряд исследователей предлагают ограничивать сжимаемую толщу той глубиной, где ордината эпюры дополнительного давления будет равна σstr — структурной прочности грунта при компрессионном сжатии.
| <== предыдущая лекция | | | следующая лекция ==> |
| ВОДА И ЕЕ ПОДГОТОВКА. ТРЕБОВАНИЯ К ВОДЕ ДЛЯ ЛИКЕРО-ВОДОЧНОГО ПРОИЗВОДСТВА | | | Усилия в центробежных насосах. |
Дата добавления: 2020-02-05; просмотров: 1524;











