Частотно-модулированные сигналы

В генераторных измерительных схемах выходной сигнал яв­ляется частотно-модулированным. Если измеряемая величина изменяется по гармоническому закону, то выходное напряжение выражается соотношением (см. разд. 3.4.1)

,

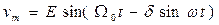где 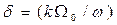m - коэффициент частотной модуляции. Спектр частот выходного сигнала можно определить, разлагая в ряд выражение для v_m:

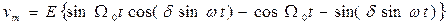
и вводя функцию Бесселя J_n(б) (рис. 3.31, а):

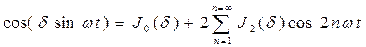
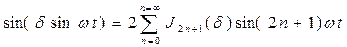
Тогда напряжение v_m можно записать в виде

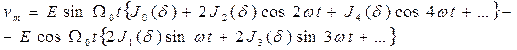
Элементарные тригонометрические преобразования позволяют выразить v_m в более простой форме:

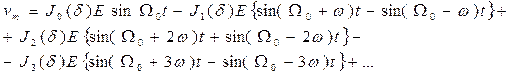
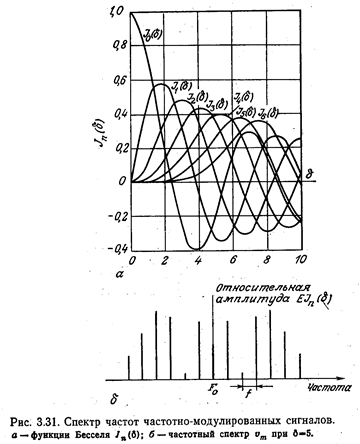
Таким образом, спектр выходного сигнала состоит из беско­нечного числа гармоник, симметрично распределенных по обе стороны от резонансной частоты F₀, отстоящих друг от друга на расстоянии f, с относительными значениями амплитуд 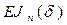(см. рис. 3.31, б).

Схемы обработки сигнала, имеющие ограниченную полосу пропускания, должны обеспечивать передачу спектра, достаточ­ного для неискаженного выделения информации. Амплитуды гармоник регулярно уменьшаются, начиная с определенного но­мера n гармоники, являющегося функцией δ. Оказывается, что δ+1 гармоник по одну и по другую сторону от частоты F₀ обеспечивают передачу около 98% энергии сигнала. Как следу­ет из правила Карсона, минимальная полоса пропускания, кото­рую должна иметь схема для обеспечения надлежащей передачи информации, определяется формулой

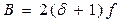
В случае δ<<1 требуемая полоса пропускания равна 2f.

Библиография

Монографии

1. Baurand J., Mesures electriques, Masson, Paris, 1961.

2. Fromy E, Mesures en radiotechnique, Dunod, Paris, 1953.

3. Marcus J., La modulation de frequence, Eyrolles, Paris, 1960.

4. Schwartz M, Information transmission, modulation and noise, McGraw, N.-Y., 1959.

5. Zuch E. L., Data acquisition and coversion handbook, Datel Intersil, Mans­field (U. S. A), 1979.