Ламинарное течение жидкости

<123 4 5 6 7 >

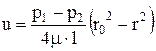
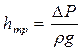
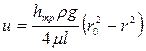
Используя значение скорости u, определим величину расхода через кольцевую площадь dω_c шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда

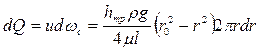Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r = r₀), получим

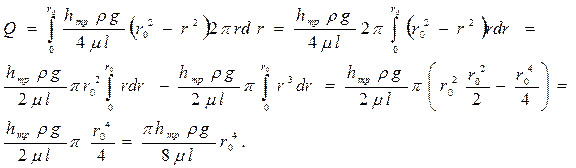
Средняя скорость в таком потоке будет

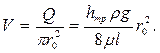
Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.

Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:

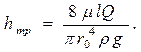
Заменив в этом выражении динамический коэффициент вязкости 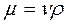кинематическим и выразив радиус трубы r₀ через диаметр d, получим

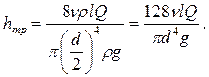
Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.

Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:

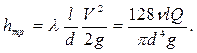
Заменим расход произведением 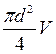и подставим в последнее равенство

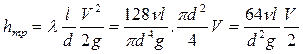Искусственно умножим и разделим числитель и знаменатель на V:

Очевидно, что в этом случае

.

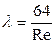Это выражение для коэффициента гидравлического трения при ламинарном движении жидкости хорошо подтверждается экспериментом и используется на практике для определения потерь энергии в потоке при ламинарном течении. Иногда этот коэффициент обозначается .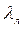

<123 4 5 6 7 >

Дата добавления: 2020-02-05; просмотров: 455;