Внезапное расширение.
В этом случае, одном из немногих, выражение для потери напора можно найти теоретическим путем.
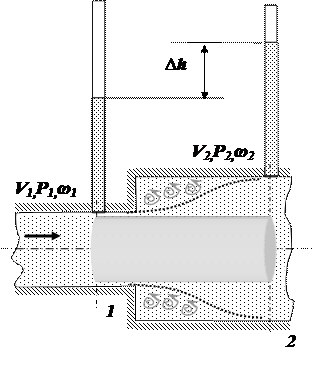 При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.
При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.
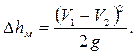
Назвав разность 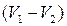 потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.
потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.
Последнюю формулу можно переписать в виде:
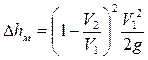 или
или 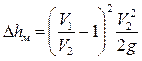 .
.
С учетом того, что на основании уравнения неразрывности потока 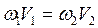 , те же потери напора можно представить в виде:
, те же потери напора можно представить в виде:
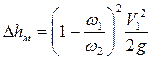 или
или 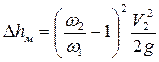 .
.
Сравнивая последние выражения с формулой Вейсбаха 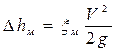 , можно выделить выражения для коэффициента местного сопротивления при внезапном расширении потока:
, можно выделить выражения для коэффициента местного сопротивления при внезапном расширении потока:
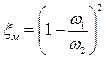 , если
, если 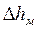 определять по скорости
определять по скорости 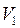 ;
;
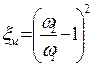 , если
, если 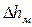 определять по скорости
определять по скорости 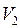 .
.
Дата добавления: 2020-02-05; просмотров: 810;











