Намагничивающая сила обмотки переменного тока
4.4.1 Намагничивающие силы обмоток.
При анализе н.с. обмоток примем следующие допущения:
1) насыщение стали отсутствует т.е. μст=∞;
2) воздушный зазор машины постоянный (отсутствуют пазы и явновыраженные полюса);
3) величина зазора δ мала по сравнению с Да.
Н.с. катушки с полным шагом.
Пусть на статоре машины переменного тока расположена одна катушка с числом витков Wк, с шагом у равным полюсному делению τ, по которой течет синусоидально изменяющийся ток iк= 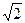 Iкsinωt. Этот ток создает магнитное поле, вид которого показан на рисунке.
Iкsinωt. Этот ток создает магнитное поле, вид которого показан на рисунке.
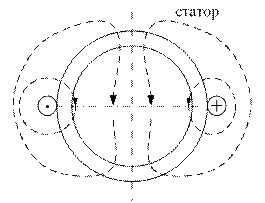
Рисунок 4.4.1 –Намагничивающая сила катушки с полным шагом
Применим к одной из силовых линий поля закон полного тока:
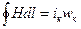 , ,
| (4.4.1) |
левая часть равенства будет иметь вид
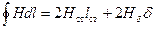 . .
| (4.4.2) |
Поскольку μст=∞, то Нст= В/ μст=0, и 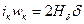
Магнитную индукция в зазоре можно определить как:
В = µ0Нδ= 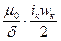 . .
| (4.4.3) |
Величину 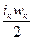 называют н.с. (или м.д.с.) катушки на один зазор Fkt, или В = λδ·Fkt, где
называют н.с. (или м.д.с.) катушки на один зазор Fkt, или В = λδ·Fkt, где
λδ=  - магнитная проводимость воздушного зазора.
- магнитная проводимость воздушного зазора.
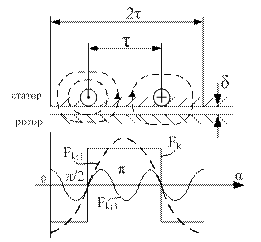
Рисунок 4.4.2 –Магнитное поле катушки с полным шагом
Уравнение (4.4.2) можно записать для любой силовой линии на одном полюсном делении, т.е. катушка создает прямоугольную волну н.с. (и В). Поскольку iк меняется во времени по синусоидальному закону, то высота волны н.с. так же изменяется во времени от Fkm= 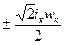 до 0.
до 0.
Прямоугольную волну н.с. можно разложить в пространстве в ряд Фурье
Fк = Fкt1cosα+ Fкt3cos3α+… +Fкtνcosνα+…
(косинусные члены, т.к. кривая симметрична относительно оси ординат, нечетные – т.к. симметричны относительно оси абсцисс)
Причем
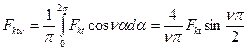 , (4.4.4)
, (4.4.4)
Следовательно
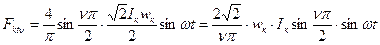 / (4/4/5)
/ (4/4/5)
а
Fk= 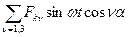 , ,
| (4.4.6) |
| Fk1=0,9Ik∙wk∙sinωt. | (4.4.7) |
Дальше будем рассматривать 1-ю гармонику н.с. (u, =>,B1)
Н.с. катушечной группы с полным шагом.
Рассмотрим катушечную группу в момент времени, когда Fk = Fкm, т.е. sinωt =1. Амплитуды н.с. катушек 1-х гармоник сдвинуты в пространстве на угол 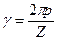 .
.

Рисунок 4.4.3 –Н.с. катушечной группы с полным шагом
Поэтому н.с. катушек можно изображать на пространственной векторной диаграмме

Рисунок 4.4.4 –Сложение н.с. катушек группы
| Fq1= qFk1kp1, | (4.4.8) |
где kp1 как и при расчете ЭДС находите по формуле
kp1= 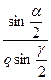
| (4.4.9) |
Для ν-й гармоники н.с. катушечной группы находится из выражения:
| Fqν=qFкν·kpν | (4.4.10) |
Н.с. фазы обмотки.
Рассмотрим двухслойную обмотку с укороченным шагом у=βτ. Такую обмотку можно пересоединить в две однослойные обмотки сдвинутые друг относительно друга на величину укорочения шага (1-β)τ. По этому вектора н.с. слоев в пространстве будут сдвинуты на тот же угол (1-β)π. Поэтому н.с. фазы можно найти по формуле: (амплитудное значение)
Fф1=2Fq1sin  =2Fq1cos(1-β) =2Fq1cos(1-β) 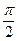 , ,
| (4.4.11) |
а для ν-ой гармоники
Fфν=2Fqνcosν(1-β) 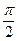 = 2Fqνsin = 2Fqνsin 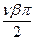 . .
| (4.4.12) |
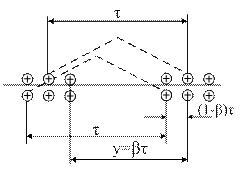
Рисунок 4.4.5 –Н.с. фазы обмотки с укороченным шагом

Рисунок 4.4.6 –Сложение н.с. двух слоев фазы обмотки
Если обозначить число последовательно соединенных витков фазы двухслойной обмотки как wф= 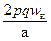 , ток катушки Iк=I/a, где I- ток фазы, а – число параллельных ветвей обмотки, то для амплитуды н.с. фазы ν-й гармоники получим выражение:
, ток катушки Iк=I/a, где I- ток фазы, а – число параллельных ветвей обмотки, то для амплитуды н.с. фазы ν-й гармоники получим выражение:
Fфν= 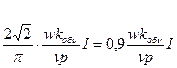 , ,
| (4.4.13) |
где kоб=kрν·kyν – обмоточный коэффициент ν-й гармоники.
Для мгновенного значения н.с. фазы справедливо выражение:
Fфt= 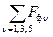 sinωt cosνα sinωt cosνα
| (4.4.14) |
Дата добавления: 2016-06-18; просмотров: 2688;











