Электропроводность металлов. Классическая электронная теория Друде-Лоренца
Металлы – хорошие проводники электрического тока.
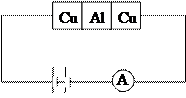 Носители заряда?
Носители заряда?
1) 1901 г. опыт Рикке
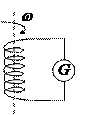 2) Инертные свойства
2) Инертные свойства
Томсон, Стюарт – качественно
Мандельштам, Папалекси – количественно
вращение – остановка!
Результат: носителями электрического тока в металлах являются свободные электроны.
Далее Друде и Лоренцом была создана классическая электронная теория электропроводности металлов.
В ней металлы представляли собой твердые вещества, в узлах которых находятся положительные ионы, совершающие непрерывные колебания у положения равновесия. А отрицательные электроны представляют собой практически свободные частицы – отрицательно заряженный электронный газ (в качестве модели использовалась модель идеального газа).
В отсутствие электрического поля электроны участвуют лишь в хаотическом движении с  , сталкиваясь лишь с узлами кристаллической решетки.
, сталкиваясь лишь с узлами кристаллической решетки.
В электрическом поле электроны приобретают направленное движение против поля и двигаются с ускорением:
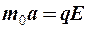
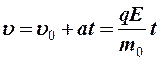
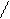 Но t ® ¥, т.к. происходит столкновение электронов с узлами кристаллической решетки.
Но t ® ¥, т.к. происходит столкновение электронов с узлами кристаллической решетки.

t - время между двумя последовательными
столкновениями;
 где
где  - средняя длина свободного пробега электронов º межузельное расстояние кристаллической решетки;
- средняя длина свободного пробега электронов º межузельное расстояние кристаллической решетки;
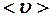 - средняя скорость теплового (хаотического) движения электронов.
- средняя скорость теплового (хаотического) движения электронов.
Вводя среднюю скорость дрейфа электронов по полю (среднюю скорость направленного движения) 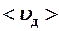
 ,
,
можно записать значение плотности электрического тока в проводнике
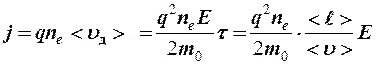 . (13-1)
. (13-1)
где 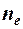 - концентрация электронов в проводнике;
- концентрация электронов в проводнике;
q - заряд электрона.
Сравнивая полученный результат с законом Ома для участка электрической цепи в дифференциальной форме
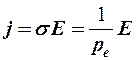 ,
,
можно записать выражение для удельной проводимости металлического проводника:
 . (13-2)
. (13-2)
Аналогичные рассуждения можно провести для теплового действия тока (закон Джоуля-Ленца).
Электроны, разгоняясь в электрическом поле, приобретают кинетическую энергию:
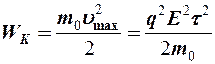 .
.
Тогда энергия всех электронов dN, приходящаяся на единицу объема dV металла за единицу времени свободного пробега приобретает значение

Сравнивая полученный результат с законом Джоуля-Ленца для участка электрической цепи в дифференциальной форме:
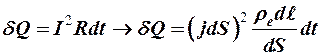 ,
,
 ,
,
(где 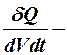 объемная плотность тепловой энергии, выделенная в металле в единицу времени при протекании электрического тока),
объемная плотность тепловой энергии, выделенная в металле в единицу времени при протекании электрического тока),
приходим к аналогичному результату (13-2)для удельной проводимости металлического проводника.
Полученный результат объясняет, почему разные металлы обладают разным электрическим сопротивлением.
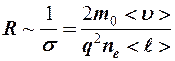 :
:
1) у разных металлов разная концентрация свободных электронов, которая определяется валентностью атомов a и концентрацией атомов nат:
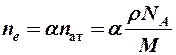 ,
,
где  - валентность атома;
- валентность атома;
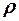 - плотность металла;
- плотность металла;
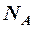 - постоянная Авогадро;
- постоянная Авогадро;
М - молярная масса металла;
2) у разных металлов разное строение кристаллической решетки:
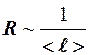 ;
;
3) средняя скорость теплового (хаотического) движения 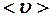 в разных металлах разная (даже при одинаковой температуре).
в разных металлах разная (даже при одинаковой температуре).
Полученный классической теорией результат объяснял температурную зависимость электрического сопротивления металла
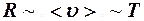 .
.
Более того, идея использовать модель идеального газа для описания тепловых свойств в твердых телах позволила Дюлонгу и Пти получить выражение для молярной теплоемкости твердых тел, которое хорошо удовлетворяло экспериментальным результатам в широком диапазоне температур:
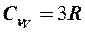 .
.
Однако, как раньше было рассмотрено, в области сверхнизких температур закон Дюлонга-Пти очень сильно расходился с экспериментом.
Более того, последовательное использование модели идеального газа приводила к результату, что молярная теплоемкость металлов должна была быть 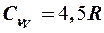 , что вообще противоречило эксперименту.
, что вообще противоречило эксперименту.
И, наконец, при изменении температуры металлического проводника его средняя скорость теплового (хаотического) движения меняется 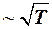
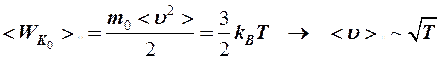 .
.
Значит, электрическое сопротивление R должно зависеть от абсолютной температуры Т металла согласно (13-2), как
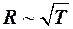
т. к.  ,
,  .
.
Но экспериментальные исследования зависимости 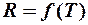 показывали, что эта зависимость в широком интервале температур линейная.
показывали, что эта зависимость в широком интервале температур линейная.

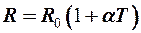 ,
,
где a = 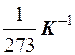 - температурный коэффициент сопротивления металла.
- температурный коэффициент сопротивления металла.
Объяснить эти противоречия с экспериментом классическая электронная теория не смогла.
Все ответы были получены лишь в рамках квантовой физики.
Дата добавления: 2020-02-05; просмотров: 529;











