Основные законы распределения случайных величин и их параметры.
1. Закон распределения случайной величины устанавливает соотношение между возможными значениями случайной величины Х и соответствующими им вероятностями. Закон распределения может быть задан в виде таблиц, формул, графически. Он дает полную информацию о свойствах случайной величины, позволяет оценить ее значение и определить вероятность нахождения ее значения в заданных границах.
Для дискретных и непрерывных случайных величин на практике часто применяют закон распределения в виде интегральной функции распределения F(x). Эта функция определяется вероятностью того, что случайная величина 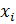 в i опыте примет значение, меньшее некоторого значения х:
в i опыте примет значение, меньшее некоторого значения х:
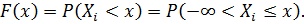
Интегральная функция распределения имеет следующие свойства - она неотрицательная, т.е. F(x) > 0; неубывающая, т.е. F( 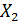 ) > F(
) > F( 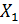 ), если
), если 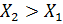 ; изменяется от 0 до 1, т.е. F(-
; изменяется от 0 до 1, т.е. F(- 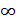 ) = 0, F(+
) = 0, F(+ 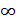 ) = 1.
) = 1.
Для описания распределения непрерывных случайных величин часто пользуются первой производной функции распределения 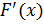 , которую называют плотностью распределения. Это связано с тем, что производную функции распределения
, которую называют плотностью распределения. Это связано с тем, что производную функции распределения 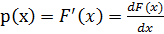 статистически (экспериментально) значительно проще определить, чем саму функцию распределения.
статистически (экспериментально) значительно проще определить, чем саму функцию распределения.
Плотность вероятности р(х) (дифференциальная функция распределения) определяется как предел отношения вероятности того, что случайная величина Х примет значение внутри бесконечно малого промежутка от х до х + dx к величине этого промежутка dx, когда dx 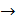 0:
0:
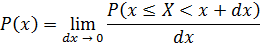
Функция распределения выражается через плотность вероятности:
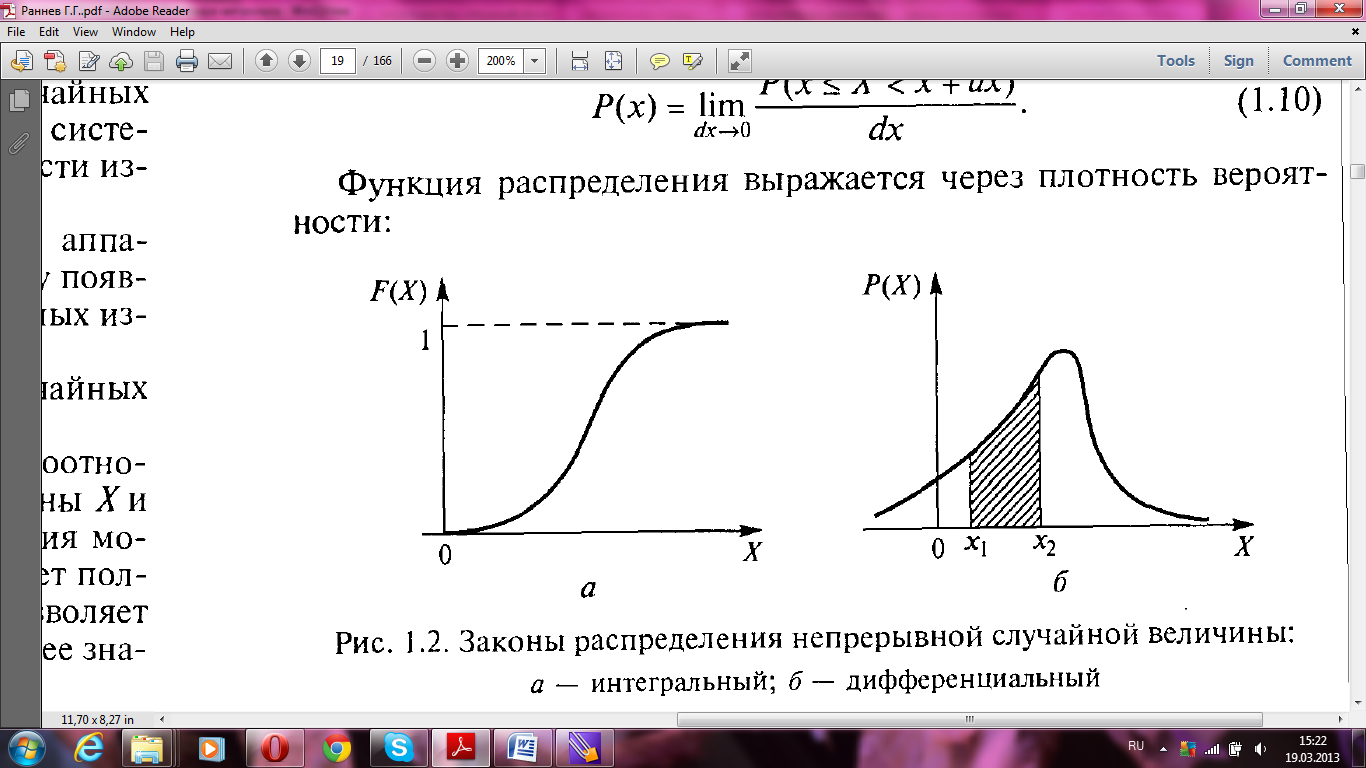
а) – интегральный; б) - дифференциальный
Рисунок - Законы распределения непрерывной случайной величины:
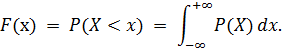
Вероятность попадания случайной величины в заданный интервал ( 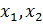 ) определяется как
) определяется как
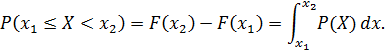
Графически эта вероятность равна площади криволинейной трапеции, ограниченной кривой распределения, осью абсцисс и прямыми Х = 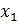 и Х =
и Х = 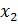 (рисунок б).
(рисунок б).
2. Математическое ожидание случайной величины (ее среднее значение) определяется как сумма произведений всех возможных значений дискретной случайной величины Х на вероятность этих значений Р:
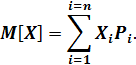
Для непрерывной случайной величины математическое ожидание
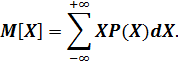
где Р(Х) - плотность распределения вероятностей случайной величины Х.
3. Дисперсия случайной величины Х - математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Для дискретной случайной величины дисперсия
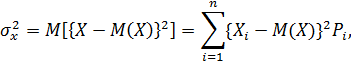
Для непрерывной случайной величины
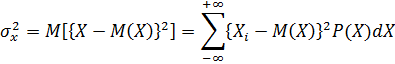
4. Среднеквадратичное отклонение случайной величины – корень квадратный из дисперсии:
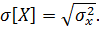
Дата добавления: 2016-05-28; просмотров: 3654;











