Преобразование и интеграл Фурье
Если функция 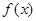 задана на всей числовой оси и не является периодической, то ее нельзя разложить в ряд Фурье, но можно представить интегралом Фурье.
задана на всей числовой оси и не является периодической, то ее нельзя разложить в ряд Фурье, но можно представить интегралом Фурье.
Если функция 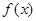 абсолютно интегрируема на всей числовой оси, т.е.
абсолютно интегрируема на всей числовой оси, т.е. 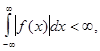 то говорят, что функция
то говорят, что функция 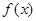 принадлежит к классу
принадлежит к классу 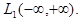
Теорема 1. Если 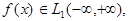 то при любом
то при любом 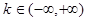 несобственный интеграл
несобственный интеграл
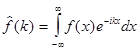 (1)
(1)
сходится, при этом функция 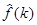 непрерывна при любом
непрерывна при любом 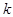 и
и 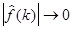 при
при 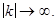
Доказательство.
Т.к. 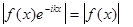
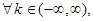 а интеграл
а интеграл 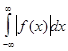 сходится, то согласно признаку Вейерштрасса (см. §1, гл.2), интеграл (1) сходится равномерно, а согласно теореме 2 §1, гл.2 функция
сходится, то согласно признаку Вейерштрасса (см. §1, гл.2), интеграл (1) сходится равномерно, а согласно теореме 2 §1, гл.2 функция 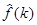 непрерывна. Вторую часть теоремы примем без доказательства.
непрерывна. Вторую часть теоремы примем без доказательства.
Теорема 2. Если 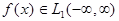 кусочно-непрерывная и имеет в каждой точке односторонние производные
кусочно-непрерывная и имеет в каждой точке односторонние производные 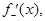
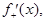 то в точках непрерывности функции
то в точках непрерывности функции 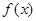 имеет место равенство
имеет место равенство
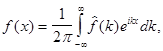 (2)
(2)
а в точках разрыва правая часть (2) равна полусумме пределов 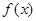 слева и справа (без доказательства).
слева и справа (без доказательства).
Замечание.Интеграл (2) сходится в смысле главного значения по Коши.
Равенства (1) и (2) называют соответственно прямым и обратным преобразованиями Фурье. Пишут 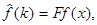
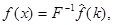
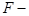 оператор Фурье.
оператор Фурье.
Преобразование Фурье аналогично преобразованию Лапласа и обладает аналогичными свойствами. В частности, согласно теореме 2 §1, гл.2.
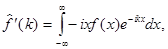 т.е. если
т.е. если 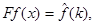 то
то 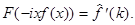 Это свойство аналогично свойству дифференцирования изображения по Лапласу. Можно доказать, что если
Это свойство аналогично свойству дифференцирования изображения по Лапласу. Можно доказать, что если 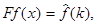 то
то 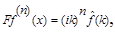 если
если 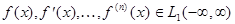 и
и 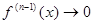 при
при 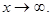
Если 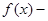 функция четная, то
функция четная, то
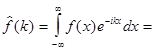
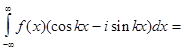
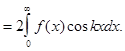 (3)
(3)
Из (3) видно, что 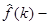 функция четная. Тогда
функция четная. Тогда 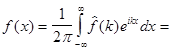
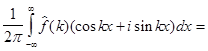
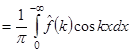 (4)
(4)
Итак, если 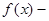 четная, то получаем косинус преобразования Фурье (3,4).
четная, то получаем косинус преобразования Фурье (3,4).
Аналогично, если 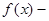 функция нечетная, получим синус-преобразование Фурье
функция нечетная, получим синус-преобразование Фурье
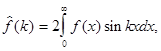 (5)
(5)
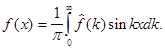 (6)
(6)
Подставим (1) в (2), получим
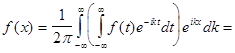
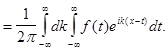 (7)
(7)
Формула (7) называется интегралом Фурье функции 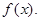 Ее можно записать в действительной форме
Ее можно записать в действительной форме
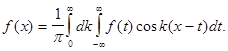 (8)
(8)
Сравним прямое и обратное преобразования Фурье (1,2) с рядом Фурье в комплексной форме:
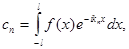 (9)
(9)
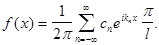 (10)
(10)
(Ради удобства множитель 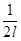 поставлен в формулу ряда Фурье, а не в формулу коэффициентов ряда Фурье). Частоты
поставлен в формулу ряда Фурье, а не в формулу коэффициентов ряда Фурье). Частоты 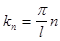 периодической функции
периодической функции 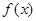 образуют арифметическую прогрессию
образуют арифметическую прогрессию 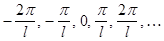 с разностью
с разностью 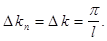 При неограниченном увеличении
При неограниченном увеличении 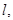 т.е. при
т.е. при 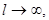
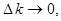 дискретный спектр становится непрерывным, а функция
дискретный спектр становится непрерывным, а функция 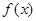 не периодической. При
не периодической. При 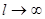 из (9) получим (1), а из (10) получим (2), т.е. вместо суммирования по дискретным частотам перейдем к интегрированию по параметру
из (9) получим (1), а из (10) получим (2), т.е. вместо суммирования по дискретным частотам перейдем к интегрированию по параметру 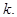 Поэтому функцию
Поэтому функцию 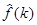 называют спектральной функцией (характеристикой), а
называют спектральной функцией (характеристикой), а 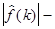 спектром функции
спектром функции 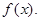 Этот спектр, согласно теореме 1, непрерывный.
Этот спектр, согласно теореме 1, непрерывный.
Пример.Представить интегралом Фурье функцию
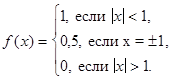
Решение.Найдем спектральную функцию
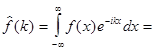
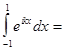
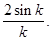 (11)
(11)
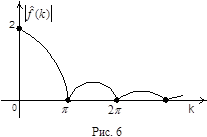
|
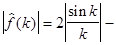 спектр данной функции
спектр данной функции
(см. рис. 6).
Подставляя (11) в (2), получим интеграл Фурье
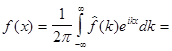
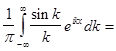
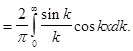 (12)
(12)
Дата добавления: 2020-02-05; просмотров: 260;










