Непрерывность функции. Классификация точек разрыва
Пусть функция 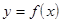 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Определение 1. Функция 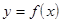 называется непрерывной в точке
называется непрерывной в точке  , если предел её в этой точке равен значению функции в этой точке, т.е. если
, если предел её в этой точке равен значению функции в этой точке, т.е. если
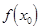 =
= 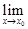
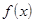 . (1)
. (1)
Пример 1. Покажем, что функция  =
= 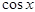 непрерывна в точке
непрерывна в точке  = 0. Действительно,
= 0. Действительно, 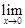
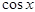 = 1 (см.пр.2 §3) и
= 1 (см.пр.2 §3) и 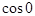 = 1, т.е. предел функции равен её значению. Согласно определению функция
= 1, т.е. предел функции равен её значению. Согласно определению функция  =
= 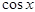 непрерывна в точке
непрерывна в точке
 = 0.
= 0.
Следствие 1. Если функция 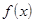 непрерывна в точке
непрерывна в точке  , то к пределу можно перейти под знаком функции, т.е.
, то к пределу можно перейти под знаком функции, т.е.
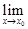
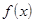 =
=  . (2)
. (2)
Действительно, поскольку  =
= 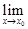
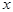 , то
, то 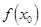 =
=  =
=
= 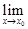
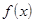 , т.к. функция непрерывна. Следствие доказано.
, т.к. функция непрерывна. Следствие доказано.
Разность 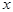 –
–  =
= 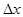 называют приращением аргумента, а разность
называют приращением аргумента, а разность 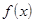 –
– 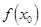 =
= 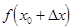 –
– 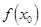 =
= 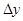 – приращением функции в точке
– приращением функции в точке 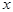 =
=  .
.
Следствие 2. Если функция непрерывна, то бесконечно малому приращению аргумента 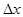 соответствует бесконечно малое приращение
соответствует бесконечно малое приращение 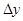 , т.е.
, т.е.
 = 0. (3)
= 0. (3)
Действительно, перепишем равенство (1) так:
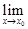
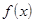 –
– 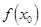 =0,
=0, 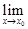 (
( 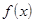 –
– 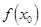 ) =
) = 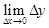 = 0. (4)
= 0. (4)
Следствие доказано.
Следствие 3. Если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.
Чтобы доказать это следствие, достаточно равенство (4) прочитать справа налево.
Если требования непрерывности функции в точке  не выполняются, т.е. функция не определена в точке
не выполняются, т.е. функция не определена в точке  или предел функции в точке
или предел функции в точке  не существует, или существует , но не равен значению функции в этой точке, то функция называется разрывной в точке
не существует, или существует , но не равен значению функции в этой точке, то функция называется разрывной в точке  , а сама точка
, а сама точка  называется точкой разрыва функции.
называется точкой разрыва функции.
Определение 2. Если функция непрерывна в каждой точке интервала (  ,
, 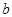 ), то она называется непрерывной на этом интервале. Если
), то она называется непрерывной на этом интервале. Если 
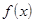 =
= 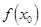 , то функция называется непрерывной в точке
, то функция называется непрерывной в точке  слева. Аналогично при
слева. Аналогично при 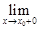
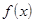 =
=
= 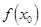 – непрерывной в точке
– непрерывной в точке  справа.
справа.
Определение 3. Если функция непрерывна в каждой точке интервала (  ,
, 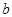 ),
),  <
< 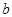 и в точке
и в точке 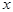 =
=  она непрерывна справа, а в точке
она непрерывна справа, а в точке 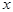 =
= 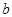 – слева, то она называется непрерывной на отрезке [
– слева, то она называется непрерывной на отрезке [  ,
, 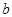 ].
].
Пример 2. Доказать, что функция  =
= 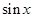 непрерывна в каждой точке своей области определения.
непрерывна в каждой точке своей области определения.
Доказательство. Пусть 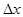 – приращение аргумента в произвольной точке
– приращение аргумента в произвольной точке  области определения функции. Тогда
области определения функции. Тогда
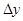 = sin (
= sin (  +
+ 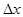 ) – sin
) – sin  = 2sin
= 2sin 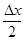 ×cos (
×cos (  +
+ 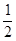
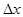 ).
).
Поскольку sin 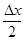 ® 0 при
® 0 при 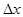 ® 0 (см. упражнение. в §3 гл.2), то и
® 0 (см. упражнение. в §3 гл.2), то и 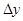 ® 0 при
® 0 при 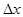 ® 0 (см. теорему 2 §4 гл.2). Тогда согласно следствию 3 функция
® 0 (см. теорему 2 §4 гл.2). Тогда согласно следствию 3 функция  =
= 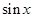 непрерывна в точке
непрерывна в точке  .
.
Что и требовалось доказать.
Аналогично можно доказать, что все основные элементарные функции непрерывны в своих областях определения. При этом, под основными элементарными функциями понимают следующие пять функций:
1) степенную  =
= 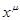 ,
, 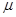 Î R;
Î R;
2) показательную  =
= 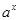 ,
,  > 0,
> 0,  ¹ 1;
¹ 1;
3) логарифмическую  =
= 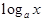 ,
, 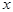 > 0,
> 0,  > 0,
> 0,  ¹ 1;
¹ 1;
4) тригонометрические  = sin
= sin 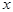 ,
,  = cos
= cos 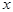 ;
;
5) обратные тригонометрические  = arcsin
= arcsin 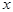 ,
, 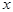 Î [ –1, 1],
Î [ –1, 1], 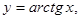
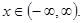
Пример 3. Исследовать на непрерывность функцию
 =
= 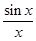 в точке
в точке  = 0.
= 0.
Решение. Поскольку точка  = 0 не входит в область определения этой функции, то она терпит разрыв в этой точке, не смотря на то, что имеет предел в этой точке.
= 0 не входит в область определения этой функции, то она терпит разрыв в этой точке, не смотря на то, что имеет предел в этой точке.
Пример 4. Исследовать на непрерывность функцию
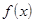 = sgn
= sgn 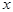 в точке
в точке  = 0.
= 0.
Решение. 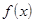 =sgn
=sgn 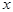 =
= 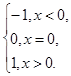 Очевидно,
Очевидно, 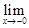
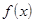 = –1,
= –1, 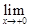
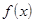 = +1, а
= +1, а 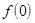 = 0. Поэтому эта функция разрывна в точке
= 0. Поэтому эта функция разрывна в точке  = 0.
= 0.
Пример 5. Исследовать на непрерывность функцию
 = sin
= sin 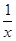 в точке
в точке  = 0.
= 0.
Решение. Т.к. функция не определена в точке  = 0 то она терпит в ней разрыв. Отметим, что эта функция не имеет предела в точке
= 0 то она терпит в ней разрыв. Отметим, что эта функция не имеет предела в точке  = 0 (см. пр.1 §3 гл.2).
= 0 (см. пр.1 §3 гл.2).
Пример 6. Исследовать на непрерывность функцию  =
= 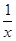 в точке
в точке  = 0.
= 0.
Решение. Поскольку функция не определена в точке
 = 0, то она разрывна в точке. Заметим, что
= 0, то она разрывна в точке. Заметим, что 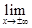
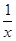 = ±¥.
= ±¥.
Пример 7. Исследовать на непрерывность функцию Дирихле
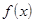 =
= 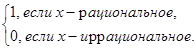
Решение. Функция определена в каждой точке числовой оси. Пусть  – произвольная точка числовой оси. Выберем две последовательности аргумента
– произвольная точка числовой оси. Выберем две последовательности аргумента 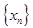 и
и 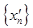 , сходящиеся к
, сходящиеся к  . Пусть члены первой последовательности рациональные числа, а второй иррациональные. Тогда соответствующие последовательности значений функции
. Пусть члены первой последовательности рациональные числа, а второй иррациональные. Тогда соответствующие последовательности значений функции 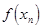 =1 и
=1 и 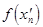 = 0 сходятся к единице и к нулю соответственно. А это означает, что данная функция не имеет предела. Данная функция разрывная в каждой точке числовой оси.
= 0 сходятся к единице и к нулю соответственно. А это означает, что данная функция не имеет предела. Данная функция разрывная в каждой точке числовой оси.
Определение 4. Если функция имеет предел в точке  , но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
, но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
Если функция имеет в точке  односторонние пределы, не равные между собой, то
односторонние пределы, не равные между собой, то  называется точкой разрыва первого рода. При этом
называется точкой разрыва первого рода. При этом 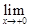
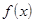 –
– 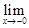
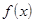 =
= 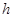 называется скачком функции в точке
называется скачком функции в точке  .
.
Если хотя бы один из односторонних пределов не существует или бесконечный в точке  , то эта точка разрыва второго рода.
, то эта точка разрыва второго рода.
Например, точка  в примере 3 является точкой устранимого разрыва, а в примере 4 – разрывом первого рода. Разрыв в примерах 5,6,7 второго рода.
в примере 3 является точкой устранимого разрыва, а в примере 4 – разрывом первого рода. Разрыв в примерах 5,6,7 второго рода.
Определение 5. Функция непрерывная на отрезке [  ,
, 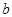 ] за исключением конечного числа точек этого отрезка, в которых она терпит разрывы первого рода, называется кусочно-непрерывной на этом отрезке. Функция называется кусочно-непрерывной на всей числовой оси, если она кусочно-непрерывна на любом отрезке этой оси.
] за исключением конечного числа точек этого отрезка, в которых она терпит разрывы первого рода, называется кусочно-непрерывной на этом отрезке. Функция называется кусочно-непрерывной на всей числовой оси, если она кусочно-непрерывна на любом отрезке этой оси.
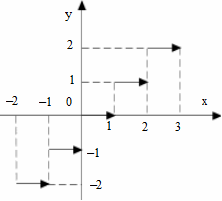
Пример 8. Исследовать на непрерывность функцию
 =
= 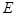 (
( 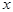 ), целую часть величины
), целую часть величины 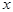 .
.
|
Решение. Очевидно, функция терпит разрывы при 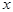 Î Z. В остальных точках она непрерывная. При этом
Î Z. В остальных точках она непрерывная. При этом 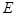 (0) = 0,
(0) = 0,
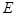 (± n) = ± n, n Î N,
(± n) = ± n, n Î N,
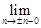
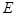 (
( 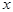 ) = ± n – 1 ¹
) = ± n – 1 ¹
¹ 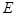 (± n),
(± n),
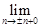
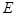 (
( 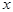 ) = ± n =
) = ± n =
= 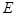 (± n).
(± n).
Таким образом, функция имеет точки разрыва только первого рода, в них она непрерывна справа. Это пример кусочно-непрерывной функции на всей числовой оси.
 § 8. Свойства непрерывных функций
§ 8. Свойства непрерывных функций
Теорема 1. Если функции 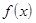 и
и 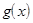 непрерывны в точке
непрерывны в точке 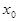 , то в этой точке непрерывны следующие функции:
, то в этой точке непрерывны следующие функции:
1) с  , с
, с 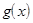 , с = const; 3)
, с = const; 3) 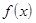 ×
× 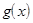 ;
;
2) 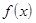 ±
± 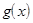 ; 4)
; 4) 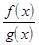 ,
, 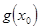 ¹ 0.
¹ 0.
Доказательство. Докажем третье утверждение теоремы. Поскольку предел произведения равен произведению пределов, то
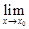 (
( 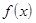 ×
× 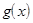 ) =
) = 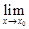
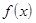 ×
× 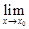
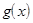 =
= 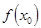 ×
× 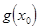 . (1)
. (1)
Равенство (1) и означает непрерывность функции 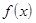 ×
× 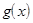 . Остальные утверждения доказываются аналогично.
. Остальные утверждения доказываются аналогично.
Рассмотрим две функции  =
= 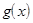 и
и 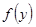 . Сложная функция
. Сложная функция 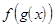 называется суперпозицией данных функций. Например,
называется суперпозицией данных функций. Например,  =
= 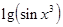 – суперпозиция трех функций: логарифмической, тригонометрической и степенной.
– суперпозиция трех функций: логарифмической, тригонометрической и степенной.
Теорема 2. Если функция  =
= 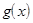 непрерывна в точке
непрерывна в точке 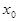 , а функция
, а функция 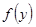 непрерывна в точке
непрерывна в точке 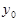 =
= 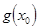 ,то сложная функция
,то сложная функция 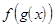 непрерывна в точке
непрерывна в точке 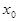 .
.
Доказательство. Поскольку функция  =
= 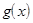 непрерывна, то
непрерывна, то
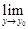
 =
= 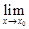
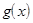 =
= 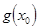 .
.
Используя первое следствие §7, получим
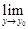
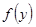 =
= 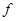 (
( 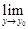
 ) =
) = 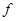 (
( 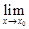
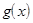 ) =
) = 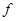 (
( 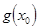 ).
).
Последнее равенство можно переписать так:
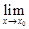
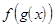 =
= 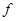 (
( 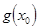 ). (2)
). (2)
Равенство (2) и означает непрерывность сложной функции в точке 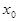 .
.
Замечание. Теорема 2 даёт правило замены переменных при вычислении пределов непрерывных функций
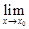
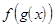 =
= 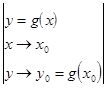 =
= 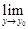
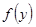 . (3)
. (3)
Теорема 3. Если функция  =
= 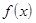 непрерывна в точке
непрерывна в точке 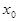 и
и 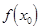 ¹ 0, то существует окрестность
¹ 0, то существует окрестность 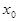 , в которой функция
, в которой функция 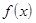 сохраняет свой знак (без доказательства).
сохраняет свой знак (без доказательства).
Функцию называют элементарной, если она получается путём конечного числа арифметических операций и суперпозиций пяти основных элементарных функций. Например,  =
= 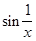 ,
,  =
=  – элементарные функции, а функции
– элементарные функции, а функции  = sgn x,
= sgn x,  =
= 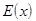 ,
,  =
= 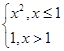 не являются элементарными. Функция Дирихле также неэлементарная.
не являются элементарными. Функция Дирихле также неэлементарная.
Поскольку все пять основных элементарных функций являются непрерывными в своих областях определения, то из теорем 1,2 вытекает следующее следствие: всякая элементарная функция непрерывна в своей области определения. Заметим, что для неэлементарных функций это утверждение не справедливо.
Теорема 4. Всякая непрерывная на отрезке [  ,
, 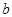 ] функция
] функция 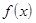 ограничена этом отрезке, достигает на нём своих наибольшего и наименьшего значений M = sup
ограничена этом отрезке, достигает на нём своих наибольшего и наименьшего значений M = sup 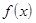 , m = inf
, m = inf 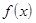 и принимает на нём все промежуточные значения из отрезка [ m, M]. (Без доказательства).
и принимает на нём все промежуточные значения из отрезка [ m, M]. (Без доказательства).
Замечание. Для функции, непрерывной на интервале (  ,
, 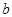 ), теорема 4 не справедлива. Например, функция
), теорема 4 не справедлива. Например, функция  =
= 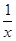 непрерывна на интервале (0,1), но не ограничена на нём и не достигает своих наибольшего и наименьшего значений.
непрерывна на интервале (0,1), но не ограничена на нём и не достигает своих наибольшего и наименьшего значений.
Следствие. Если непрерывная на отрезке [  ,
, 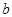 ] функция
] функция 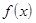 принимает на его концах значения разных знаков, то найдётся хотя бы одна точка
принимает на его концах значения разных знаков, то найдётся хотя бы одна точка 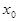 Î(
Î(  ,
, 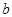 ), в которой функция обращается в нуль, т.е.
), в которой функция обращается в нуль, т.е. 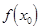 = 0. Доказательство очевидно.
= 0. Доказательство очевидно.
Следствие теоремы 4 часто используется для приближенного нахождения корней уравнения.
Пример. Найти корень уравнения 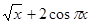 = 0.
= 0.
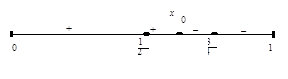
|
Решение. Рассмотрим функцию 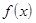 =
= 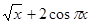 . Она элементарная, поэтому непрерывная для всех
. Она элементарная, поэтому непрерывная для всех 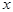 ³ 0.
³ 0.
Вычислим 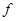 (0) = 2 и
(0) = 2 и 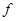 (1) = –1.
(1) = –1.
Т.к. значения функции разных знаков, то корень уравнения 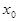 лежит в интервале (0,1), т.е. 0 <
лежит в интервале (0,1), т.е. 0 < 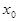 < 1. Разделим отрезок [0,1] пополам и вычислим
< 1. Разделим отрезок [0,1] пополам и вычислим 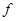
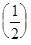 =
= 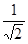 . Отсюда следует, что
. Отсюда следует, что 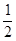 <
< 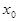 < 1. Разделим отрезок [1/2,1] пополам и вычислим
< 1. Разделим отрезок [1/2,1] пополам и вычислим 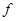
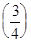 =
=
= 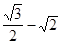 < 0. Отсюда следует, что
< 0. Отсюда следует, что 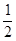 <
< 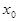 <
< 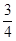 , т.е. мы уже вычислили корень уравнения с точностью до 0,25 . Продолжая этот процесс, можно вычислить корень с любой наперед заданной точностью.
, т.е. мы уже вычислили корень уравнения с точностью до 0,25 . Продолжая этот процесс, можно вычислить корень с любой наперед заданной точностью.
Дата добавления: 2020-02-05; просмотров: 738;











