Основные теоремы о пределах
Лемма. Для того, чтобы число  было пределом функции
было пределом функции 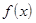 в точке
в точке  =
=  , необходимо и достаточно, чтобы разность
, необходимо и достаточно, чтобы разность 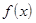 –
–  была бесконечно малой в этой точке.
была бесконечно малой в этой точке.
Доказательство. Обозначим разность 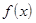 –
–  через
через 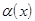 , т.е.
, т.е. 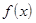 –
–  =
= 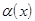 . Если
. Если  – предел функции
– предел функции 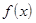 , то |
, то | 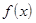 –
–  | = |
| = | 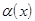 | <
| <  "
"  Î O (
Î O (  ,
, 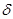 ). Но это означает, что
). Но это означает, что 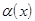 является бесконечно малой в точке
является бесконечно малой в точке  =
=  . Необходимость доказана. Если
. Необходимость доказана. Если 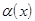 – бесконечно малая, то
– бесконечно малая, то
| 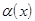 | = |
| = | 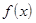 –
–  | <
| <  "
"  Î O (
Î O (  ,
, 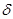 ). Последняя запись означает, что
). Последняя запись означает, что  является пределом функции
является пределом функции 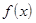 в точке
в точке  =
=  . Достаточность доказана.
. Достаточность доказана.
Теорема 1. Пусть функции 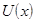 и
и 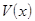 определены в некоторой
определены в некоторой 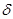 -окрестности точки
-окрестности точки  =
=  за исключением, быть может, самой точки
за исключением, быть может, самой точки  =
=  . Если существуют пределы функций
. Если существуют пределы функций 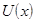 и
и 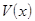 в точке
в точке  =
=  , то существуют и следующие пределы:
, то существуют и следующие пределы:
1) 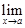 (
( 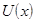 +
+ 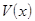 ) =
) = 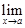
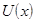 +
+ 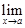
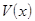 ,
,
2) 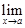 (
( 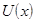 ×
× 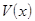 ) =
) = 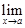
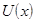 ×
× 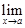
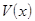 ,
,
3) 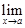
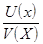 =
= 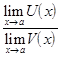 , если
, если 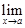
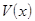 ¹ 0.
¹ 0.
Доказательство. Пусть 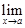
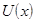 =
= 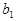 ,
, 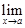
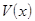 =
= 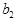 . Тогда согласно лемме
. Тогда согласно лемме
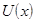 =
= 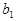 +
+ 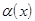 ,
, 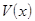 =
= 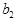 +
+ 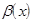 . (1)
. (1)
Учитывая (1), запишем 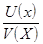 =
= 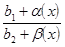 =
= 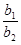 +
+
+ 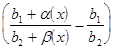 =
= 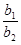 +
+ 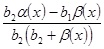 , или
, или
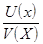 =
=  +
+ 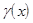 (2),
(2),
где 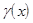 =
= 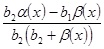 – бесконечно малая (согласно теоремам 1–3 предыдущего параграфа).
– бесконечно малая (согласно теоремам 1–3 предыдущего параграфа).
Равенство (2) согласно лемме означает, что
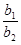 =
= 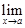
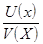 или
или 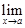
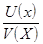 =
= 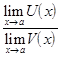 . Таким образом, третье утверждение теоремы доказано. Первое и второе утверждения доказываются аналогично. Доказать их самостоятельно.
. Таким образом, третье утверждение теоремы доказано. Первое и второе утверждения доказываются аналогично. Доказать их самостоятельно.
Из второго утверждения теоремы вытекает следующее следствие: если 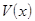 = C = const, то
= C = const, то 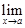 (C
(C 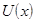 ) =
) =
= C 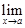
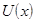 , т.е. постоянную можно выносить за знак предела.
, т.е. постоянную можно выносить за знак предела.
Теорема 1 значительно облегчает нахождение пределов.
Пример. Найти 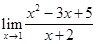 .
.
Решение. Используя теорему 1, запишем
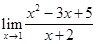 =
= 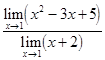 =
= 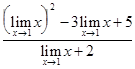 =
=
= 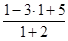 = 1.
= 1.
Теорема 2 (о двух милиционерах). Пусть функции 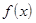 ,
, 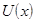 ,
, 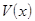 определены в некоторой
определены в некоторой 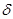 -окрестности точки
-окрестности точки  =
=  за исключением, быть может, самой точки
за исключением, быть может, самой точки  =
=  .
.
Если 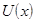 £
£ 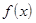 £
£ 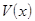 "
"  Î O (
Î O (  ,
, 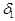 ) и
) и 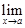
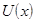 =
=
= 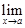
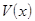 =
=  , то
, то 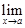
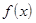 =
=  .
.
Доказательство. Согласно лемме 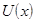 =
=  +
+ 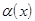 ,
, 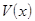 = =
= =  +
+ 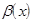 , где
, где 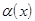 и
и 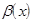 – бесконечно малые в точке
– бесконечно малые в точке
 =
=  , т.е. |
, т.е. | 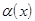 | <
| <  "
"  Î O (
Î O (  ,
, 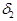 ) и |
) и | 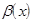 | <
| <  "
"  Î O (
Î O (  ,
, 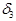 ). Данное в условии теоремы неравенство
). Данное в условии теоремы неравенство
 +
+ 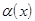 £
£ 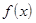 £
£  +
+ 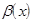 (3)
(3)
будет, очевидно, выполняться в наименьшей из трех окрестностей точки  =
=  , т.е. "
, т.е. "  Î O (
Î O (  ,
, 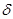 ),
), 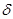 = min(
= min( 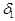 ,
, 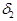 ,
, 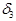 ).
).
Перепишем неравенство (3) так:
–  <
< 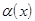 £
£ 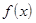 –
–  £
£ 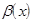 <
<  "
"  Î O (
Î O (  ,
, 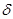 ), или
), или
| 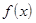 –
–  | <
| <  "
"  Î O (
Î O (  ,
, 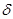 ).
).
Последнее неравенство означает, что  =
= 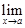
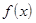 . Теорема доказана.
. Теорема доказана.
Теорема 3(правило замены переменной). Если существует предел функции 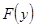 в точке
в точке 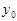 и существует предел функции
и существует предел функции 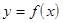 в точке
в точке 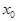 , причем
, причем 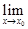
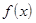 =
= 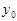 , то
, то 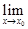
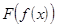 =
= 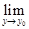
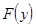 . (Без доказательства).
. (Без доказательства).
Дата добавления: 2020-02-05; просмотров: 410;











