при постоянном резервировании.

Анализ надежности системы при постоянном резервировании проведем при следующих допущениях:

1) для элементов справедлив экспоненциальный закон распределения;

2) показатели надежности устройств переключающих на резерв не учитываются;

3) изделия рассматриваются как невосстанавливаемые.

Тогда вероятность отказа системы с постоянным резервом и с целой кратностью равна:

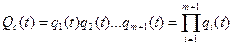
где q_i – вероятность отказа элемента системы, m – кратность резервирования.

Так как P_c(t) = 1 – Q_c(t), то вероятность безотказной работы равна:

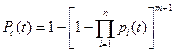
где p_i - вероятность безотказной работы элемента системы.

При экспоненциальном законе надежности, когда :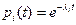

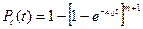
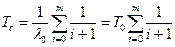
где - интенсивность отказов нерезервированной системы или любой из m резервных систем; Т₀ – среднее время безотказной работы нерезервированной системы или любой из m резервных систем.

Если резервированные объекты неравнонадежны, то

где q_i(t), p_i(t) – вероятность отказов и вероятность безотказной работы в течении времени t i-го объекта.

При общем резервировании замещением с целой кратностью, при экспоненциальном законе надежности и ненагруженном состоянии резерва:

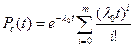
T_c = T₀(m+1)

где λ₀, Т₀ – интенсивность отказов и среднее время безотказной работы основного или нерезервированного объекта

При скользящем резервировании и экспоненциальном законе:

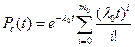
T_c = T₀(m₀+1)

где 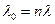- интенсивность отказов нерезервированной системы; λ – интенсивность отказов элемента; n – число элементов основной системы; T₀ - среднее время безотказной работы нерезервированной системы; m₀ – число резервных элементов.