Нормальное распределение случайной величины

Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

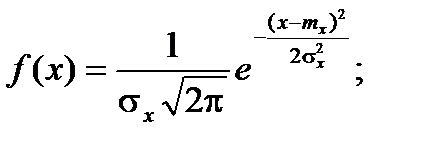
Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

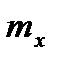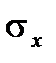Можно легко показать, что параметры и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.

Найдем функцию распределения F(x).

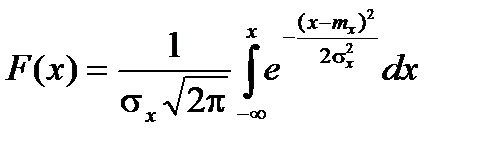
График плотности нормального распределения называется нормальной кривойили кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.

4) Найдем экстремум функции.

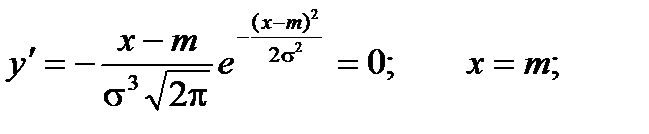
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный .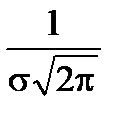

5) Функция является симметричной относительно прямой х = а, т.к. разность (х – а) входит в функцию плотности распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

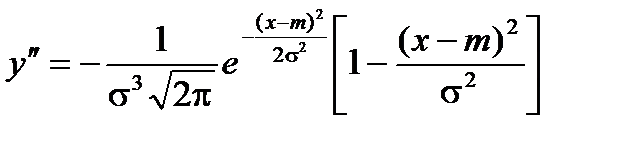
При x = m + s и x = m – s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно .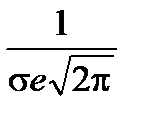

Построим график функции плотности распределения.

Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и s = 1 кривая называется нормированной.

Приложение 2.

Все функции Mathcad для интерполяции функциями

Встроенные функции категории Curve Fitting.

Таблица 1.

expfit(X,Y,vg)	Вычисляет коэффициенты экспоненциальной кривой ae^(bx) + c, наилучшим образом описывающей данные в X,Y. Вектор vg содержит начальные приближения искомых коэффициентов
genfit(X,Y, vg, F)	Вычисляет параметры заданной функции f , определенной в F и наилучшим образом описывающей данные в X,Y. Вектор vg содержит начальные приближения параметров. F – вектор–функция, первая компонента которой есть функция f, а остальные – частные производные f по искомым параметрам.
lgsfit(X,Y, vg)	Вычисляет коэффициенты логистической кривой a/(1+be^(–cx)), наилучшим образом описывающей данные в X,Y. Вектор vg содержит начальные приближения искомых коэффициентов
line(X,Y)	Вычисляет коэффициенты прямой ax + b, наилучшим образом описывающей данные в X,Y.
linfit(X,Y, F)	Вычисляет весовые коэффициенты линейной комбинации функций, заданных в F, наилучшим образом описывающей данные в X,Y. Значения в X должны быть отсортированы в возрастающем порядке.
lnfit(X,Y)	Вычисляет значения параметров для логарифмической кривой, наилучшим образом описывающей данные в X,Y. Вектор начальных приближений не нужен.
logfit(X,Y, vg)	Вычисляет коэффициенты логарифмической кривой a*ln(x + b) + c, наилучшим образом описывающей данные в ax + b. Вектор vgсодержит начальные приближения искомых коэффициентов
medfit(X,Y)	Вычисляет коэффициенты прямой вида ax + b, наилучшим образом описывающей данные в X,Y, методом медиан.
pwrfit(X,Y, vg)	Вычисляет коэффициенты степенной кривой вида ax*^b + c, наилучшим образом описывающей данные в X,Y. Вектор vgсодержит начальные приближения искомых коэффициентов
sinfit(X,Y, vg)	Вычисляет коэффициенты синусоидальной кривой a*sin(x + b) + c, наилучшим образом описывающей данные в X,Y. Вектор vgсодержит начальные приближения искомых коэффициентов

Из табл. 1 следует, что класс функций, которые можно применить для подбора наилучшего математического описания Y = f(X), весьма широк. Он варьируется от простейших линейных (line(vx, vy)) до произвольных функций (genfit(vx, vy, vg, F)) и линейной комбинации произвольных функций (linfit(vx, vy, F)).

В ряде задач, когда требуется полиномиальное описание данных может успешно использоваться часть встроенных функций категории Regression and Smoothing (регрессия и сглаживание) и функция interp(v,X,Y,x) из категории Interpolation and Prediction(интерполяция и прогноз),приведенные в табл. 2.

Встроенные функции категории Regression and Smoothing. Таблица 2.

slope (X,Y)	Вычисляет параметр a линии регрессии ax + b по данным X и Y
intercept(X,Y)	Вычисляет параметр b линии регрессии ax + b по данным X и Y
loess(X,Y,s)	Вычисляет вектор v, используемый функцией interp для нахождения совокупности полиномов второго порядка, наилучшим образом описывающих окрестности значений данных в массивах X и Y. Параметр s регулирует размер окрестности для локальной регрессии. Рекомендуемое значение s = 0.7–0.8
regress(X, Y, n)	Вычисляет вектор v для функции interp для нахождения коэффициентов полинома степени n, который наилучшим (в смысле наименьших квадратов) образом приближает данные Y в точках, определяемых X.
interp(v, X,Y, x)	Вычисляет интерполированные значения функции в точках x на основании предварительно найденного вектора коэффициентов v. Вектор v может быть получен одной из функций loess или regress на основе данных X и Y.