Краткие теоретические сведения Mathcad

Современный Mathcad располагает достаточно богатым ассортиментом встроенных средств (функций) для построения линейных и нелинейных зависимостей по экспериментальным данным. Сочетание этих средств со встроенной системой визуализации данных (построения разнообразных графиков) делает Mathcad удобным инструментом, позволяющим исследователю–экспериментатору быстро проводить обработку полученных эмпирических данных. При этом важно отметить, что всегда имеется возможность непосредственной реализации вычислений по формулам метода наименьших квадратов, и для линейной аппроксимации или для вычисления коэффициентов обобщенного полинома. Это особенно полезно для проверки корректности работы встроенных функций, которые выступают своего рода черными ящиками.

Определение коэффициентов линейного уравнения (линейная регрессия).Для решения задачи линейного регрессионного анализа, т.е. нахождения коэффициентов уравнения прямой 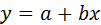используются две функции intercept и slope. Функция intercept (от англ. to intercept – отсекать) возвращает значение коэффициента а, а функция slope (англ. slope – наклон) – значение коэффициента b. Пример использования функций intercept и slope приведен рис. 4.3.

Рис.4.3Линейная регрессия с помощью функций intercept и slope.

Функции intercept и slope могут быть использованы также для определения параметров нелинейного уравнения регрессии. Для этого необходимо предварительно линеаризовать исходные данные. Необходимо так же отметить, что эта пара функций, по словам разработчиков Mathcad, оставлена для совместимости со старыми версиями. И при разработке новых программ в среде Mathcad лучше использовать функцию line(vx, vy), решающую ту же самую задачу, что и функции intercept и slope. В качестве результата функция line возвращает вектор, первый элемент которого – значение коэффициента а, в второй – значение коэффициента b, вычисленных по методу наименьших квадратов. Использование этой функции может выглядеть, например, так:

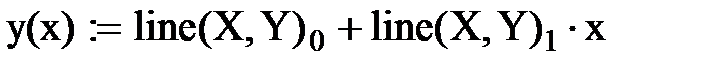
Помимо метода наименьших квадратов, рассчитать коэффициенты линейной регрессии можно с помощью другого, менее распространенного и известного алгоритма "средних медиан", или просто "медиан" (median–median regression). Для этого используют встроенную функцию medfit(x,y), где x и y — векторы координат точек экспериментальных данных.

Результатом ее работы является вектор, первой строке которого соответствует значение коэффициента а, а второй — коэффициента b уравнения регрессии.

Метод медиан очень прост:

1. Все экспериментальные точки надо разделить на три равные группы, исходя из величины x–координаты. В первой группе должны быть «левые» точки, во второй — «центральные», а в третьей — «правые». Если количество точек в выборке не кратно 3, то нужно действовать так, чтобы точки распределились по группам максимально равномерно. Если остаток от деления количества точек в выборке на три составляет один, то «лишнюю» точку следует поместить в центральную группу. Если «лишних» точек две, то по одной точке нужно прибавить в левую и правую группы.

2. Для каждой группы находится средняя точка, то есть точка, координаты которой являются средним арифметическим соответствующих координат всех точек группы.

3. Пишется уравнение прямой, проходящей через правую и левую средние точки.

4. Строится вторая прямая так, чтобы она была параллельна первой прямой. Располагаться вторая прямая должна между первой прямой и средней точкой центральной группы. Причем расстояние от второй прямой до первой должно быть в два раза меньше, чем от средней точки центральной группы до второй прямой. Смысл этого требования в том, что вторая прямая должна быть построена так, чтобы сумма расстояний от нее и до средних точек была минимальной. Параметры уравнения второй прямой возвращаются как результат.

Метод медиан довольно примитивен по сравнению с методом наименьших квадратов, и в большинстве случаев дает худший результат. Однако у метода медиан есть одно преимущество: он куда менее чувствителен к наличию в выборке промахов, то есть точек, полученных с недопустимо высокой погрешностью. Поэтому к нему нужно обращаться, если данные плохо ложатся на прямую.

Определение коэффициента парной корреляции.При проверке выбранной эмпирической формулы по методу выравнивания, близость линеаризованных данных к линейной зависимости часто определяется “на глаз”, что может оказаться весьма обманчивым (особенно при неудачно выбранном масштабе). В математической статистике определен специальный показатель, количественно характеризующий на сколько связь между парами точек 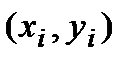близка к линейной. Это коэффициент парной корреляции:

.

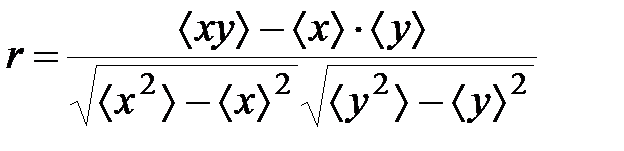Значения коэффициента парной корреляции всегда удовлетворяют соотношению 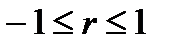. Чем меньше отличается абсолютная величина r от единицы, тем ближе связь между парами точек 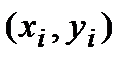к линейной. Если коэффициент парной корреляции равен нулю, то переменные X и Y называют некоррелированными.

Коэффициент парной корреляции используют, чтобы определить, существует ли между переменными линейная зависимость. Он показывает степень, в которой вариация одной переменной X связана с вариацией другой переменной Y, т.е. меру зависимости между переменными Х и Y.

Обсудим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов 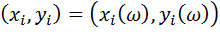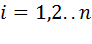. Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, называется число

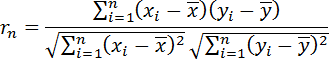
Если r_n = 1, то 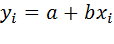причем a>0. Если же r_n = – 1, то 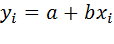причем a<0. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.

Коэффициент парной корреляции Пирсона может быть вычислен с помощью встроенной функции corr(vx, vy), где vx и vy – вектора, содержащие анализируемые данные.

Определение коэффициентов нелинейных зависимостей.Если в качестве эмпирической формулы выбрана одна из элементарных математических функций (экспоненциальная, логарифмическая и т.д.), то для определения ее параметров можно воспользоваться следующими функциями:

expfit(vx, vy, vg) –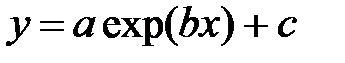

logfit(vx, vy, vg) –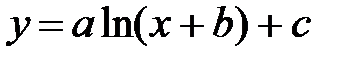

pwrfit(vx, vy, vg) –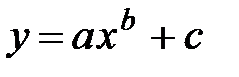

sinfit(vx, vy, vg) –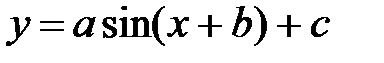

lgsfit(vx, vy, vg) –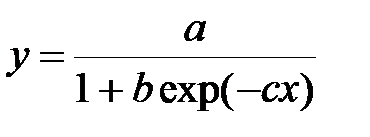

Каждая из этих функций имеет три параметра: vx, vy – вектора, содержащие анализируемые данные и вектор vg, элементам которого присваивают предполагаемые значения параметров a, b и с. В качестве результата функции возвращают вектор, содержащий рассчитанные значения коэффициентов a, b и с. Ниже, на рис.4.4., приведен пример использования функции expfit.

Рис.4.4 Пример использования функции expfit.

Для упрощения выбора функции в таблице приведены основные типы графиков вместе с математическим описанием и функцией Mathcad.

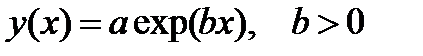
	expfit		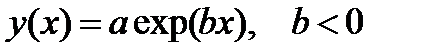expfit
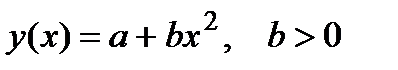
	pwrfit		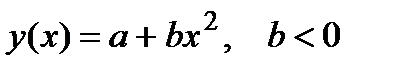pwrfit
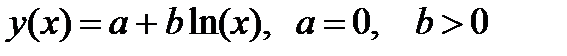
	logfit		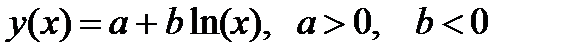logfit
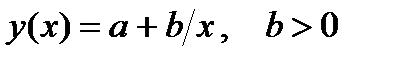
	pwrfit		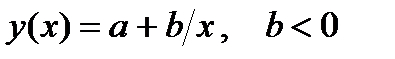pwrfit

Аппроксимация обобщенным многочленом. Часто аппроксимирующую функцию y(x) выбирают в виде линейной комбинации произвольных функций (обобщенного многочлена)

,

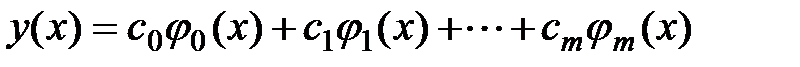где 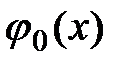, , 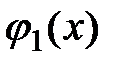…, 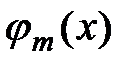– функции заданного вида (базисные функции). Задача аппроксимации сводится к нахождению коэффициентов разложения 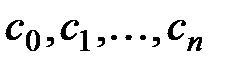. Напомним, что для нахождения этих коэффициентов в рамках метода наименьших квадратов необходимо решить систему линейных алгебраических уравнений с матрицей Грамма.

В пакете Mathcad задачу аппроксимации обобщенным многочленом решает функция linfit (vx, vy, F). Функция имеет три параметра: первые два vx и vy – вектора, содержащие исходные данные; третий параметр F – вектор, каждый элемент которого является базисной функцией. В качестве результата функция linfit возвращает вектор коэффициентов .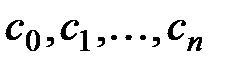

Пример использования функции linfit приведен на рис.4.5.

Рис.4.5 Пример использования функции linfit

Аппроксимация обобщенным многочленом нелинейного вида. Вообще при проведении регрессии общего вида, можно найти параметры зависимости совершенно любого вида. В Mathcad есть встроенная функция genfit(x,y,g,F), которая дает возможность справляться с этой задачей.

В качестве аргументов данная функция принимает следующие параметры:

x — вектор опытных данных по оси абсцисс;

y — эмпирические данные по оси ординат;

g — вектор приближений для неизвестных параметров. Правила его задания такие же, как при вычислении регрессии специального вида;

F(x, g) — вектор–функция из n+1 элемента, где n — количество рассчитываемых параметров. Первый элемент данной функции — это описывающая экспериментальную зависимость функция, параметры которой должны быть рассчитаны. Сами параметры должны фигурировать в выражении как соответствующие элементы вектора g. Следующие n элементов вектор–функции F должны быть заполнены выражениями частных производных описывающей зависимость функции поискомым параметрам. Последовательность частных производных должна быть такой же, как последовательность приближений к соответствующим им параметрам в векторе g.

Из всех встроенных функций регрессии genfit является наиболее универсальной, однако и наименее точной и трудной в использовании. Как и для всех остальных регрессий специального вида, огромное влияние на точность расчета неизвестных параметров с помощью функции genfit оказывает близость значений элементов вектора g к истинным их величинам. Кроме того, в отличие от всех остальных встроенных функций регрессии, точность результата вычислений с помощью genfit зависит от значения системной переменной TOL.

Далее, на рис.4.6, приведен пример расчета параметров эмпирической зависимости с помощью функции genfit.

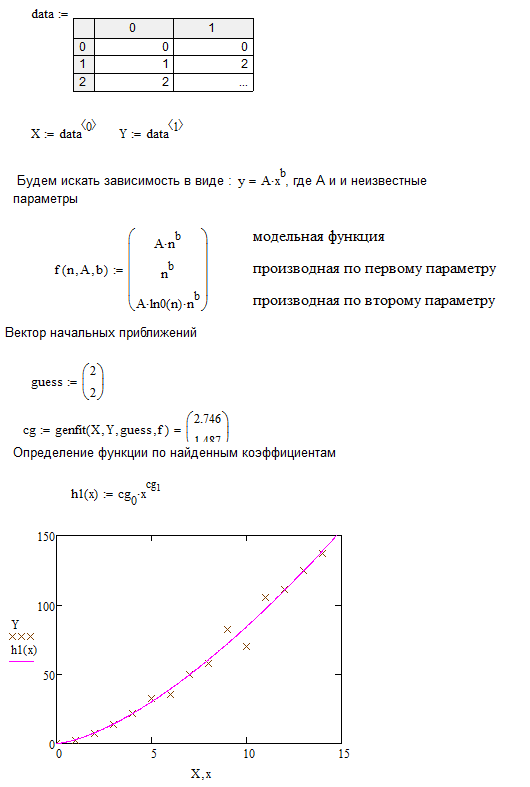
Рис.4.6 Пример использования функции genfit

Аппроксимация степенным многочленом. Для аппроксимации зависимостей степенным многочленом

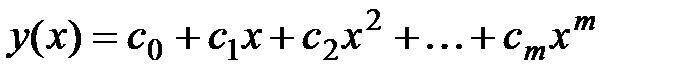
используется функция regress(vx, vy, m). Функция имеет три параметра: первые два vx и vy – вектора, содержащие исходные данные; третий параметр m – степень многочлена. В качестве результата функция regress возвращает вектор, в котором первые три элемента содержат некоторые значения, используемые функцией interp,которую мы рассматривали на прошлой лекции, а остальные – значения коэффициентов с_i. Вариант использования функции приведен на рис.4.7.

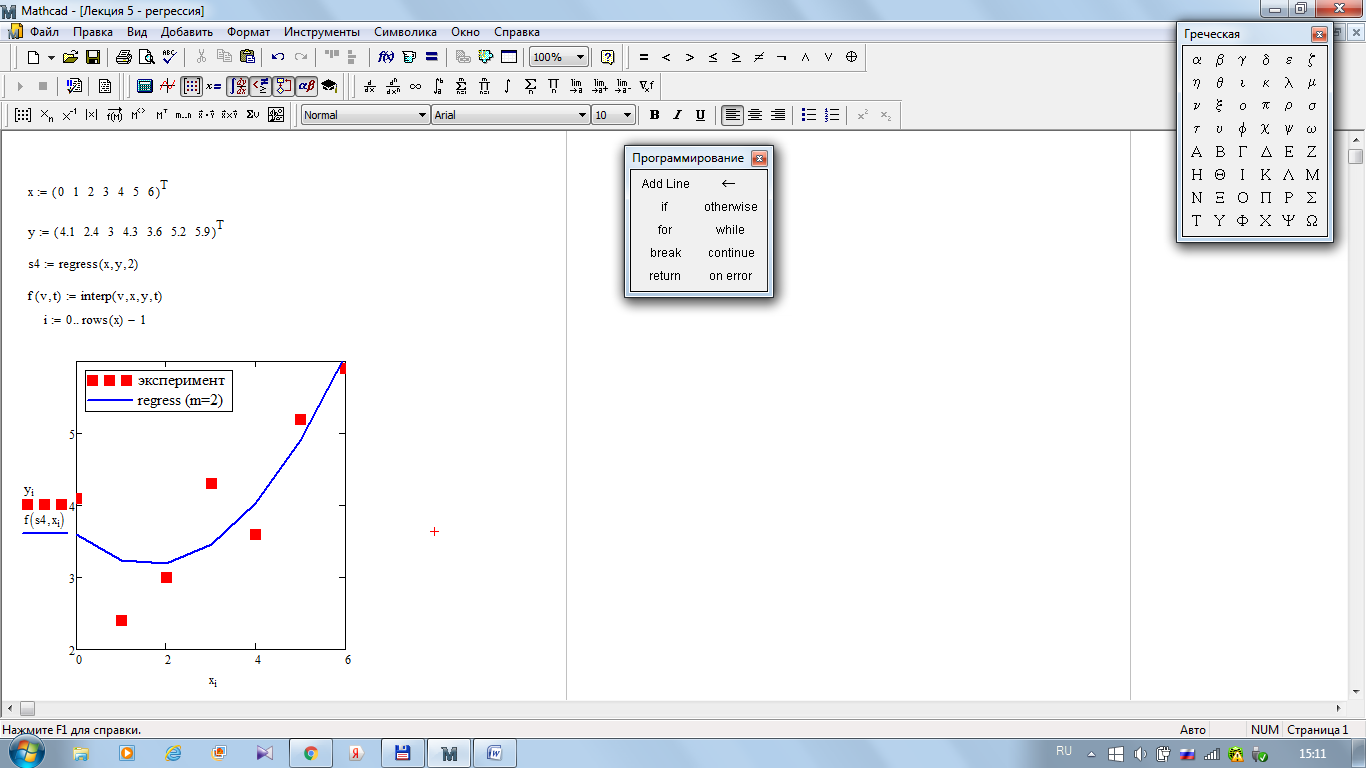Рис. 4.7 Применение функции regress

На рис. 4.7 приведен пример использования функции regressдля получения коэффициентов полинома третьей степени (выделен желтым фоном). Значения полинома размещены в векторе у для значений аргумента, которые содержатся в векторе х. Вектор случайных нормально распределенных чисел z имитирует наличие помех в измерениях. Результирующий вектор, по которому находится решение, обозначен через Y. Функция regressформирует вектор параметров D, первые два элемента которого имеют характер служебной информации, третий параметр – порядок полинома, а остальные параметры – коэффициенты полинома в порядке возрастания степеней, начиная со свободного члена. Функция interpвосстанавливает значения полинома по полученным коэффициентам. Исходный и восстановленный векторы значений полинома объединены в матрицу S. Приведены также вектор ошибок и норма этого вектора в качестве критерия точности полученных результатов. На графиках представлены исходные и восстановленные значения полинома, а также значения абсолютных ошибок. Полученные данные свидетельствуют о значительном влиянии помех на результирующие значения коэффициентов. Так, уже при среднеквадратическом отклонении помехи, принятом равным 0.1, имеем заметные искажения значений коэффициентов полинома (свободный член 0.986 вместо 1.0, коэффициент при старшей степени 0.108 вместо 0.1 и т.д.). Программа, приведенная на рис.4.7, может быть использована для анализа степени влияния случайных помех в измеренных данных на конечный результат.

Задача, аналогичная рассмотренной может быть решена традиционным методом наименьших квадратов, причем результаты при тех же исходных данных будут, естественно, практически совпадать .

Регрессия отрезками полиномов. Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress (см. рис.4.8):

· loess (х, у, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов;

· interp(s,x,y,t) — результат полиномиальной регрессии:

· s=loess(х,у,span);

· х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

· у — вектор действительных данных значений того же размера;

· span — параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).

Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).

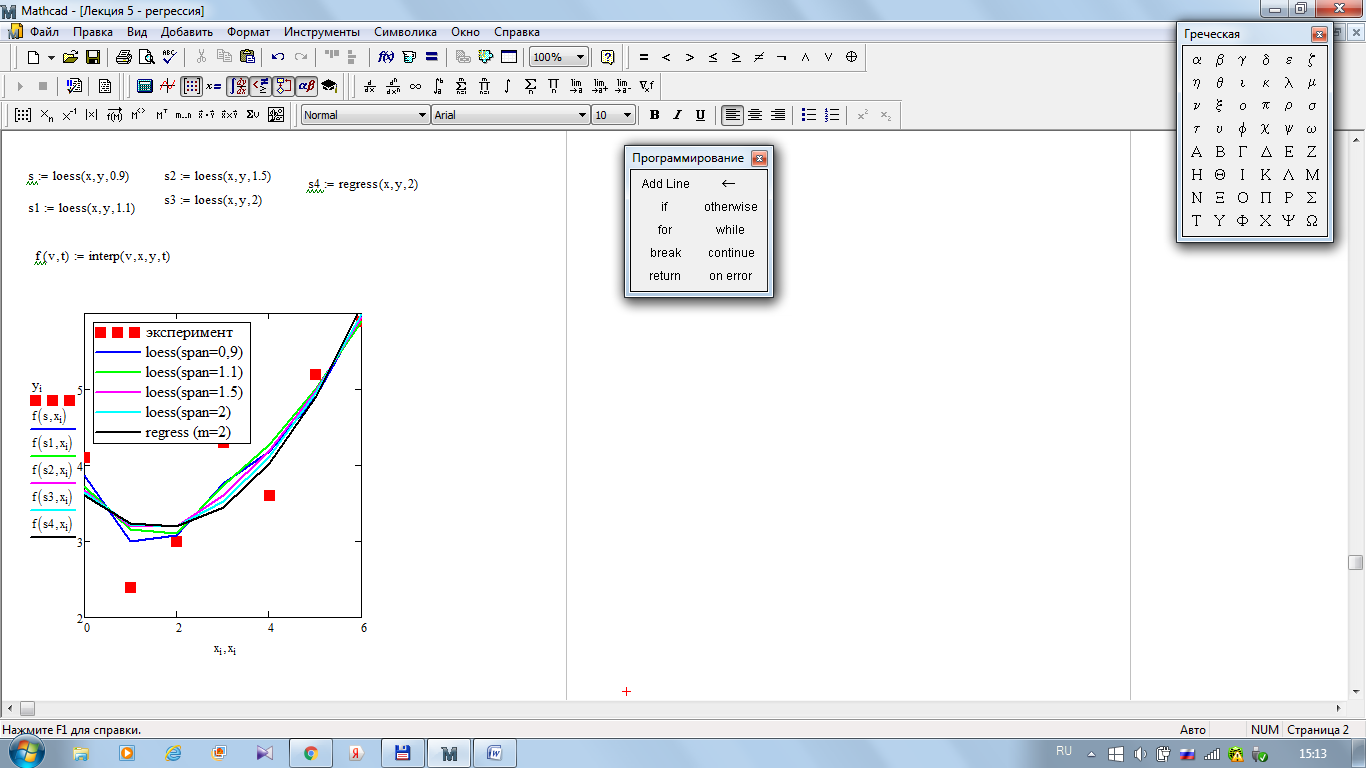Рис.4.8 Регрессия отрезками полиномов

Необходимо отметить, что на рис.4.8. функция f принимает два аргумента: один t – стандартный, для определения точки в которой надо рассчитать значение функции, а второй v – вектор с коэффициентами интерполяции. Такой способ задания функции (от двух аргументов) позволяет, используя одну функцию, строить на графике сразу несколько кривых, соответствующих различным значениям векторов, полученных с помощью loess.

Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.

Двумерная полиномиальная регрессия. По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией, Mathcad позволяет приблизить множество точек Z_i,j(x_i,y_j) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.

· regress (x,z,k) — вектор коэффициентов для построения полиномиальной регрессии данных.

· loess (x, z, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов.

· interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами.

· s — вектор вторых производных, созданный одной из сопутствующих функций loess или regress.

· х — матрица размерности Nx2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у).

· z — вектор действительных данных размерности N.

· span — параметр, определяющий размер отрезков полиномов.

· k — степень полинома регрессии (целое положительное число).

· v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.

Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, которая требует их представления в виде матрицы NxN). В связи с этим данные представляются как вектор.

Двумерная полиномиальная регрессия иллюстрируется на рис4.9. Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например, z, в качестве вектора, а не строки).

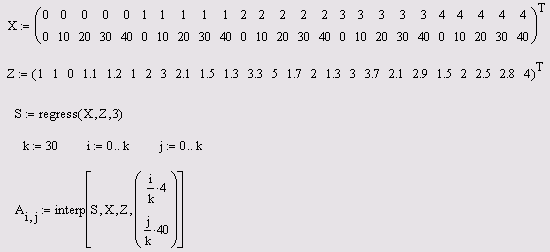
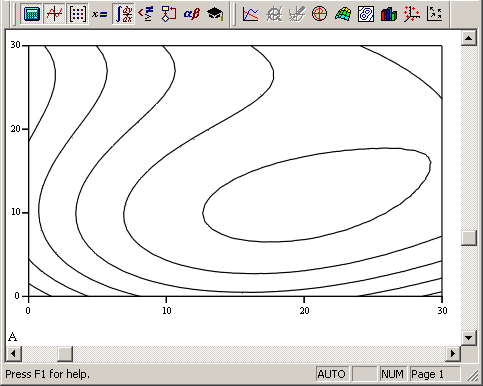Рис.4.9 Двумерная полиномиальная регрессия

Сглаживание экспериментальных данных.

Последняя задачей, которую можно отнести к задачам о нахождении аппроксимационной функции – это задача сглаживания экспериментальных данных. В пакете Mathcad для решения этого типа задач существуют три функции:

• medsmooth(VY,n)— для вектора с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);

• ksmooth(VX,VY, b) — возвращает n-мерный вектор сглаженныхVY,вычисленных на основе распределения Гаусса.VX и VY— n-мерные векторы действительных чисел. Параметр b (полоса пропускания) задает ширину окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );

• supsmooth(VX, VY) — возвращает n-мерный вектор сглаженныхVY, вычисленных на основе использования процедуры линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с адаптивным выбором k.VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания.

Пример использования этих функций приведен на рис. 4.10

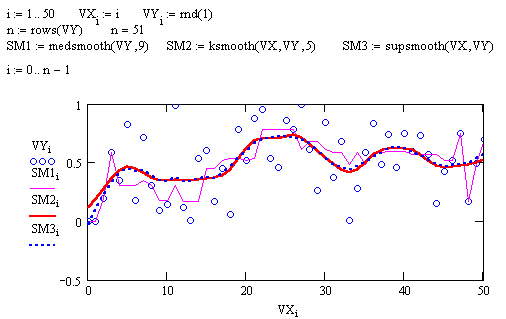Рис.4.10 Сглаживание экспериментальных данных

Приложение 1.