Критика теории Пиаже

Теория Пиаже — огромное интеллектуальное достижение; она произвела революцию в представлениях о когнитивном развитии детей и в течение десятилетий вдохновляла огромное количество исследователей. Наблюдения Пиаже относительно последовательности когнитивного развития подтверждаются многими исследованиями. Однако более новые и изощренные методы тестирования умственной деятельности младенцев и дошкольников показывают, что Пиаже недооценивал их способности. Как мы отмечали выше, для того чтобы ребенок мог успешно решить многие из задач, созданных для проверки теории стадий, ему на самом деле надо владеть несколькими базовыми навыками обработки информации: вниманием, памятью и знанием конкретных фактов. И может получиться так, что ребенок на самом деле обладает требуемой от него способностью, но не может решить задачу, потому что у него нет других навыков, также необходимых, но несущественных для данной задачи.

Эти моменты проявились со всей очевидностью в исследованиях постоянства объекта — осознания того, что объект продолжает существовать, даже когда он находится вне поля чувственного восприятия. Мы уже говорили выше, что если младенцу в возрасте до 8 месяцев показывают игрушку и затем у него на глазах прячут ее или накрывают тряпкой, он ведет себя так, как будто она уже не существует, не пытается ее искать. Но и после 8-месячного возраста ребенок, уже сумевший неоднократно отыскать игрушку, спрятанную в каком-то одном месте, продолжает искать ее там же, даже после того как видел, что взрослый спрятал ее в новом месте.

Заметьте, однако, что для успешного выполнения этого теста ребенку нужно не только понимать, что данный предмет все еще существует (т. е. знать о постоянстве объекта), но также помнить, куда его спрятали, и проявлять какое-то физическое действие, которое показывало бы, что он его ищет. Поскольку Пиаже считал, что раннее когнитивное развитие определяется сенсомоторной активностью, он не рассматривал всерьез возможность того, что ребенок знает, что объект все еще существует, но не способен выразить это в поисковом поведении, — т. е. что развитие ума может опережать моторные способности.

Такая возможность была изучена в ряде исследований, где от ребенка не требовалось активно искать спрятанный объект. Как показано на рис. 3.6, устройство состояло из экрана, прикрепленного одним концом к крышке стола. В начальном положении экран всей плоскостью лежал на столе. На глазах у ребенка экран медленно поворачивали в противоположную от него сторону, как разводной мост, до вертикального положения в 90 градусов, затем поворачивали дальше до полного полукруга в 180 градусов и снова клали плоскостью на стол. Затем экран поворачивали в противоположную сторону — по направлению к ребенку.

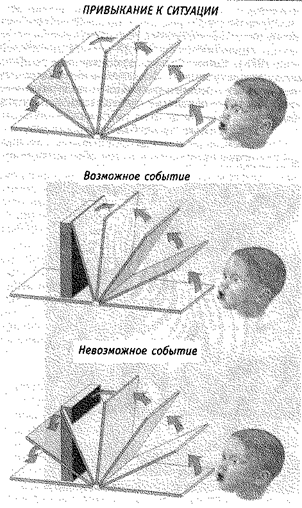
Рис. 3.6. Тестирование постоянства объекта.Детям показывают поворачивающийся экран, пока они не перестают на него смотреть. Коробка ставится туда, где экран может ее скрыть, и затем дети видят либо возможное событие (экран поворачивается, пока как бы не сталкивается с коробкой, а затем возвращается в исходное положение), либо невозможное событие (экран как бы проходит сквозь коробку). Дети уделяли больше внимания невозможному событию, показывая тем самым, что они знают о существовании скрытой за экраном коробки (адаптировано из: Baillargeon, 1987).

Когда этот вращающийся экран показывали младенцам в первый раз, они смотрели на него почти целую минуту, но после повторных попыток теряли интерес и обращали свое внимание куда-нибудь еще. В этот момент на столе, позади от места крепления экрана, появлялась ярко раскрашенная коробка; ее не было бы видно, если бы экран был поднят вертикально (на самом деле дети видели не настоящую коробку, а ее отражение). После этого, как показано на рис. 3.6, детям демонстрировали либо возможное событие, либо невозможное. Одна группа младенцев видела, как экран поворачивается из начального положения до того места, в котором он должен был бы столкнуться с коробкой; в этом месте экран останавливался и двигался назад, в исходное положение. Другая группа видела, как экран поворачивается до вертикального положения и затем продолжает поворачиваться дальше на другую сторону 180-градусной дуги, как будто никакой коробки у него на пути не было.

Экспериментаторы рассуждали так: если дети считают, что коробка все еще существует, даже когда ее скрывает экран, то их должно удивить, что экран проходит сквозь нее — невозможное событие, и тогда, следовательно, они будут смотреть на экран дольше, чем в том случае, когда экран как бы сталкивается с коробкой, прежде чем вернуться в первоначальное положение. Именно это и имело место. Несмотря на то, что невозможное событие было перцептивно идентичным событию, которое они уже много раз видели и потеряли к нему интерес, они находили его более интересным, чем событие физически возможное, но которого они никогда раньше не видели, — как экран останавливается на полпути к другому концу дуги и затем меняет направление (Baillargeon, Spelke & Wasserman, 1985).

Следует заметить, что детям в этом эксперименте было всего 4,5 месяца; они, таким образом, демонстрировали наличие у них знания о постоянстве объекта на 4-5 месяцев раньше, чем предсказывает теория Пиаже. При повторении этого исследования было обнаружено, что у некоторых младенцев в возрасте всего 3,5 месяца также имеется знание о постоянстве объекта (Baillargeon, 1987; Baillargeon & DeVos, 1991).

Задачи Пиаже на сохранение — это еще один пример того, как при более внимательном анализе сложных навыков, необходимых для успешного решения задачи, оказывается, что компетентность у детей наступает раньше, чем предсказывает его теория. Например, если условия эксперимента в тесте на сохранение подобраны тщательно, так чтобы ответы детей не зависели от их речевых способностей (т. е. от того, насколько хорошо они понимают, что имеет в виду экспериментатор под словами «больше» и «длиннее»), то даже у 3- и 4-летних детей обнаруживается знание о сохранении числа, т. е. они могут различать существенный признак (количество элементов в наборе) и несущественный (особенности пространственного расположения элементов) (Gelman & Gallistel, 1978).

В одном из исследований сохранения количества два набора игрушек были расположены в линию, одна к другой (как на рис. 3.5). Экспериментатор сказала ребенку, что один ряд — его, а другой — ее, и затем попросила ребенка высказаться о соотношении их количества. Например: «Вот твои солдатики, а это — мои солдатики. Каких больше: твоих или моих — или их поровну?» Получив исходное суждение ребенка, она расставила один ряд игрушек свободнее и повторила вопрос.

Сначала 5-летние дети не справлялись с задачей на сохранение количества и, как и предсказывал ранее Пиаже, говорили, что в длинном ряду «солдатиков больше». Но затем экспериментатор ввела другие условия. Она не стала говорить об этих игрушках как об отдельных солдатиках и вместо этого сказала: «Вот моя армия, а вот твоя армия. Чья армия больше: твоя или моя — или они одинаковые?» И после этой несложной перемены слов большинство детей оказались способны к сохранению количества и решили, что армии одинаковой величины, хотя одна из них и растянулась. Когда детям предложили интерпретировать то, что они видят, как нечто цельное, собранное воедино, а не как набор отдельных элементов, несущественные перцептивные преобразования стали меньше влиять на их суждения о равенстве (Markman, 1979).

В ходе других исследований были обнаружены другие различные факторы, способные оказать влияние на развитие конкретного операционного мышления. Например, некоторые культурные традиции могут оказывать влияние на овладение детьми решением задач, разработанных Пиаже (Rogoff, 1990). Кроме того, овладению решением этих задач может способствовать начало посещения школы (Artman & Canan, 1993). Эти и другие свидетельства позволяют предположить, что конкретное операционное рассуждение, возможно, является не универсальной стадией развития, характерной для среднего детского возраста, а продуктом культурной среды, школьного обучения, а также специфического формулирования вопросов и инструкций (Gellatly, 1987; Light & Perrett-Clermont, 1989; Robern, 1989).