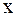Уравнения Лапласа и Пуассона
Уравнение
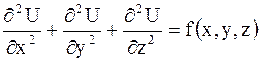
| (2.67) |
называется уравнением Пуассонав трехмерном пространстве. Если в этом уравнении 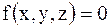 , то оно называется уравнением Лапласа:
, то оно называется уравнением Лапласа:
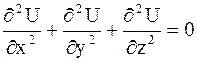 . .
| (2.68) |
К исследованию уравнений Лапласа и Пуассона приводит рассмотрение задач о стационарном процессе: это задачи гидродинамики, диффузии, распределения температуры, электростатики и др.
Эти уравнения относятся к уравнениям эллиптического типа.
Те задачи, которые приводят к уравнениям, содержащим время, называются нестационарными или динамическими задачами математической физики; задачи, приводящие к уравнениям, не содержащим время, называются стационарными или статическими.
Как было показано, уравнения математической физики имеют бесчисленное множество решений, зависящие от двух произвольных функций (речь идет об уравнениях второго порядка для функции двух переменных). Для того, чтобы из множества решений выделить определенное, характеризующее процесс, необходимо на искомую функцию наложить дополнительные условия, которые диктуются физическими соображениями. Таковыми условиями для уравнений в частных производных являются, чаще всего, начальные и граничные условия. Граничные условия – это условия заданные на границе рассматриваемой среды; начальные условия – это условия, относящиеся к какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Дополнительные условия, так же как и само дифференциальное уравнение, выводятся на основе физических соображений, связанных с самим процессом. Вместе с тем дополнительные условия должны быть такими, чтобы обеспечить выделение единственного решения из всего множества решений. Число граничных и начальных условий определяются типом уравнения, а их вид – заданным исходным состоянием на границе объекта и внешней среды. Для рассматриваемых нами уравнений число начальных условий равно порядку старшей производной по времени, входящей в уравнение, а число граничных условий – порядку старшей производной по координате.
Совокупность дифференциального уравнения и дополнительных условий представляют собой математическую формулировку физической задачи, и называется задачей математической физики.
Итак, задача математической физики состоит в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям, скажем, граничным и начальным.
Задача математической физики считается поставленной корректно, если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво.
2.19 КОЛЕБАНИЯ СТРУНЫ. ГРАНИЧНЫЕ И НАЧАЛЬНЫЕ УСЛОВИЯ. ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ
 Пусть струна находится под действием сильного начального натяжения
Пусть струна находится под действием сильного начального натяжения 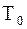 . Если вывести струну из положения равновесия и подвергнуть действию какой-либо силы, то струна начнет колебаться. Процесс колебания можно описать одной функцией
. Если вывести струну из положения равновесия и подвергнуть действию какой-либо силы, то струна начнет колебаться. Процесс колебания можно описать одной функцией 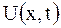 , характеризующей вертикальное перемещение струны (отклонение от положения равновесия (рис. 2.2)). При каждом фиксированном значении
, характеризующей вертикальное перемещение струны (отклонение от положения равновесия (рис. 2.2)). При каждом фиксированном значении 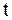 график функции
график функции 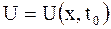 на плоскости
на плоскости 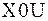 дает форму струны в момент времени
дает форму струны в момент времени 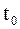 .
.
Функция 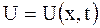 удовлетворяет уравнению
удовлетворяет уравнению
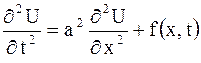 , ,
| (2.69) |
|
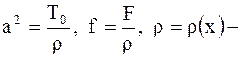 масса единицы длины (линейная плотность струны),
масса единицы длины (линейная плотность струны), 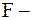 сила, действующая на струну перпендикулярно оси
сила, действующая на струну перпендикулярно оси 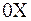 и рассчитанная на единицу длины.
и рассчитанная на единицу длины.
Если внешняя сила отсутствует, т.е. 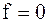 , то уравнение
, то уравнение
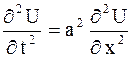
| (2.70) |
описывает свободные колебания струны без воздействия внешних усилий.
Уравнение (2.69) является простейшим уравнением гиперболического типа и в то же время одним из важнейших уравнений матфизики.
Одного уравнения движения (2.69) или (2.70) при математическом описании физического процесса недостаточно. При рассмотрении задачи о колебании струны дополнительные условия могут быть двух видов: начальные и граничные (краевые).
Так как процесс колебаний струны зависит от ее начальной формы и распределения скоростей, то следует задать начальные условия:
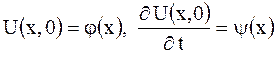 . .
| (2.71) |
Граничные условия определяются поддерживаемым на концах струны режимом на протяжении процесса колебания. Так, если концы струны длины 
закреплены, то отклонения  в точках
в точках 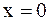 и
и 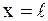 равны нулю:
равны нулю:
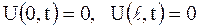 . .
| (2.72) |
Будем говорить о трех типах граничных условий:
I 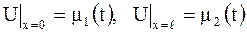
II 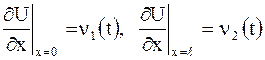
III 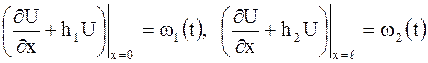 ,
,
где 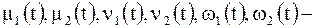 известные функции,
известные функции,
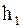 и
и 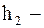 известные постоянные.
известные постоянные.
Приведенные условия называют соответственно граничными условиями первого, второго, третьего рода. Условия I имеют место в том случае, когда концы объекта (струна, стержень и т.д.) перемещаются по заданному закону; условия II – в случае, когда к концам приложены заданные силы; условия III – в случае упругого закрепления концов.
Если функции, заданные в правой части равенства, равны нулю, то граничные условия называются однородными. Так, граничные условия (2.72) – однородные. Комбинируя различные перечисленные типы граничных условий, получим шесть типов простейших краевых задач.
В том случае, когда режим на концах не будет оказывать существенного влияния на ту часть струны, которая достаточно удалена от них, струну считают бесконечной. В силу этого вместо полной краевой задачи ставят предельную задачу – з а д а ч у К о ш и: найти решение уравнения (2.69) для 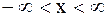 при
при 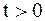 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
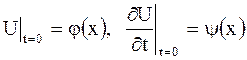 .
.
Если изучается процесс вблизи одной границы и влияние граничного режима на второй границе не имеет существенного значения на протяжении интересующего нас промежутка времени, то приходим к постановке задачи на полуограниченной прямой 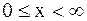 . В этом случае задаются начальные условия и одно из граничных условий I - III при
. В этом случае задаются начальные условия и одно из граничных условий I - III при 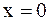 .
.
Дата добавления: 2018-11-26; просмотров: 535;