Элементы теории самоорганизованной критичности

Системы, состоящие из многих взаимодействующих элементов, постоянно самоорганизуются и могут достичь некоторого критического состояния, в котором даже малое событие вызывает цепную реакцию, могущую привести к катастрофе. Когда происходит что-то непредвиденное или катастрофа, то всегда ищут причину. Например, когда узнали о гибели динозавров по отпечаткам на окаменелостях, одни палеонтологи приписали их исчезновение падению крупного метеорита, другие — извержению вулкана. Землетрясение геологи связывают с неустойчивостью вдоль разлома земной коры. Когда рушится рынок акций, находят где-то неконтролируемую продажу товара.

При исследовании сложных систем часто пользуются теми же методами, что и при исследовании простых систем, так как они хорошо разработаны и проверены. Большую систему делят на малые подсистемы, изучают каждую из них по отдельности и считают, что реакция или отклик в каждой из них пропорционален внешнему возмущению. Описывают динамику больших систем в терминах равновесного состояния, которое изредка нарушается внешним воздействием. Но оказалось, что многие хаотические системы не поддаются такому анализу. П. Баком, К.Визенфельдом и Ч.Тангом (США) была разработана теория самоорганизованной критичности.

Согласно этой теории, многие составные части системы эволюционируют естественным образом к критическому состоянию, в котором малое возмущение может вызвать цепную реакцию, способную повлиять на любое число элементов системы. И хотя в составных частях происходит больше незначительных событий, чем катастроф, цепные реакции разных масштабов вошли в динамику системы, т. е. малые события вызывает тот же механизм, что и крупные. Кроме того, составные части системы не достигают равновесия, а эволюционируют от одного метастабильного состояния к другому. Считается, что глобальные характеристики не зависят от микроскопических механизмов, поэтому их нельзя понять, разбивая систему на подсистемы и анализируя их отдельно. Эта модель исследовалась и улучшила понимание процессов в эволюции земной коры, на рынке акций, в экосистемах и других больших системах, которые ранее анализировали по частям.

Идея теории самоорганизованной критичности началась с наблюдений и опытов с кучей песка. Г.Хелд, проводивший эксперименты по компьютерному моделированию, разработал устройство, которое медленно и равномерно — по одной песчинке — насыпало песок на круглую подложку. Песчинки сначала оставались в месте падения, потом громоздились в кучу, а когда склон становился очень крутым и достигалось критическое состояние, одна песчинка вызывала катастрофу. Песчинка падала сначала спокойно, но, достигнув неустойчивых песчинок, вызывала лавину — разновидность цепной реакции или ветвящегося процесса. Как только «активные» песчинки скатывались с кучи, процесс прекращался. Куча сохраняла свою крутизну и высоту, потому что вероятности прекращения активности и ее ветвления в среднем равны. Если крутизна будет меньше критической, то лавины будут слабее, а при большей кривизне — значительно возрастут.

Эксперименты с мокрым песком показали, что сначала лавины будут меньшего размера, чем в сухой куче, и крутизна превзойдет критическую, но затем резко произойдут обвалы и падения. Такая система неустойчива по многим параметрам, а ее критическое состояние весьма

устойчиво («суб- и суперкритические» крутизны стремятся стать «критическими», сбрасывая лишние песчинки). Хотя песок сыплется с постоянной скоростью, его количество меняется со временем, и график этой величины — хаотический сигнал разных длительностей. Возникающие при этом структуры, полученные при различных типах деформации мокрого песка в Институте горного дела СО РАН (Новосибирск, 1984), упорядочены (рис. 13.9).

Сигнал называют фликкер-шумом или шумом мерцания типа

1/f, если прошлые события в памяти сохраняются. «Белый», или «случайный», шум означает отсутствие корректировки динамики с прошлыми событиями. Шум мерцания широко распространен в природе: в активности Солнца и излучении галактик, в протекающем через резистор токе, в потоке воды в реке. Шум мерцания содержит наборы всех длительностей и всех амплитуд сигналов, возникающих, когда система, находящаяся в критическом состоянии, порождает цепные реакции всех амплитуд и длительностей.

Построенная в то же время математическая модель помогла понять динамику землетрясений, экосистем и турбулентности в жидкости. Еще в 1956 г. геологи Бено Гутенберг и Чарлз Рихтер (введший шкалу Рихтера) установили закон связи числа сильных и слабых землетрясений, который носит их имена. Согласно этому закону, число землетрясений, высвобождающих за год определенное количество энергии Е, пропорционально Е^-b, где b 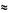1,5, и не зависит от географического района. Следовательно, сильные землетрясения происходят реже слабых, и все они связаны с одним и тем же процессом. В качестве последнего обычно называют механизм проскальзывания: блоки коры слипаются, а затем скользят относительно других блоков, образуя разломы. При скольжении блоков возникшее напряжение снимается и распространяется на соседние районы.

Этот механизм был проверен на опытах, поставленных В.Бобровым и М.Лебедкиным, наблюдавшими «землетрясения», амплитуда и частота которых были связаны степенным законом. Они провели опыты с алюминиевым и ниобиевым стержнями и получили близкие результаты, хотя механизмы процессов в земной коре и модели отличались. Потом была создана компьютерная модель земной коры, состоящая из двух плит, — упругой и жесткой, взаимодействующих посредством трения. На этой модели результаты проверялись несколько раз, при этом записывались распределения сил до и после взаимодействия, а не детали динамики. Сначала регистрировались слабые «землетрясения», потом система эволюционировала к критическому состоянию, в котором регистрируются как слабые, так и сильные «землетрясения». Равномерное увеличение силы в целом уравновешивалось высвобождением ее на границе. Энергия, выделяемая во время землетрясения, связана в модели с числом событий проскальзывания, происходящих после возникновения одиночной неустойчивости в каком-то «эпицентре». Если подсчитать число землетрясений каждой величины за длительный период, то получается закон Гутенберга—Рихтера (рис. 13.10). Катастрофические землетрясения представлены частью графика, относящейся к более высоким значениям энергии, а слабые — к низким. С.Обухов показал, что в четырех и более измерениях отдельные ветвящиеся процессы не

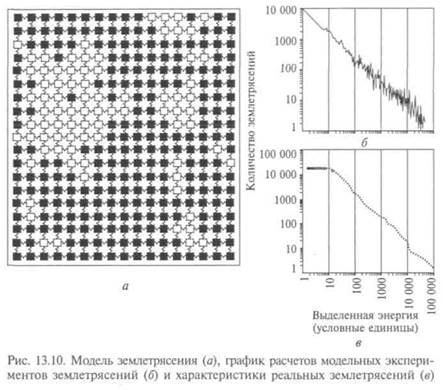зависимы и b = 1,5. Это подтверждает предположение о том, что земная кора находится в критическом состоянии.

Эта модель не только объясняет эволюцию землетрясений, но и описывает распределение их эпицентров. Степенные законы и ранее применяли для анализа распределений таких объектов, как горы, облака, галактики, вихри в турбулентных потоках. Показатель степени числа r вычисляется по числу объектов внутри сферы радиуса r. Такое распределение называют фракталом, и число фракталов в природе велико. Авторы описываемой теории считают фракталы мгновенными «срезами» самоорганизующихся критических процессов. Фрактальные структуры и шум мерцания — пространственные и временные «отпечатки» самоорганизованной критичности.

Задача прогнозирования землетрясений осложнена зависимостью от начальных условий; кроме того, иногда сказывается влияние событий, далеких от эпицентра. Численные эксперименты показали, что неопределенность начальных условий растет со временем по степенному, а не по экспоненциальному закону, как в системах с развитым хаосом, т.е. соответствует эволюции на грани хаоса или состоянию «слабого хаоса». В этом проявляется самоорганизованная критичность, и поэтому некоторые прогнозы возможны. Например, если погода есть явление хаотическое и 100 обсерваторий собирают достаточно информации на двухдневный прогноз, то 1000 обсерваторий могли бы обеспечить прогноз на четыре дня. Если погода — явление слабохаотическое, то 1000 обсерваторий обеспечили бы прогноз на 20 дней вперед. Вместо погоды можно говорить о куче песка или землетрясениях. Например, если известно, что распределение автомобилей на дорогах описывается шумом мерцания, то движения с попеременными остановками и троганием с места можно рассматривать как критические лавины, которые распространяются по потоку автомобилей.

В рассмотренных выше случаях теория самоорганизованной критичности применялась к системам с сохраняющимся числом частиц. Анализируя игру Конуэя «Жизнь», имитирующую возрастание сложности в биосистеме, авторы данной теории установили, что распределение живых ячеек является фракталом, который можно описать степенным законом с показателем степени 1,7. Таким образом, число живых ячеек колебалось со временем так же, как размеры лавин в куче песка, и система самоорганизовалась в критическое состояние.

Флуктуации в экономике, как заключили Ф.Андерсон и Б.Артур, также могут быть вызваны лавинами в самоорганизованном критическом состоянии системы. Б. Мандельброд из корпорации IBM проанализировал такие показатели, как индекс Доу-Джонса, и обнаружил флуктуации, соответствующие шуму мерцания. Различные метастабильные состояния экономики могут быть рассмотрены как метастабильные состояния кучи песка или земной коры. В других экономических моделях состояния более устойчивы, и большие агрегатные флуктуации могут возникать только от внешних ударов, влияющих на разные секции одинаково. Но причины их отыскать трудно, пример тому — депрессия 30-х гг. XX в. в США. В модели самоорганизованной критичности причины могут быть и при отсутствии таких «толчков». Большие флуктуации являются внутренним и неизбежным свойством динамики этой модели экономики. Такая проверка была проделана, и оказалось, что при изменении спроса на продукт нескольких компаний случайным образом на малую величину может возникнуть «лавина» в продаже и производстве.

Вопросы для самопроверки и повторения

1. В чем заключается явление самоорганизации? Приведите примеры из области химии и физики. Почему они не могут быть описаны с позиций классической науки?

2. Как строится термодинамика открытых систем? Что такое устойчивые и неустойчивые равновесные состояния? Поясните понятия простой и сложной системы.

3. Как возникают структуры из хаоса в неорганической и живой материях? Каковы условия их образования? Приведите примеры из разных областей естествознания.

4. Что такое синергетика и каково ее значение для современной картины мира? Каков механизм эволюции в соответствии с представлениями синергетики?

5. Какие этапы можно выделить в развитии самоорганизующихся систем? Что такое фазовое пространство и как оно используется в моделировании сложных систем?

6. Поясните понятие диссипативной структуры по И.Пригожину.

7. Каково соотношение случайного и закономерного в концепции развития? Какую роль сыграл принцип элементарного беспорядка в естествознании?

8. Поясните понятия «хаос», «бифуркация», «катастрофа». Как теория катастроф связана с синергетикой?

9. Какие системы могут находиться в высокоупорядоченном состоянии? Каковы необходимые условия возникновения «самоорганизации» и существуют ли достаточные?

10. Дайте представление о прямой и обратной связях в сложной систе
ме. Поясните связь процессов в земной коре с теорией самоорганизован
ной критичности. Дайте примеры использования этой теории.