вычислительных задач
18.1. Классы сложности P и NP и их взаимосвязь
Установление прямых нижних оценок сложности вычислений, о которых шла речь в предыдущем разделе, удается лишь в очень редких случаях. В связи с этим получил распространение подход, связанный с получением косвенных нижних оценок, т.е. установление таких утверждений, в которых существование эффективного разрешающего алгоритма для конкретной задачи влечет за собой существование эффективного алгоритма для многих общепризнанно трудных задач.
Нам необходимо формализовать соответствующий подход. Пусть П — некоторая массовая задача, характеризуемая множеством параметров, I Î П — индивидуальная задача, в которой эти параметры фиксированы. Пусть с массовой задачей П связана и зафиксирована схема кодирования a, которая ставит каждой индивидуальной задаче I Î П в соответствие слово a(I) в некотором алфавите А. При этом под размером задачи I понимается длина слова a(I). Пусть Т — машина Тьюринга, решающая задачу П и 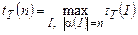 — соответствующая функция временной сложности (по худшему случаю).
— соответствующая функция временной сложности (по худшему случаю).
Говорят, что машина Т решает задачу П за полиномиальное время, если 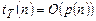 для некоторого полинома р.
для некоторого полинома р.
В противном случае говорят, что машина Т решает задачу П за экспоненциальное время. Заметим, что при данном определении к экспоненциальным оценкам относятся, например, оценки вида 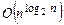 . (Некоторые авторы оценки такого вида называют субэкспоненциальными, под которыми понимаются такие оценки, которые превосходят любой полином, но меньше, чем
. (Некоторые авторы оценки такого вида называют субэкспоненциальными, под которыми понимаются такие оценки, которые превосходят любой полином, но меньше, чем 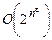 для любого e > 0.
для любого e > 0.
Про задачу П говорят, что она разрешима за полиномиальное время, если существует машина Тьюринга Т, решающая ее за полиномиальное время. Обозначим через Р класс задач, разрешимых за полиномиальное время. Относительно класса Р необходимо сделать следующие замечания.
1. В определении Р существенным является фиксация схемы кодирования a. Многие естественные схемы кодирования полиномиально эквивалентны, т.е. позволяют переходить от одного кода задачи к другому коду за полиномиальное время от длины кода. В этом случае принадлежность (или не принадлежность) задачи П классу Р определяется инвариантно по отношению к схемам кодирования. Однако это справедливо не всегда и, вообще говоря, класс сложности Р зависит от схемы кодирования, поэтому там, где схема кодирования не очевидна или может повлиять на класс сложности, ее следует указывать явно.
2. Класс Р определен через функцию временной сложности машины Тьюринга. Можно сделать соответствующие определения через любую другую алгоритмическую модель.
Однако имеется ряд фактов о полиномиальной эквивалентности временных функций сложности многих типов вычислительных моделей, что позволяет утверждать, что класс Р определен однозначно для «разумных» вычислительных моделей[9].
Поэтому без специальных оговорок будут допускаться выражения типа «алгоритм А имеет полиномиальную сложность» или «алгоритм В имеет экспоненциальную сложность». Обратим внимание, что имеется существенное различие между алгоритмами полиномиальной и экспоненциальной сложности. Ясно, что любой полиномиальный алгоритм более эффективен при достаточно больших размерах входа. Кроме того, полиномиальные алгоритмы лучше реагируют на рост производительности ЭВМ. Рассмотрим такой параметр, как размер решаемой задачи на ЭВМ за единицу времени с помощью данного алгоритма. Тогда изменение данного параметра при переходе к ЭВМ в 100 раз и в 1000 раз большей производительности для различных функций временной сложности показан в табл.18.1.
Таблица 18.1
| Функция временной сложности | Размер решаемой задачи на современной ЭВМ за сутки | То же на ЭВМ в 100 раз быстрых | То же на ЭВМ в 1000 раз быстрых |
| n | N1 | 100 N1 | 1000 N1 |
| n2 | N2 | 10 N2 | 31.6 N2 |
| n3 | N3 | 4.64 N3 | 10 N3 |
| 2n | N4 | 6.64 + N4 | 9.97 + N4 |
| 3n | N5 | 4.19 + N5 | 6.29 + N5 |
Из табл.18.1 видно, что в случае полиномиальных алгоритмов размер решаемой задачи при увеличении производительности ЭВМ увеличивается на мультипликативную константу, тогда как для экспоненциальных алгоритмов имеет место увеличение на аддитивную константу.
Далее, полиномиальные алгоритмы обладают свойством «замкнутости», — можно комбинировать полиномиальные алгоритмы, используя один в качестве «подпрограммы» другого и при этом результирующий алгоритм будет полиномиальным. В силу приведенных причин используется следующая терминология: полиномиальные алгоритмы называют эффективными, полиномиально решаемые задачи называют легкорешаемыми, а экспоненциально решаемые задачи называют труднорешаемыми.
Для практики важным является классификация задач по признаку труднорешаемости, хотя следует заметить, что установление легкорешаемости задачи еще не означает ее практическую решаемость. Например, установление полиномиальной оценки 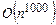 не гарантирует практической решаемости уже при начальных значениях n. Аналогичное замечание можно сделать относительно труднорешаемости. Заметим, что труднорешаемость задачи может быть связана с тем, что ее решение настолько велико, что не может быть записано в виде выражения, длина которого была бы ограничена полиномом от длины входа. Чтобы исключить этот тип труднорешаемости, рассматривается только такие задачи, которые имеют «короткий» ответ.
не гарантирует практической решаемости уже при начальных значениях n. Аналогичное замечание можно сделать относительно труднорешаемости. Заметим, что труднорешаемость задачи может быть связана с тем, что ее решение настолько велико, что не может быть записано в виде выражения, длина которого была бы ограничена полиномом от длины входа. Чтобы исключить этот тип труднорешаемости, рассматривается только такие задачи, которые имеют «короткий» ответ.
Рассмотрим несколько примеров.
1. Пусть М = {1, 2, …, n} — конечное множество и R Í MxM — бинарное отношение на М. Рассмотрим задачу проверки — является ли R отношением эквивалентности. Будем задавать индивидуальную задачу матрицей AR = (aij), i, j Î 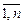 , где
, где
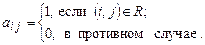
Ясно, что R будет отношением эквивалентности тогда и только тогда, когда матрица AR имеет единичную диагональ, симметрична и выполнено соотношение 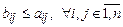 , где
, где 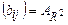 — матрица отношения R2.
— матрица отношения R2.
Кроме того, выполнено 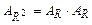 , где имеется в виду булево умножение матриц. Ясно, что сложность рассматриваемой задачи
, где имеется в виду булево умножение матриц. Ясно, что сложность рассматриваемой задачи 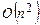 .
.
Бинарное отношение R называется связным, если для любых i, j Î 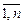 существует k такое, что выполнено
существует k такое, что выполнено 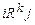 .
.
2. Бинарное отношение R называется эйлеровым, если элементы R можно так упорядочить 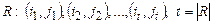 , что выполнено
, что выполнено 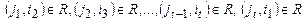 . Ясно, что эйлерово отношение является связным.
. Ясно, что эйлерово отношение является связным.
Можно доказать, что связное отношение R является эйлеровым тогда и только тогда, когда число единиц в матрице AR совпадает в i-м столбце и в i-й строке для каждого i Î 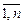 . Это дает алгоритм сложности
. Это дает алгоритм сложности 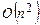 , проверяющий эйлеровость отношения R. Ясно, что связность отношения R проверяется за
, проверяющий эйлеровость отношения R. Ясно, что связность отношения R проверяется за 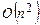 действий.
действий.
Заметим, что здесь главным для нас является установление полиномиальности рассматриваемых задач, а не установление наилучших алгоритмов.
3. Бинарное отношение R называется гамильтоновым, если элементы М можно так упорядочить i1, i2, …, in, что выполнено соотношение
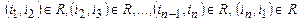 .
.
В настоящее время неизвестно полиномиального алгоритма от n проверки гамильтоновости произвольного отношения R. Тривиальный алгоритм требует n! упорядочений множества М и проверки условий (7), что, конечно, превосходит по величине любой полином от n.
4. Пусть f(x1, …, xn) — формула от булевых переменных x1, …, xn в некотором фиксированном базисе В. Напомним, что формула f(x1, …, xn) называется выполнимой, если существует набор значений переменных 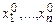 , такой, что
, такой, что 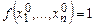 . Формула f(x1, …, xn) называется мультиафинной, если она имеет вид f(x1, …, xn) =
. Формула f(x1, …, xn) называется мультиафинной, если она имеет вид f(x1, …, xn) = 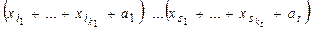 , где a1, …, at — константы, т.е. f представляет собой конъюнкцию линейных форм.
, где a1, …, at — константы, т.е. f представляет собой конъюнкцию линейных форм.
Рассмотрим задачу проверки выполнимости мультиафинной формулы. Ясно, что существование выполняющего набора для мультиафинной формулы сводится к существованию решения линейной системы уравнений над полем F2. Алгоритм Гаусса дает оценку 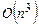 , поэтому рассматриваемая задача полиномиальна.
, поэтому рассматриваемая задача полиномиальна.
Пусть формула f(x1, …, xn) имеет конъюнктивную нормальную форму, т.е. имеет вид:
f(x1, …, xn) = 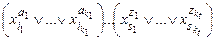 ,
,
где ai, …, zi — константы. Рассмотрим задачу проверки выполнимости для формул КНФ. В настоящее время неизвестно алгоритма полиномиальной сложности решения данной задачи. Тривиальный алгоритм требует перебор 2n наборов значений 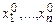 переменных и вычисления для каждого из них значения формулы.
переменных и вычисления для каждого из них значения формулы.
5. Рассмотрим стандартную задачу линейного программирования: для данных целочисленной (mxn)-матрицы А, m-вектора b и n-вектора c:
а) найти n-вектор x с рациональными координатами такой, что x ³ 0 и Ax = b, cT×x à min; либо
b) установить, что не существует n-вектора x такого, что x ³ 0 и Ax = b; либо
с) установить, что множество {cT×x: x ³ 0 и Ax = b} не ограничено снизу.
Хачиян Л.Г. (1979) установил, что данная задача принадлежит классу Р и тем самым разрешил вопрос, долго стоявший открытым.
Определим теперь класс NP задач распознавания, т.е. имеющих ответ «ДА» или «НЕТ». Для того, чтобы задача I содержалась в классе NP требуется только, чтобы в случае, если I имеет ответ «ДА», существовало бы слово с(I) длины, ограниченной полиномом от размера I такое, что задача с начальными данными с(I), I принадлежит Р. Слово с(I) называется удостоверением или догадкой для задачи I.
Рассмотрим примеры.
1. Пусть дана задача проверки гамильтоновости бинарного отношения R Í MxM на множестве М = {1, 2, …, n}. Если R — гамильтоново отношение, то удостоверением этого будет последовательность элементов М: с(R) = i1i2…in. Имея пару с(R), R, легко убеждаемся, проверяя соотношения (7), верно ли, что R — гамильтоново отношение. Следовательно, задача проверки гамильтоновости бинарного отношения лежит в классе NP.
2. Пусть дана задача проверки выполнимости формул КНФ. Если f(x1, …, xn) — выполнимая функция, то удостоверением этого будет соответствующий выполняющий набор 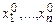 . Имея пару (
. Имея пару ( 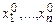 ), f(x1, …, xn), легко убедиться, верно ли, что f(x1, …, xn) выполнима.
), f(x1, …, xn), легко убедиться, верно ли, что f(x1, …, xn) выполнима.
Формализуем теперь данные идеи. Класс NP определяется через понятие недетерминированного алгоритма. Введем понятие недетерминированной машины Тьюринга.
Схема недетерминированной машины Тьюринга приведена на рис.18.1.
| … | * | x1 | x2 | … | xn | ||||||||||||
| -3 | -2 | -1 | … | n | |||||||||||||

Рис.18.1
Отличие от обычной машины Тьюринга заключается в том, что недетерминированная машина (НТ) имеет дополнительно угадывающий модуль (УМ), который может только записывать на ленту слова из внешнего алфавита. Поскольку речь идет о задачах распознавания, то удобно считать, что машина имеет два заключительных состояния qY и qN, соответствующие ответам «ДА» и «НЕТ» соответственно. Работа машины имеет две стадии:
1-я стадия — угадывание. В начальный момент на ленте записано слово x = x1…xn — код индивидуальной задачи I, начиная с ячейки 1. В ячейке 0 записан знак раздела *. Угадывающий модуль просматривает ячейку –1. Затем УМ пишет произвольное слово с(х) по одной букве за такт в каждой ячейке с номерами — –1, –2, –3, … . В итоге 1-й стадии конфигурацией машины будет с(х)*q1x.
2-я стадия — решение. На этой стадии недетерминированная машина работает как обычная машина Тьюринга с конфигурации с(х)*q1x. Если машина через конечное число шагов приходит в состояние qY, то говорим, что она принимает конфигурацию с(х)*q1x. Будем говорить, что недетерминированная машина принимает x, если существует слово с(х), такое что конфигурация с(х)*q1x принимается.
Определим время работы недетерминированной машины, положив 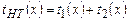 , (если х принимается), где
, (если х принимается), где 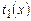 — время работы на стадии 1, т.е., по определению,
— время работы на стадии 1, т.е., по определению, 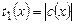 ;
; 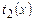 — время работы на стадии 2, т.е., по определению,
— время работы на стадии 2, т.е., по определению, 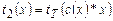 (Т — соответствующая (обычная) машина Тьюринга).
(Т — соответствующая (обычная) машина Тьюринга).
Определим 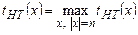 . Недетерминированная машина НТ решает задачу П за полиномиальное время, если
. Недетерминированная машина НТ решает задачу П за полиномиальное время, если 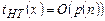 для некоторого полинома р.
для некоторого полинома р.
Заметим, что временная функция определена только для тех индивидуальных задач х, которые принимаются машиной НТ.
Определим класс задач NP как множество задач, для которых существует недетерминированная машина Тьюринга, принимающая за полиномиальное время те и только те слова, которые соответствуют индивидуальным задачам с ответом «ДА».
Разберем теперь вопрос о взаимоотношении между введенными классами Р и NP. Ясно, что Р Í NP. Имеется много причин считать это включение строгим, однако этот факт пока не доказан (1992).
Теорема 18.1. Если задача П Î NP, то существует такой полином р, что П может быть решена детерминированным алгоритмом со сложностью 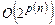 , n — размер П.
, n — размер П.
Доказательство. Пусть НТ — недетерминированная машина Тьюринга, решающая задачу П, и q(n) — полином, ограничивающий временную функцию сложности НТ. Не нарушая общности, можно считать, что q(n)= 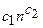 (с1, с2 – константы). По определению класса NP, если вход х длины n принимается НТ, то существует слово с(х) длины не более чем q(n), такое, что НТ дает ответ «ДА» не более чем за q(n) шагов. Значит, общее число возможных слов-догадок не более чем kq(n), где k — мощность внешнего алфавита НТ. Считаем, что все догадки имеют длину q(n), в противном случае их можно подравнять. Теперь можно представить детерминированный алгоритм решения задачи П, который на каждом из kq(n) слов-догадок реализует 2-ю стадию работы НТ и работает q(n) тактов. Алгоритм дает ответ «ДА», если найдется слово-догадка, приводящее к принимающему вычислению. Время работы данного алгоритма q(n)kq(n). Ясно, что существует подходящий полином р(n) такой, что сложность описанного алгоритма не превосходит
(с1, с2 – константы). По определению класса NP, если вход х длины n принимается НТ, то существует слово с(х) длины не более чем q(n), такое, что НТ дает ответ «ДА» не более чем за q(n) шагов. Значит, общее число возможных слов-догадок не более чем kq(n), где k — мощность внешнего алфавита НТ. Считаем, что все догадки имеют длину q(n), в противном случае их можно подравнять. Теперь можно представить детерминированный алгоритм решения задачи П, который на каждом из kq(n) слов-догадок реализует 2-ю стадию работы НТ и работает q(n) тактов. Алгоритм дает ответ «ДА», если найдется слово-догадка, приводящее к принимающему вычислению. Время работы данного алгоритма q(n)kq(n). Ясно, что существует подходящий полином р(n) такой, что сложность описанного алгоритма не превосходит 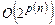 , что и требовалось доказать.
, что и требовалось доказать.
Относительно класса NP следует сделать несколько замечаний:
класс NP один и тот же для различных вычислительных моделей, использующих недетерминированные операции;
класс P замкнут относительно дополнения задач. Для класса NP этого утверждать нельзя.
Дополнением 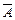 задачи распознавания А называют задачу, в которой коды задач с ответом «ДА» в точности соответствует кодам задач А, которые не имеют ответа «ДА». Класс задач, являющихся дополнениями к задачам класса NP обозначают СО-NP.
задачи распознавания А называют задачу, в которой коды задач с ответом «ДА» в точности соответствует кодам задач А, которые не имеют ответа «ДА». Класс задач, являющихся дополнениями к задачам класса NP обозначают СО-NP.
18.2. NP-полные задачи. Теорема Кука
Если P ¹ NP, то задачи из NP\P являются труднорешаемыми. Цель дальнейших результатов состоит в доказательстве того, что существуют конкретные задачи П, для которых справедливо включение П Î NP\P, если P ¹ NP. Соответствующие результаты основаны на понятии полиномиальной сводимости задач. Пусть П1, П2 — две задачи распознавания, задаваемые в алфавитах А1 и А2 соответственно. Будем говорить, что задача П1 полиномиально сводится к задаче П2 (обозначение: П1 µ П2), если существует словарная функция 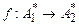 такая, что выполнены условия:
такая, что выполнены условия:
f — полиномиально вычислима;
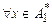 выполнено: х — индивидуальная задача П1 с ответом «ДА» Û
выполнено: х — индивидуальная задача П1 с ответом «ДА» Û 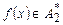 — индивидуальная задача П2 с ответом «ДА».
— индивидуальная задача П2 с ответом «ДА».
Утверждение 18.2. Если выполнено П1 µ П2 и П2 Î P, то П1 Î P.
Доказательство. Предложим полиномиальный алгоритм решения задачи П1: 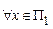 находим f(x) Î П2 и применяем к f(x) полиномиальный алгоритм, существующий по условию. Если получен ответ «ДА», то х имеет ответ «ДА». В противном случае х имеет ответ «НЕТ». Время работы алгоритма не превосходит
находим f(x) Î П2 и применяем к f(x) полиномиальный алгоритм, существующий по условию. Если получен ответ «ДА», то х имеет ответ «ДА». В противном случае х имеет ответ «НЕТ». Время работы алгоритма не превосходит 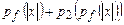 , где pf — полином, ограничивающий время вычисления функции f, участвующей в сведении П1 µ П2, p2 — полином, ограничивающий время решения задачи П2. Доказательство завершено.
, где pf — полином, ограничивающий время вычисления функции f, участвующей в сведении П1 µ П2, p2 — полином, ограничивающий время решения задачи П2. Доказательство завершено.
Утверждение 18.3. Если выполнено П1 µ П2 и П2 µ П3, то П1 µ П3.
Доказательство очевидно, так как функция f3(x) = f2(f1(x)) осуществляет сведение П1 µ П3, если f1, f2 дают сведения П1 µ П2, П2 µ П3 соответственно.
Определение 18.4. Задача П называется NP-полной, если выполнено:
а) П Î NP;
б) П1 µ П для любой задачи П1 Î NP.
Задача П называется NP-трудной, если для нее выполнено условие б).
Обозначим через NPС класс NP-полных задач, а через NPН — класс NP-трудных задач.
Согласно определению имеем:
NPС Ç P ¹ Æ Þ P = NP,
NPH Ç P ¹ Æ Þ P = NP,
NPС Ç (NP\P) ¹ Æ Þ NPС Ç P = Æ.
Другими словами, если для какой-то NP-полной задачи существует полиномиальный разрешающий алгоритм, то и для любой задачи из класса NP существует полиномиально разрешающий алгоритм. То же высказывание справедливо относительно NP-трудной задачи. Если какая-то NP-полная задача не лежит в классе Р, то и все NP-полные задачи не лежат в классе Р.
Утверждение 18.4. Если задачи П1, П2 Î NP, П1 µ П2 и П1 Î NPС, то П2 Î NPС.
Доказательство. Пусть П’ Î NP — произвольная задача. Тогда по определению П’ µ П1. Поскольку по условию П1 µ П2, то согласно утверждения 18.3 имеем П’ µ П2, что и доказывает данное утверждение.
Отсюда получаем способ доказательства NP-полноты конкретных задач, используя полиномиальное сведение к ней другой NP-полной задачи. Этот же способ пригоден и для доказательства NP-трудности задачи. Напомним, что классы NPC и NPH определяются только выполнимостью условий а), б) для NPC и условия б) для NPH.
Докажем теперь важную теорему Кука С. (1971), дающую первый пример NP-полной задачи.
Теорема 18.5. Задача проверки выполнимости произвольной КНФ является NP-полной задачей.
Доказательство. Пусть ВЫП — идентификатор данной задачи. В предыдущем разделе было показано, что ВЫП Î NP. Пусть П — произвольная задача из NP. Необходимо показать, что П µ ВЫП. Для этого множество индивидуальных задач LП с ответом «ДА» представим в стандартном виде соответствующей недетерминированной машиной Тьюринга (обозначение: НДМТ), работающей полиномиальное время и принимающей множество LП. Такое представление дает общую сводимость задачи, решаемой НДМТ за полиномиальное время.
Пусть распознающая множество LП НДМТ имеет алфавиты А, Q и функцию переходов (программу) 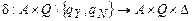
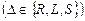 , р(n) — верхняя граница времени вычисления. Функцию fL, осуществляющую полиномиальное сведение П µ ВЫП, опишем в терминах работы НДМТ.
, р(n) — верхняя граница времени вычисления. Функцию fL, осуществляющую полиномиальное сведение П µ ВЫП, опишем в терминах работы НДМТ.
В вычислениях участвуют ячейки ленты с номерами от -р(n) до р(n) + 1, и при этом требуется учесть не более р(n) + 1 тактов работы НДМТ. Проверяющее вычисление определяется заданием в каждый момент времени содержания ячеек с указанными номерами, внутреннего состояния машины и положения считывающей головки. Соответствующие вычисления опишем в виде КНФ, использующей полиномиальное число дизъюнкций. Фиксируем нумерацию в алфавитах:
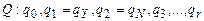
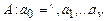 .
.
Условимся, что фраза «в момент времени i» означает «после выполнения i-го шага работы». Если вычисление закончилось раньше времени p(n), то конфигурация не меняется во все моменты после остановки. В нулевой момент на ленте записано слово х в ячейках с номерами 1, …, n. Слово-догадка w пишется в ячейках с номерами –1, …, –|n|. Остальные ячейки пусты. Описывая принимающее вычисление, необходимо учесть, что:
а) в ячейках пишется точно один символ;
b) машина находится точно в одном состоянии;
с) головка может просматривать точно одну ячейку с номером от –p(n) до p(n) + 1;
d) машина работает по программе.
Определим сначала переменные и их смысл с помощью табл.18.2.
Таблица 18.2
| Переменная | Пределы изменения индексов | Смысл |
| Q(i, k) | 0 £ i £ p(n) 0 £ k £ r | В момент времени i машина находится в состоянии qk |
| H(i, j) | 0 £ i £ p(n) –p(n) £ j £ p(n) + 1 | В момент времени i головка просматривает ячейку с номером j |
| A(i, j, k) | 0 £ i £ p(n) –p(n) £ j £ p(n) + 1 0 £ k £ r | В момент времени i в j-ю ячейку записан символ ak |
Описание сводящей функции fL для П µ ВЫП дадим в виде набора дизъюнкций, конъюнкцией которых и будет fL. При этом выполняющий набор значений истинности однозначно соответствует принимающему вычислению на х, стадия проверки занимает время не большее p(n) шагов, слово-догадка имеет длину не более p(n), причем:
x Î LП Û на х существует принимающее вычисление;
Û на х существует принимающее вычисление с временем £ p(n) и |w| £ p(n);
Û существует выполняющее значение переменных для задачи fL(x), заданной КНФ.
При этом fL(x) вычисляется за полиномиальное время.
Определим множества дизъюнкций и их смысл.
G1 в любой момент времени i машина находится точно в одном состоянии;
G2 в любой момент времени i головка просматривает точно одну ячейку;
G3 в любой момент времени i каждая ячейка содержит точно один символ А;
G4 в момент времени 0 вычисление находится в начальной конфигурации стадии проверки со входом х;
G5 не более чем через p(n) шагов машина переходит в состояние qY (принимает х);
G6 для любого момента времени i, 0 £ i £ p(n) конфигурация машины в момент i + 1 получается из конфигурации в момент i однократным применением команды машины.
Описание дизъюнкций для функции fL.
| G1 | (Q(i, 0) Ú Q(i, 1) Ú … Ú Q(i, r)) | 0 £ i £ p(n) |
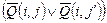
| 0 £ i £ p(n) 0 £ i < j’ £ r | |
| G2 | (H(i, ‑p(n)) Ú H(i, ‑p(n) + 1) Ú … Ú Ú H(i, p(n) + 1)) | 0 £ i £ p(n) |
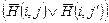
| 0 £ i £ p(n) –p(n) £ i < j’ £ £ p(n) + 1 | |
| G3 | (a(i, j, 0) Ú a(i, j, 1) Ú … Ú a(i, j, v) | 0 £ i £ p(n) |
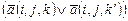
| ‑p(n) £ j £ p(n) + 1 0 £ k < k’ £ v | |
| G4 | (Q(0, 0)), (H(0, 1)), (a(0, 0, 0)),
(a(0, ‑1, 0)), …, (a(0, ‑p(n), 0)),
(a(0, 1, k1)), …, (a(0, n, kn)),
(a(0, n + 1, 0)), …, (a(0, p(n) + 1, 0)),
где 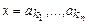
| |
| G5 | (Q(p(n), 0)) | |
| G6 | а) 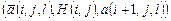 Замечание. Дизъюнкция гарантирует, что если головка машины в момент i не просматривает ячейку j, то в момент i + 1 ее содержимое не меняется
Замечание. Дизъюнкция гарантирует, что если головка машины в момент i не просматривает ячейку j, то в момент i + 1 ее содержимое не меняется
| 0 £ i £ p(n) ‑p(n) £ j £ p(n) + 1 0 £ l £ v |
б) 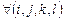
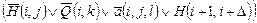
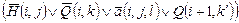
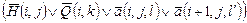 ,
где D, l, k’ определены командами машины:
если qk Î Q\{qY, qN}, то qk al à qk’ al’D;
если qk Î {qY, qN}, то D = 0, k’ = k, l’ = k ,
где D, l, k’ определены командами машины:
если qk Î Q\{qY, qN}, то qk al à qk’ al’D;
если qk Î {qY, qN}, то D = 0, k’ = k, l’ = k
| 0 £ i £ p(n) ‑p(n) £ j £ p(n) + 1 0 £ l £ v |
Заметим, что число дизъюнкций в G6 — полином от n. Далее, если x Î LП, то существует принимающее вычисление длины не большей p(n) и выполнимы все дизъюнкции из G1, G2, G3, G4, G5, G6, и x Î LП тогда и только тогда, когда существует выполняющий набор для fL = G1× G2× G3× G4× G5× G6. Теперь, для любого x Î LП индивидуальная задача fL(x) может быть построена за время, ограниченное полиномом от n = |x|, при этом длина fL(x) также ограничена сверху полиномом от n.
Таким образом, преобразование fL(x) может быть осуществлено за число действий, полиномиально зависящее от n. При этом fL(x) имеет O((p(n))2) переменных и O((p(n))2) дизъюнкций. Так как П — произвольная задача из NP, то тем самым теорема доказана.
18.3. Основные NP-полные задачи. Сильная NP-полнота
В данном разделе устанавливается NP-полнота некоторых известных в различных приложениях задач. Предпочтение отдается графическим задачам как наиболее наглядным. Доказательство получается преобразованием в рассматриваемую задачу другой задачи, NP-полнота которой установлена. Для задач с целочисленными параметрами вводится важное понятие – сильная NP-полнота.
1. Пусть f(x1, …, xn) — формула от булевых переменных x1, …, xn в конъюнктивной нормальной форме, где каждая дизъюнкция имеет не более, чем три вхождения переменных. Задача проверки выполнимости таких формул называется задачей 3-выполнимости (идентификатор: 3ВЫП).
Утверждение 18.6. Задача 3ВЫП является NP-полной.
Доказательство. Достаточно доказать, что ВЫПµ3ВЫП. Пусть F = D1D2 … Dm — индивидуальная задача выполнимость от переменных x1, …, xn. Пусть Di = z1 Ú z2 Ú … Ú zk и k > 3,  . Положим
. Положим
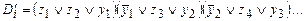
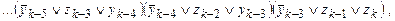
где y1, …, yk-3 — новые переменные. Покажем, что:
Di выполнено тогда и только тогда, когда существует значение y1, …, yk-3 такое, что 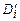 выполнено;
выполнено;
Di не выполнено тогда и только тогда, когда для любых значений y1, …, yk-3 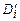 не выполнено.
не выполнено.
Действительно:
Di = 0 Þ z1 Ú z2 Ú … Ú zk = 0 Þ 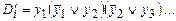
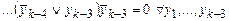 ;
;
Di = 1 Þ z1 Ú z2 Ú … Ú zk = 1 Þ 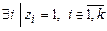 .
.
Укажем значения переменных y1, …, yk-3, выполняющие 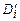 (табл.18.3).
(табл.18.3).
Таблица 18.3
| y1 | y2 | y3 | … | yk-3 | |
| z1 = 1 | … | ||||
| z2 = 1 | … | ||||
| z3 = 1 | … | ||||
| z4 = 1 | … | ||||
| … | … | … | … | … | … |
| zk = 1 | … |
Проделаем теперь процедуру замены каждой дизъюнкции Di на 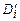 для каждого
для каждого  с условием k > 3. Получим задачу 3-выполнимости за полиномиальное время. По доказанному имеем ВЫПµ3ВЫП, что и требовалось доказать.
с условием k > 3. Получим задачу 3-выполнимости за полиномиальное время. По доказанному имеем ВЫПµ3ВЫП, что и требовалось доказать.
Замечание. Можно доказать, что задача 2-выполнимости лежит в классе P.
2. Рассмотрим графическую задачу (идентификатор: КЛИКА): по произвольному графу G(V, E) и числу k узнать, имеется ли в графе G полный (граф называется полным, если любые две вершины соединены ребром) подграф с k вершинами (клика).
Утверждение 18.7. Задача КЛИКА является NP-полной.
Доказательство. Ясно, что КЛИКА Î NP, так как словом-отгадкой для задачи служит список вершин, составляющих клику и детерминированный алгоритм за полиномиальное время проверяет наличие ребра между каждой парой вершин. Покажем, что ВЫП µ КЛИКА.
Пусть F = D1D2…Dm — произвольная индивидуальная задача ВЫП. Строим соответствующий граф GF следующим образом. Каждому вхождению переменной в F сопоставим вершину графа и присвоим ей обозначение (xa, i), где xa — вхождение переменного (a Î {0, 1}), i — номер соответствующей дизъюнкции. Вершины (xa, i) и (yb, j) соединим ребром в том и только в том случае, когда i ¹ j и xa не есть отрицание yb (т.е. x ¹ y или, если x = y, то a = b). Допустим, что F выполнима и пусть 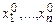 — соответствующий выполняющий набор. В каждом сомножителе F есть вхождение переменной, обратившее его в 1. Выберем по одному такому вхождению из каждой дизъюнкции. Рассмотрим соответствующее множество К вершин графа GF и покажем, что любые две такие вершины соединены ребром. Действительно, для вершин (xa, i) и (yb, j) нет соединяющего ребра лишь в случае i = j, либо
— соответствующий выполняющий набор. В каждом сомножителе F есть вхождение переменной, обратившее его в 1. Выберем по одному такому вхождению из каждой дизъюнкции. Рассмотрим соответствующее множество К вершин графа GF и покажем, что любые две такие вершины соединены ребром. Действительно, для вершин (xa, i) и (yb, j) нет соединяющего ребра лишь в случае i = j, либо 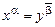 . Но x ¹ y, так как вхождения переменных взяты из разных дизъюнкций. Если
. Но x ¹ y, так как вхождения переменных взяты из разных дизъюнкций. Если 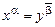 , то одно и то же значение переменного х не может одновременно обратить в 1 xa и yb. Значит, из выполнимости F следует наличие клики размера k в GF.
, то одно и то же значение переменного х не может одновременно обратить в 1 xa и yb. Значит, из выполнимости F следует наличие клики размера k в GF.
Обратно, пусть GF содержит клику размера k. Пусть это набор вершин 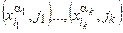 . Покажем, что формула F выполнима. Положим
. Покажем, что формула F выполнима. Положим 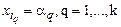 , и тогда
, и тогда 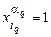 . Значения остальных переменных положим произвольно. Противоречия в выборе значений переменных нет, так как если
. Значения остальных переменных положим произвольно. Противоречия в выборе значений переменных нет, так как если 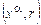 и
и 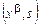 соединены ребром, то a = b.
соединены ребром, то a = b.
По построению GF вершинам соответствуют вхождения переменных из разных дизъюнкций и так как число вершин равно k, то каждая дизъюнкция имеет вхождение переменного, обращающего в 1 при данных значениях переменных, значит и F обращается в 1. Построение GF проводится за полиномиальное время и, следовательно, ВЫП µ КЛИКА, что и требовалось доказать.
3. Говорят, что некоторое множество вершин 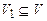 графа G(V, E) образует вершинное покрытие графа, если для любого ребра e Î E найдется инцидентная ему вершина v Î V1 этого множества. Задача о вершинном покрытии (идентификатор: ВП) состоит в том, чтобы по произвольному графу G(V, E) и числу К узнать, имеет ли граф вершинное покрытие мощности k.
графа G(V, E) образует вершинное покрытие графа, если для любого ребра e Î E найдется инцидентная ему вершина v Î V1 этого множества. Задача о вершинном покрытии (идентификатор: ВП) состоит в том, чтобы по произвольному графу G(V, E) и числу К узнать, имеет ли граф вершинное покрытие мощности k.
Утверждение 18.8. Задача ВП является NP-полной.
Доказательство. Ясно, что ВПÎNP, так как словом-догадкой является список вершин соответствующего вершинного покрытия и правильность ответа проверяется за полиномиальное время. Покажем, что КЛИКА µ ВП.
Для графа G(V, E) строим граф G’, являющийся дополнением G до полного графа (т.е. G’ = (V, E’)), где e Î E’ Û e Ï E). Покажем, что А есть полный подграф в G Û дополнение А’ = V\A есть ВП в G’.
Действительно, пусть полный подграф с множеством вершин А лежит в G. Тогда, если бы для ребра 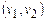 графа G’ выполнялось бы
графа G’ выполнялось бы











