Универсальные функции

Пусть F — некоторый класс функций от k переменных. Функцию U(n, x₁, …, x_k) от k + 1 переменных называют универсальной для класса F, если выполнимы условия:

а) для всякого n Î N₀ выполняется

f_n(x₁, …, x_k) = U(n, x₁, …, x_k) Î F;

б) для всякой f(x₁, …, x_k) Î F существует n Î N₀ такое, что f(x₁, …, x_k) = U(n, x₁, …, x_k).

Теорема 15.4. Для класса Ч¹ — одноместных частично рекурсивных функций существует универсальная частично рекурсивная функция U(n, x).

Доказательство. Определим U(n, x) = 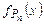, точнее

U(n, x) = 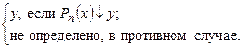(15.1)

Данное соотношение определяет частичную функцию. Функция U(n, x) является частично рекурсивной. Действительно, для произвольных (n, x) нужно найти программу P_n (эффективная процедура) и применить P_n к начальной конфигурации (x, 0, …, 0, …). Если P_n ¯, то положить U(n, x) = r₁, где r₁ — содержимое регистра R₁ в заключительной конфигурации. Если P_n ­, то считать значение U(n, x) неопределенным. По тезису Черча функция U(n, x) частично рекурсивна. Покажем, что функция U(n, x) универсальна. Поскольку U(n, x) частично рекурсивна, то и f_n = U(n, x) для всякого n Î N₀ частично рекурсивна, так как f_n получена подстановкой константы вместо первого аргумента. Пусть теперь f(x) — произвольная одноместная частично рекурсивная функция. Тогда по доказанному она может быть вычислена некоторой МПД-программой Р. Пусть n = g(P). Следовательно, f = 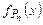и значит f = U(n, x), что и требовалось доказать.

Следствие 15.5. Для всякого k ³ 1 существует частично рекурсивная функция U^k(n, x₁, …, x_k) универсальная для всех k-местных частично рекурсивных функций.

Это делается с использованием нумерационных функций. Полагаем

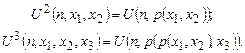
и так далее.

Покажем, например, что функция 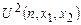удовлетворяет нужным условиям. Во-первых, функция U² — частично рекурсивна, так как является суперпозицией частично рекурсивных функций. Во-вторых, функция 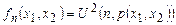частично рекурсивна, так как получается из частично рекурсивной подстановкой константы. Пусть теперь f(x₁, x₂) — произвольная частично рекурсивная функция. Образуем функцию g(x) = f(l(x), r(x)), где l, r — нумерационные функции. Так как g(x) — частично рекурсивна, то существует n такое, что g(x) = U(n, x). Теперь положим x = p(x₁, x₂), и тогда имеем

f(x₁, x₂) = g(p(x₁, x₂)) = U(n, p(x₁, x₂)) = ,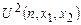

что и требовалось доказать.

Представляет интерес вопрос о существовании универсальной функции для других рассмотренных выше классов Ч₀ и Ч_пр — общерекурсивных и примитивно рекурсивных функций соответственно.

Теорема 15.6. Не существует общерекурсивной функции U^k(n, x₁, …, x_k), универсальной для класса Ч^k₀ — k-местных общерекурсивных функций при любом k ³ 1.

Доказательство. Пусть, наоборот, существует такая функция U^k(n, x₁, …, x_k) для некоторого k. Образуем функцию f(x₁, …, x_k) == U^k(x₁, x₁, …, x_k) + 1. Согласно свойству универсальности существует n₀ такое, что

U^k(n₀, x₁, …, x_k) = f(x₁, …, x_k) = U^k(x₁, x₁, …, x_k) + 1.

Поскольку данные функции всюду определены, то они определены и при x₁, x₁ = … = x_k = n₀. Тогда получаем противоречивое равенство U^k(n₀, n₀, …, n₀) = U^k(n₀, n₀, …, n₀) + 1. Значит, предположение о существовании универсальной функции ложно, что и требовалось доказать.

В то же время справедлива следующая теорема.

Теорема 15.7. Для каждого k Î N класс всех k-местных примитивно рекурсивных функций имеет общерекурсивную универсальную функцию.

Доказательство данной теоремы приведено в [11, § 5].

Заметим, что из данной теоремы следует, что класс общерекурсивных функций шире класса примитивно рекурсивных функций, так как универсальная функция не может быть примитивно рекурсивной и является общерекурсивной.

Дадим еще одно применение универсальной функции. Пусть f:N₀ à N₀ — частичная функция. Функцию f₀ будем называть доопределением f, если f₀ всюду определена и совпадает с f в ее области определения. Покажем, что рассмотрение частичных вычислимых функций вызвано существом дела, а именно — существуют частичные вычислимые функции, любое доопределение которых делает их невычислимыми.

Теорема 15.8. Существует частично рекурсивная функция f(x), которая не может быть доопределена до общерекурсивной.

Доказательство. Рассмотрим функцию f(x) = 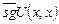, где U — универсальная функция. Данная фунция частично рекурсивна, так как она получается суперпозицией частично рекурсивных функций. Предположим, что существует общерекурсивная функция f₀(x), которая является доопределением для f(x). По свойству универсальности U существует n такое, что f₀(x) = U(n, x). Поскольку f₀(x) всюду определена, то она определена при x = n, и тогда значение U(n, n) определено, и, следовательно, определено значение 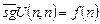. Поскольку f₀(x) есть доопределение f(x), то в области определения их значения должны совпадать. Поэтому имеем 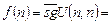U(n, n) = f₀(x). Однако последнее равенство дает противоречие, так как, если U(n, n) = 0, то 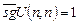, если U(n, n) ¹ 0, то 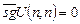. Значит, допущение о существовании рекурсивного доопределения для функции f(x) приводит к противоречию, что и требовалось доказать.

Л е к ц и я 16