Алгоритм на псевдокоде

ИСДП (L, R)

IF (L > R) ИСДП:=NIL

ELSE m : = [(L+R) / 2]

<Выделяем память для p>

p → Data : = A[m]

p → Left : = ИСДП ( L, m-1)

p → Right : = ИСДП ( m+1, R)

ИСДП:= p

FI

Для идеально сбалансированного дерева С_max = 2élog(n+1)ù. Если считать, что поиск любой вершины происходит одинаково часто, то ИСДП обеспечивает минимальное среднее время поиска. К существенным недостаткам ИСДП можно отнести то, что при добавлении нового элемента к множеству данных необходимо строить заново ИСДП.

10.3 Варианты заданий

1. Написать процедуру, определяющую является ли двоичное дерево деревом поиска. Проверить ее работу на двоичном дереве из предыдущего задания.

2. Запрограммировать процедуру поиска в дереве поиска элемента с заданным ключом и проверить ее работу на конкретном примере.

3. Определить количество операций, необходимых для поиска. Сравнить эту величину с высотой дерева.

4. Определить, что данное дерево является деревом поиска с помощью процедуры обхода дерева слева направо.

5. Определить, что данное дерево является деревом поиска с помощью процедур обхода дерева сверху вниз и снизу вверх.

6. Написать процедуру построения ИСДП из n элементов. Определить высоту построенного ИСДП и сравнить с теоретической оценкой.

7. Сделать поиск элемента в ИСДП. Сравнить количество операций, необходимых для поиска с высотой построенного ИСДП.

8. Графически изобразить ИСДП.

11. Случайное дерево поиска

11.1 Определение случайного дерева поиска

При решении многих типов задач объем данных заранее неизвестен, но необходима такая структура данных, для которой достаточно быстро выполняются операции поиска, добавления и удаления вершин. Одно из решений этой проблемы построение случайного дерева поиска(СДП). При построении СДП данные поступают последовательно в произвольном порядке и добавление нового элемента происходит в уже имеющееся дерево.

Пример случайного дерева поиска для последовательности D:

B 9 2 4 1 7 E F A D C 3 5 8 6

приведен на рисунке 32.

Рисунок 32 Случайное дерево поиска

Это дерево не является ИСДП. В худшем случае СДП может выродиться в список.

Пример. 1) D: 1 2 3 4 5 2) D: 5 1 2 4 3

Рисунок 33 Плохие СДП

Таким образом, средняя высота случайного дерева поиска может изменяться в пределах log n < h_{ср cд} < n при больших n. В [1] показано, что

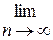( h_{ср сд} / h_{ср исдп}) = 2ln 2 = 1,386... и h_{ср сд} =О(log n) при n→∞.

11.2 Добавление вершины в дерево

Алгоритм добавления вершины в СДП заключается в следующем. Если дерево пустое, то создается корневая вершина, в которую записываются данные. В противном случае вершина добавляется к левому или правому поддереву в зависимости от результата сравнения с данными в текущей вершине.

При создании новой вершины нужно будет изменить значение указателя на нее, поэтому нам понадобиться указатель на указатель (двойная косвенность). На языках высокого уровня двойная косвенность обычно может быть реализована с помощью ссылки на указатель.

type pVertex = ^tVertex;

var p: ^pVertex;